安徽省安庆市桐城市2020届高三考试数学（理）试卷 9页

安徽省安庆市桐城市2020届高三考试数学（理）试卷 数学试卷（理）‎ 一、选择题（本大题共12小题，共60.0分）‎ 1. 已知集合，，若，则 A. B. C. D. ‎ 2. 若复数的对应点在直线上，则 A. B. C. D. 1‎ 3. 设等比数列的前6项和，且为，的等差中项，则 A. B. 8 C. 10 D. 14‎ ‎ ‎ 4. ‎2021年广东新高考将实行模式，即语文、数学、英语必选，物理、历史二选一，政治、地理、化学、生物四选二，共有12种选课模式．今年高一的小明与小芳都准备选历史，假若他们都对后面四科没有偏好，则他们选课相同的概率为       ‎ A. B. C. D. ‎ 5. 椭圆C：的左、右焦点分别为，，左右顶点分别为A，B，且，，点，，则的面积为 A. B. C. 1 D. 2‎ 6. 点P是所在平面上一点，若，则与的面积之比是 A. 3 B. 2 C. D. ‎ ‎ ‎ 7. 函数其中，的部分图象如图所示，将函数的图象向左平移个单位长度，得到的图象，则下列说法不正确的是 A. 函数为奇函数 B. 函数的最大值为3 C. 函数的最小正周期为 D. 函数在上单调递增 1. 设函数，则不等式的解集为 A. B. C. D. ‎ 2. 点D是直角斜边AB上一动点，，，将直角沿着CD翻折，使与构成直二面角，则翻折后的最小值是 A. B. C. D. ‎ 3. 设P为双曲线上且在一象限内的点，，分别是双曲的左、右焦点，，x轴上有一点A且，E是AP的中点，线段与交于点若，则双曲线的离心率是 A. B. C. D. ‎ 4. 已知函数有4个零点，则a的取值范围为 A. B. C. D. ‎ 5. 已知数列满足：，，其中为的前n项和．若对任意的n均有恒成立，则k的最大整数值为 A. 2 B. 3 C. 4 D. 5‎ 二、填空题（本大题共4小题，共20.0分）‎ 6. 的展开式中的常数项为______用数字作答 ‎ ‎ 7. 随机设置某交通路口亮红绿灯的时间，通过对路口交通情况的调查，确定相邻亮一次红灯与亮一次绿灯的时间之和为90秒，其中亮红灯的时间不超过60秒，亮绿灯的时间不超过50秒，则亮绿灯的时间不小于亮红灯的时间的概率为______．‎ 8. 在三棱锥中，，，，则三棱锥的外接球的表面积为______．‎ 9. 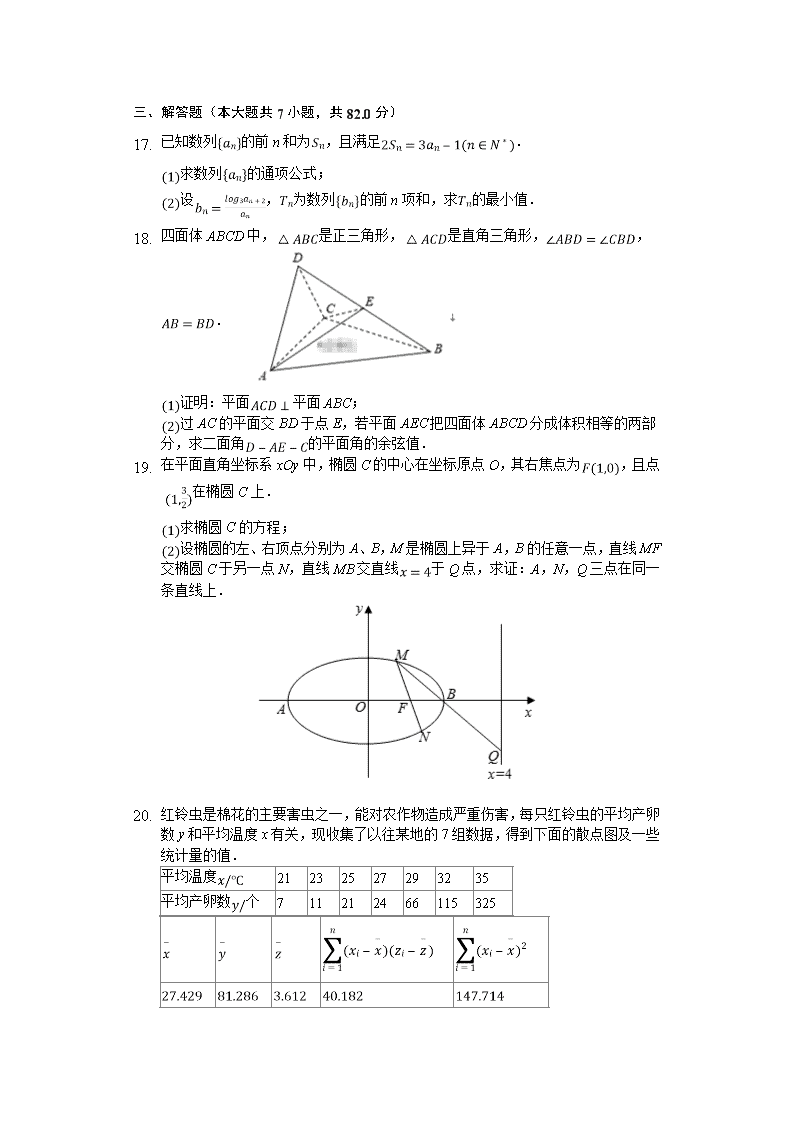已知平面四边形ABCD中，，，，，的面积为，则______．‎ ‎ ‎ 三、解答题（本大题共7小题，共82.0分）‎ 1. 已知数列的前n和为，且满足． 求数列的通项公式； 设，为数列的前n项和，求的最小值．‎ 2. 四面体ABCD中，是正三角形，是直角三角形，，．  证明：平面平面ABC； 过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角的平面角的余弦值．‎ 3. 在平面直角坐标系xOy中，椭圆C的中心在坐标原点O，其右焦点为，且点 在椭圆C上． 求椭圆C的方程； 设椭圆的左、右顶点分别为A、B，M是椭圆上异于A，B的任意一点，直线MF交椭圆C于另一点N，直线MB交直线于Q点，求证：A，N，Q三点在同一条直线上．‎ 4. 红铃虫是棉花的主要害虫之一，能对农作物造成严重伤害，每只红铃虫的平均产卵数y和平均温度x有关，现收集了以往某地的7组数据，得到下面的散点图及一些统计量的值．‎ 平均温度 ‎21‎ ‎23‎ ‎25‎ ‎27‎ ‎29‎ ‎32‎ ‎35‎ 平均产卵数个 ‎7‎ ‎11‎ ‎21‎ ‎24‎ ‎66‎ ‎115‎ ‎325‎ 表中 根据散点图判断，与其中为自然对数的底数哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型？给出判断即可，不必说明理由并由判断结果及表中数据，求出y关于x的回归方程．计算结果精确到小数点后第三位 根据以往统计，该地每年平均温度达到以上时红铃虫会造成严重伤害，需要人工防治，其他情况均不需要人工防治，记该地每年平均温度达到以上的概率为． 记该地今后5年中，恰好需要3次人工防治的概率为，求的最大值，并求出相应的概率． 当取最大值时，记该地今后5年中，需要人工防治的次数为X，求X的数学期望和方差．附：对于一组数据，，，其回归直线想斜率和截距的最小二乘法估计分别为：．‎ 1. 已知函数． 讨论的单调性； 设，若函数的两个极值点，恰为函数的两个零点，且的范围是，求实数a的取值范围．‎ 2. 以原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为a为常数，过点、倾斜角为的直线l的参数方程满足，为参数． 求曲线C的普通方程和直线l的参数方程； 若直线l与曲线C相交于A、B两点点P在A、B之间，且，求a和的值．‎ 3. 设函数，． 当时，求不等式的解集； 若关于x的不等式有解，求a的取值范围．‎ 高三数学试卷（理）‎ 一、选择题（本大题共12小题，共60.0分）‎ ACBDC DDBBA AB 二、填空题（本大题共4小题，共20.0分）‎ ‎13【答案】180 14【答案】 15【答案】 16【答案】2‎ 三、解答题（本大题共7小题，共82.0分）‎ ‎17【答案】解：． 时，，化为：， 时，，解得． 数列是等比数列，首项为1，公比为3， ． ，， 数列的前n项和． ， ， 化为：． 的最小值是．‎ ‎18【答案】证明：取AC的中点O，连接BO，OD． 是等边三角形，． 与中，，，， ≌，， 是直角三角形， 是斜边，． ， ， ， ， 又，平面ACD，平面ACD， 平面ACD， 又平面ABC， 平面平面ABC． 解：设点D，B到平面ACE的距离分别为，则， 平面AEC把四面体ABCD分成体积相等的两部分， ． 点E是BD 的中点． 建立如图所示的空间直角坐标系． 不妨取， 则0，，0，，0，，0，，，， 0，，，0，， 设平面ADE的法向量为y，， 则，即，取， 同理可得，平面ACE的法向量为1，， 由图可知此二面角的平面角为锐角， 二面角的平面角的余弦值为．‎ ‎19【答案】解：不妨设椭圆的方程为，， 由题意可得，解得，， 故椭圆的方程， 证明：设，，直线MN的方程为， 由方程组，消去x整理得 ，， 直线BM的方程可表示为， 将此方程与直线成立，可求得点Q的坐标为， ，， ‎ ‎， ， 向量和有公共点A， ，N，Q三点在同一条直线上．‎ ‎20【答案】解：根据散点图可以判断， 更适宜作为平均产卵数y关于平均温度x的回归方程类型； 对两边取自然对数，得； 令，，，得； 因为， ； 所以z关于x的回归方程为； 所以y关于x的回归方程为； 由，得， 因为，令，得，解得； 所以在上单调递增，在上单调递减， 所以有唯一的极大值为，也是最大值； 所以当时，； 由知，当取最大值时，， 所以， 所以X的数学期望为， 方差为．‎ ‎21【答案】解：的定义域为，． 若，则，当且仅当，时，， 若，令得，． 当时，； 当时，， 所以，当时，单调递减区间为，无单调递增区间； 当时，单调递减区间为，‎ ‎；单调递增区间为 由知：且，． 又， ， 由得 ． 令， ， ， 所以y在上单调递减． 由y的取值范围是，得t的取值范围是， ， ， 又， 故实数a的取值范围是．‎ ‎22【答案】解：由得，--------------------------------------分 又，，得， 的普通方程为，-------------------------------------------------------------------分 过点、倾斜角为的直线l的普通方程为，--------------分 由得 直线l的参数方程为为参数；-------------------------------------------分 将代入， 得，----------------------------------------------------------------‎ 分 依题意知 则上方程的根、就是交点A、B对应的参数，， 由参数t的几何意义知，得， 点P在A、B之间，， ，即，解得满足，，-------------分 ，又， -------------------------------------------------------------------------分 ‎23【答案】解：当时，，即， 即或或， 所以或， 所以原不等式的解集为； ， 因为不等式有解， 所以，即， 所以a的取值范围是．‎