专题8-5+直线、平面垂直的判定与性质（测）-2018年高考数学一轮复习讲练测（浙江版） 18页

‎2018年高考数学讲练测【浙江版】【测】第八章 立体几何 第05节 直线、平面垂直的判定与性质 班级__________ 姓名_____________ 学号___________ 得分__________‎ 一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的。）‎ ‎1．【2017届浙江省杭州市高三4月】设， 是两个不同的平面， 是一条直线，给出下列命题：‎ ‎①若， ，则；②若， ，则.则（ ）‎ A. ①②都是假命题 B. ①是真命题，②是假命题 C. ①是假命题，②是真命题 D. ①②都是真命题 ‎【答案】B ‎2．【2017届浙江省湖州、衢州、丽水三市高三4月联考】已知平面与两条不重合的直线，则“，且”是“”的( )‎ A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 ‎【答案】A ‎【解析】若，则必有，但时，直线与平面可以平行，可以相交，可以在平面内，不一定垂直，因此“”是“”的充分不必要条件，故选A．‎ ‎3．【2016届浙江省宁波市高三上学期期末】如图，在正方形ABCD中，点E,F分别为边BC,AD的中点，将‎△ABF沿BF所在直线进行翻折，将‎△CDE沿DE所在直线进行翻折，在翻折过程中（ ）‎ A. 点A与点C在某一位置可能重合 B. 点A与点C的最大距离为‎3‎AB C. 直线AB与直线CD可能垂直 D. 直线AF与直线CE可能垂直 ‎【答案】D ‎4．【2016届浙江省宁波市高三上学期期末】已知m,n是两条不同的直线，α,β,γ是三个不同平面，下列命题中正确的是（ ）‎ A. 若m⊥α，m⊥β，则α⊥β B. 若α⊥γ，β⊥γ，则α//β C. 若m//α，m//β，则α//β D. 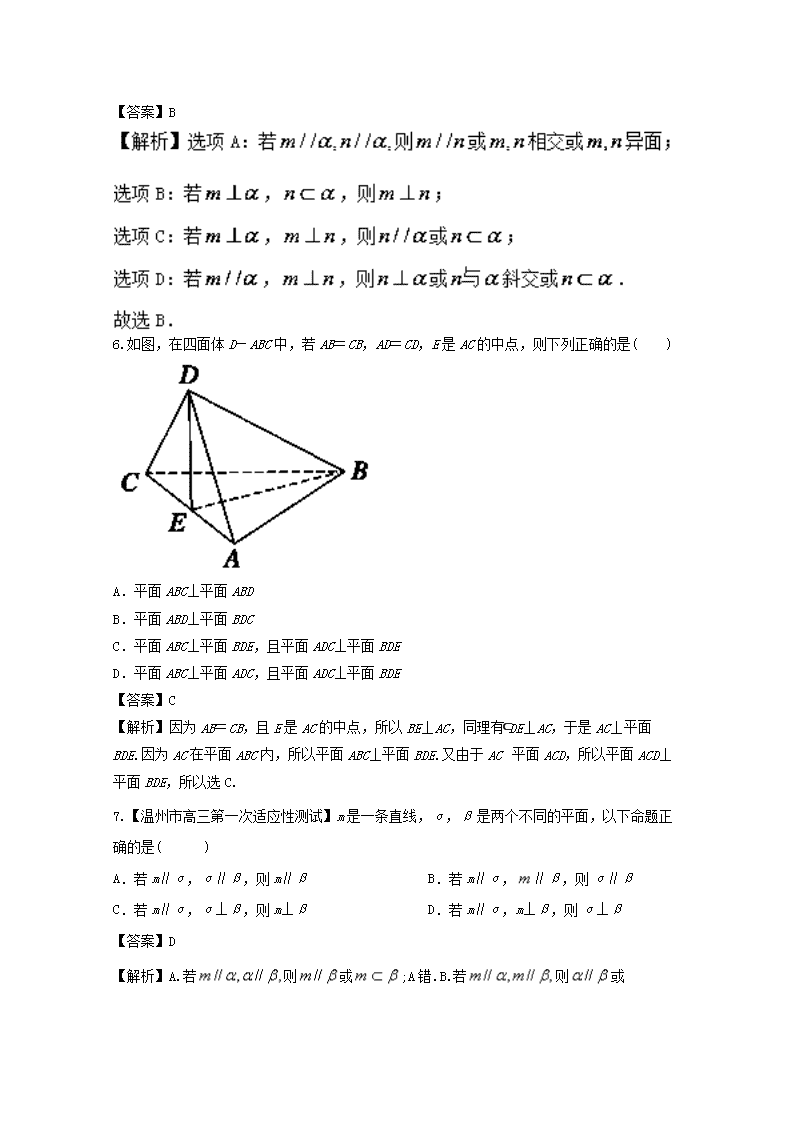m⊥α若，n//α，则m⊥n ‎【答案】D ‎【解析】‎ A‎ 不正确，因为垂直于同一条直线的两个平面平行；B 不正确，垂直于同一个平面的两个平面平行或相交；C 平行于同一条直线的两个平面平行或相交；D正确.‎ ‎5．已知表示两条不同直线，表示平面，下列说法正确的是（ ） ‎ A．若则 ‎ B．若，，则 C．若，，则 ‎ D．若，，则 ‎【答案】B ‎6.如图，在四面体D－ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列正确的是(　　)‎ A．平面ABC⊥平面ABD B．平面ABD⊥平面BDC C．平面ABC⊥平面BDE，且平面ADC⊥平面BDE D．平面ABC⊥平面ADC，且平面ADC⊥平面BDE ‎【答案】C ‎【解析】因为AB＝CB，且E是AC的中点，所以BE⊥AC，同理有DE⊥AC，于是AC⊥平面BDE.因为AC在平面ABC内，所以平面ABC⊥平面BDE.又由于AC⊂平面ACD，所以平面ACD⊥平面BDE，所以选C.‎ ‎7.【温州市高三第一次适应性测试】m是一条直线，α，β是两个不同的平面，以下命题正确的是( )‎ A．若m∥α，α∥β，则m∥β B．若m∥α，∥β，则α∥β ‎ C．若m∥α，α⊥β，则m⊥β D．若m∥α，m⊥β，则α⊥β ‎【答案】D ‎【解析】A.若则或;A错.B.若则或 B错；‎ C.若则或或C错;D. 存在直线，使,,又，故选D.‎ ‎8.【浙江省“六市六校”联盟高考模拟考试】空间中，设表示直线，， 表示不同的平面，则下列命题正确的是（ ）‎ A.若，，则 B . 若，，则 C.若，，则 D. 若，，则 ‎【答案】B ‎【解析】若，，则或，故A错；若，，则和的位置关系不确定，故C错；若，，则或，故D错，选B．‎ ‎9.设是两条不同的直线，是三个不同的平面，下列四个命题中假命题的是( ) ‎ A.若则　　 B.若则 C.若则　　　 D.若，则 ‎【答案】C ‎10.下列四个命题中，正确命题的个数是( )个 ‎① 若平面平面，直线平面，则；‎ ‎② 若平面平面，且平面平面，则；‎ ‎③ 平面平面，且，点，，若直线，则；‎ ‎④ 直线为异面直线，且平面，平面，若，则. ‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】A答案：如果加入条件，则；‎ B答案：例如墙角的三个面，则；‎ C答案：如果加入条件，则；‎ D答案：从向量角度看，与分别是的法向量，显然，即.‎ 所以只有D正确.‎ ‎11.【2017届浙江省温州市二模】已知空间两不同直线m、n，两不同平面α，β，下列命题正确的是（ ）‎ A. 若m∥α且n∥α，则m∥n B. 若m⊥β且m⊥n，则n∥β C. 若m⊥α且m∥β，则α⊥β D. 若m不垂直于α，且n⊂α，则m不垂直于n ‎【答案】C ‎12.如图，ABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎为正方体，下面结论：①BD∥‎平面CB‎1‎D‎1‎；②AC‎1‎⊥BD；③AC‎1‎⊥‎平面CB‎1‎D‎1‎；④直线B‎1‎D‎1‎与BC所成的角为45°．其中正确结论的个数是( )‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】D ‎【解析】‎ 由正方体的性质得，BD//‎B‎1‎D‎1‎ ，所以，BD//‎ 平面CB‎1‎D‎1‎ ，故①正确．由正方体的性质得AC⊥BD ，而AC 是AC‎1‎ 在底面ABCD 内的射影，由三垂线定理知， AC‎1‎⊥BD，故②正确．由正方体的性质得BD//‎B‎1‎D‎1‎ ，由②知，AC‎1‎⊥BD ，所以，AC‎1‎⊥‎B‎1‎D‎1‎ ，同理可证AC‎1‎⊥CB‎1‎ ，故AC‎1‎ 垂直于平面CB‎1‎D‎1‎ 内的两条相交直线，所以，AC‎1‎ ⊥平面CB‎1‎D‎1‎ ，故③正确．异面直线B‎1‎D‎1‎与BC所成的角就是直线BC 与BD 所成的角，故‎∠CBD 为异面直线B‎1‎D‎1‎与BC所成的角，在等腰直角三角形BCD 中，‎∠CBD=45°‎ ，故④正确．‎ 二、填空题（本大题共4小题，每小题5分，共20分。把答案填在题中的横线上.）‎ ‎13.【2018届安徽省屯溪第一中学高三第二次月考】已知在直角梯形ABCD中，AB⊥AD,CD⊥AD,AB=2AD=2CD=2‎,将直角梯形ABCD沿AC折叠成三棱锥D-ABC，当三棱锥D-ABC的体积取最大值时，其外接球的体积为__________．‎ ‎【答案】‎4π‎3‎ ‎4π‎3‎ ；‎ ‎【解析】如图：AB=2,AD=1,CD=1‎，∴ ‎AC=‎2‎,BC=‎‎2‎ ‎∴ BC⊥AC，‎ 取AC的中点E，AB的中点O，连结DE，OE，‎ 取AC的中点E，AB的中点O，连结DE，OE， ∵三棱锥体积最大时， ∴平面DCA⊥平面ACB， ∴OB=OA=OC=OD， ∴OB=1，就是外接球的半径为1， 此时三棱锥外接球的体积：‎4π‎3‎‎×‎1‎‎3‎=‎‎4π‎3‎．‎ ‎14.【2018届河北省邢台市高三上学期第一次月考】在中， ， ， ，点分别在边上，且，沿着将折起至的位置，使得平面平面，其中点为点翻折后对应的点，则当四棱锥的体积取得最大值时， 的长为__________.‎ ‎【答案】‎ 当时， 单调递增；‎ 当时， 单调递减；‎ 故当时， 取得最大值.‎ ‎15. 如图，PA⊥圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E、F分别是点A在PB、PC上的正投影，给出下列结论：‎ ‎①AF⊥PB；②EF⊥PB；‎ ‎③AF⊥BC；④AE⊥平面PBC.‎ 其中正确结论的序号是________．‎ ‎【答案】①②③‎ ‎16.【2017届湖北省武汉市武昌区高三1月调研】在矩形ABCD中，ABBC，这与已知矛盾，所以③不正确.‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. （本题满分10分）【2018届河南省中原名校高三第三次质量考评】如图，在四棱锥中， ， ， ，平面底面， ， 和分别是和的中点．　‎ ‎（1）求证： 平面；‎ ‎（2）求证：平面平面．‎ ‎【答案】（1）见解析（2）见解析 试题解析：‎ ‎（1）∵， ， 是的中点，‎ ‎∴，且，‎ ‎∴为平行四边形，‎ ‎∴，‎ ‎∴平面．‎ ‎（2）∵且为平行四边形，‎ ‎∴， ，‎ 由已知可得底面，‎ ‎∴，∴平面，∴，‎ ‎∵和分别是和的中点，∴，∴，‎ ‎∴平面，∴平面 平面．‎ ‎18．（本题满分12分）【2018届湖北省宜昌市葛洲坝中学高三9月月考】在如图所示的正方体ABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎中，‎ ‎（1）过点C作与面A‎1‎BD平行的截面；‎ ‎（2）求证：‎AC‎1‎⊥面A‎1‎BD ‎（3）若正方体的棱长为2，求四面体A‎1‎BC‎1‎D的体积。‎ ‎【答案】（1）见解析；（2）见解析；（3）.‎ 试题解析：‎ ‎(1)见下图 ‎ ‎ ‎(2)证明： 正方体ABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎， CC‎1‎⊥面ABCD ‎‎∴CC‎1‎⊥BD 又有 AC⊥BD‎,‎∴BD⊥面ACC‎1‎A‎1‎,‎‎∵AC‎1‎⊂面ACC‎1‎A‎1‎，∴BD⊥AC‎1‎ 同理AC‎1‎⊥A‎1‎B,而BD∩A‎1‎B=B,‎∴AC‎1‎⊥面A‎1‎BD。‎ ‎(3)法一（直接计算）由（2）知AC‎1‎⊥面A‎1‎BD，设垂足为O,由等积法知AO=‎2‎‎3‎‎3‎,∴C‎1‎O=‎‎4‎‎3‎‎3‎ ‎∴VA‎1‎BC‎1‎D=‎1‎‎3‎SΔA‎1‎BD·C‎1‎O=‎1‎‎3‎⋅‎3‎‎4‎⋅‎2‎‎2‎‎2‎⋅‎4‎‎3‎‎3‎=‎‎8‎‎3‎‎ ‎ 法二：（间接计算）用正方体体积减去四个角落的体积 ‎19.（本题满分12分）如图所示，在三棱柱中，平面ABC，AB⊥AC.‎ ‎（1）求证：；‎ ‎（2）若P是棱的中点，求平面PAB将三棱柱分成的两部分体积之比.‎ ‎【答案】（1）证明见解析；（2）.‎ ‎【解析】‎ 试题分析：（1）先证平面⊥平面，再由面面垂直的性质定理得平面，进而得；（2）将棱台还原为棱锥，可求得，进而可得两部分体积比 .‎ ‎（2）设平面PAB与棱交于点Q.因为P为棱的中点，所以Q为棱的中点，连接AQ，PQ.‎ 设三棱柱的底面积为S，高为h，体积为V，则Sh=V。‎ 如图将棱台还原为棱锥，可求得.‎ 所以.所以.‎ ‎20. （本题满分12分）如图，直三棱柱中，，分别是棱的中点，点在棱上，已知.‎ ‎（1）求证：平面；‎ ‎（2）设点在棱上，当为何值时，平面平面.‎ ‎【答案】(1)证明见解析；(2).‎ 因为平面, 平面，所以平面…………………………6分 ‎（2）解：当时，平面平面.…………………………7分 因为，故…………………………8分 在直三棱柱中，平面, 平面,故平面平面.又平面平面,平面，平面,故.‎ 又故.…………………………10分 易证与相交，‎ 故平面.‎ 又平面，故平面平面.…………………………12分 ‎ ‎21. （本题满分12分）【2018届河南省郑州市第一中学高三上学期第二次月考】在四棱锥 中，底面是矩形， 平面， 是等腰三角形， ， 是的一个三等分点（靠近点），的延长线与的延长线交于点，连接．‎ ‎（1）求证： ；‎ ‎（2）求证：在线段上可以分别找到两点， ，使得直线平面，并分别求出此时的值．‎ ‎【答案】(1)见解析；(2)证明见解析， ， .‎ 试题解析：‎ ‎（1）证明：因为平面， 平面，所以.‎ 因为底面是矩形，所以 又因为，所以平面.‎ 又因为平面，所以.‎ ‎（2）如图所示，取线段的中点，连接，‎ 作，垂足为，连接，则此时满足直线平面.‎ 由（1）得， 平面，又平面，‎ 所以 ‎ 因为平面，所以 又因为是等腰三角形，所以.‎ 又因为，所以平面.‎ 又因为， ，所以平面.‎ 易知，下面求解：‎ 因为， ，所以可设，则， .‎ 在等腰直角三角形中，由勾股定理，得.‎ 因为平面，又平面，‎ 所以 的平面图如图所示：‎ 在中，由勾股定理，得，‎ 所以.‎ 在中，由，得所以.‎ 综上，在线段上可以分别找到两点， ，使得直线平面，‎ 并且此时， ‎ ‎22.（本题满分12分）【四川卷】在如图所示的多面体中，四边形和都为矩形。‎ ‎ （Ⅰ）若，证明：直线平面；‎ ‎ （Ⅱ）设，分别是线段，的中点，在线段上是否存在一点，使直线平面？请证明你的结论。‎ ‎【答案】（1）证明见解析；（2）存在一点（线段的中点），使直线平面．.‎ ‎（Ⅱ）取线段的中点，连接，，，，设为，的交点．‎ 由已知，为的中点．‎ 连接，，则，分别为，的中位线，‎ 所以，，‎ 因此，．‎ 连接，从而四边形为平行四边形，则．‎ 因为直线平面，平面．‎ 所以直线平面．‎ 即线段上存在一点（线段的中点），使直线平面．‎ ‎ ‎