- 946.22 KB
- 2021-06-02 发布
真题回放
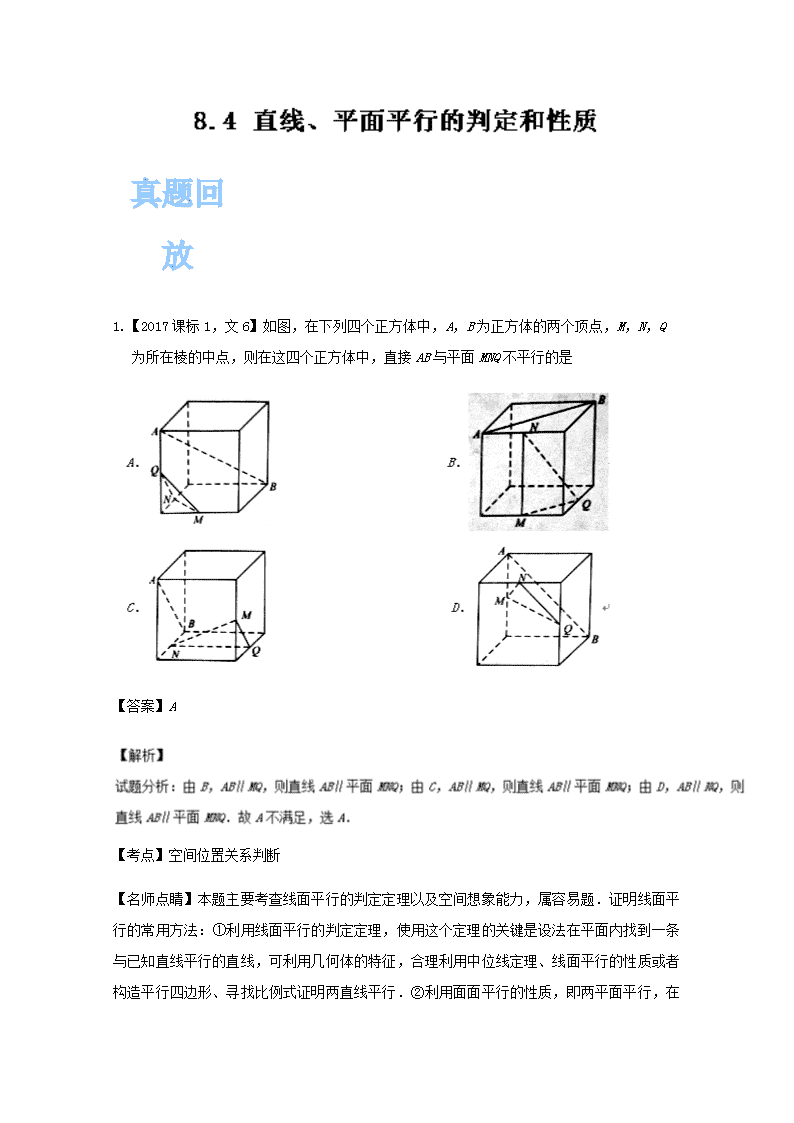
1.【2017课标1,文6】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是
【答案】A
【考点】空间位置关系判断
【名师点睛】本题主要考查线面平行的判定定理以及空间想象能力,属容易题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②
利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面.
2.【2015高考浙江,文4】设,是两个不同的平面,,是两条不同的直线,且,( )
A.若,则 B.若,则
C.若,则 D.若,则
【答案】A
【解析】采用排除法,选项A中,平面与平面垂直的判定,故正确;选项B中,当时,可以垂直,也可以平行,也可以异面;选项C中,时,可以相交;选项D中,时,也可以异面.故选A.
【考点定位】直线、平面的位置关系.
【名师点睛】本题主要考查空间直线、平面的位置关系.解答本题时要根据空间直线、平面的位置关系,从定理、公理以及排除法等角度,对个选项的结论进行确认真假.本题属于容易题,重点考查学生的空间想象能力以及排除错误结论的能力.
3. 【2017江苏,15】 如图,在三棱锥A-BCD中,AB⊥AD, BC⊥BD, 平面ABD⊥平面BCD, 点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.
求证: EF∥平面ABC;
【答案】见解析
4.【2017山东,文18】由四棱柱ABCD-A1B1C1D1截去三棱锥C1- B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E平面ABCD,
(Ⅰ)证明:∥平面B1CD1;
【答案】①证明见解析.
【解析】
试题分析:(Ⅰ)取中点,证明,(Ⅱ)证明面.
【考点】空间中的线面位置关系
5. 【2016高考山东文数】在如图所示的几何体中,D是AC的中点,EF∥DB.
(I)已知AB=BC,AE=EC.求证:AC⊥FB;
(II)已知G,H分别是EC和FB的中点.求证:GH∥平面ABC.
【答案】(Ⅰ))证明:见解析;(Ⅱ)见解析.
【解析】
考点分析
考点
了解A
掌握B
灵活运用C
直线与平面平行的判定及性质
B
高考对这部分的考查主要集中在以下几个方面:1、常融合平行、垂直等多种关系于一体考察,以选择题居多;2、直接考查证明直线与平面平行,常在解答题中的第一问考查;3、以线面平行的探讨性问题居多,一般以是否存在某定点的形式考察,常在解答题中的第二问考查。
知识链接
1.线面平行的判定定理和性质定理
文字语言
图形语言
符号语言
判定定理
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行(简记为“线线平行⇒线面平行”)
∵l∥a,a⊂α,l⊄α,∴l∥α
性质定理
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)
∵l∥α,l⊂β,α∩β=b,∴l∥b
2.面面平行的判定定理和性质定理
文字语言
图形语言
符号语言
判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)
∵a∥β,b∥β,a∩b=P,a⊂α,b⊂α,∴α∥β
性质定理
如果两个平行平面同时和第三个平面相交,那么它们的交线平行
∵α∥β,α∩γ=a,β∩γ=b,∴a∥b
【知识拓展】
重要结论:
(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β;
(2)垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b;
(3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.
融会贯通
题型一 直线与平面平行的判定与性质
命题点1 直线与平面平行的判定
例1 如图,四棱锥P-ABCD中,AD∥BC,AB=BC=AD,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.
(1)求证:AP∥平面BEF;
(2)求证:GH∥平面PAD.
【答案】详见解析
命题点2 直线与平面平行的性质
例2 (2017·长沙调研)如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥
平面GEFH.
(1)证明:GH∥EF;
(2)若EB=2,求四边形GEFH的面积.
【答案】详见解析
由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,
从而KB=DB=OB,即K为OB的中点.
再由PO∥GK得GK=PO,
即G是PB的中点,且GH=BC=4.
由已知可得OB=4,
PO===6,
所以GK=3.
故四边形GEFH的面积S=·GK
=×3=18.
解题技巧与方法总结
判断或证明线面平行的常用方法
(1)利用线面平行的定义(无公共点);
(2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α);
(3)利用面面平行的性质定理(α∥β,a⊂α⇒a∥β);
(4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).
【变式训练】如图所示,CD,AB均与平面EFGH平行,E,F,G,H分别在BD,BC,AC,AD上,且CD⊥AB.求证:四边形EFGH是矩形.
【答案】详见解析
题型二 平面与平面平行的判定与性质
例3 如图所示,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
(1)B,C,H,G四点共面;
(2)平面EFA1∥平面BCHG.
【答案】详见解析
【解析】证明 (1)∵G,H分别是A1B1,A1C1的中点,
∴GH是△A1B1C1的中位线,
∴GH∥B1C1.
又∵B1C1∥BC,
∴GH∥BC,
∴B,C,H,G四点共面.
∴平面EFA1∥平面BCHG.
引申探究
1.在本例条件下,若D为BC1的中点,求证:HD∥平面A1B1BA.
【答案】详见解析
【解析】证明 如图所示,连接HD,A1B,
∵D为BC1的中点,H为A1C1的中点,
∴HD∥A1B,
又HD⊄平面A1B1BA,
A1B⊂平面A1B1BA,
∴HD∥平面A1B1BA.
2.在本例条件下,若D1,D分别为B1C1,BC的中点,求证:平面A1BD1∥平面AC1D.
【答案】详见解析
【解析】证明 如图所示,连接A1C交AC1于点M,
解题技巧与方法总结
证明面面平行的方法
(1)面面平行的定义;
(2)面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行;
(3)利用垂直于同一条直线的两个平面平行;
(4)两个平面同时平行于第三个平面,那么这两个平面平行;
(5)利用“线线平行”、“线面平行”、“面面平行”的相互转化.
【变式训练】(2016·许昌三校第三次考试)如图所示,四边形ABCD与四边形ADEF都为平行四边形,M,N,G分别是AB,AD,EF的中点.求证:
(1)BE∥平面DMF;
(2)平面BDE∥平面MNG.
【答案】详见解析
题型三 平行关系的综合应用
例4 如图所示,在三棱柱ABC-A1B1C1中,D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,请确定点E的位置;若不存在,请说明理由.
【答案】详见解析
【解析】 方法一 存在点E,且E为AB的中点时,DE∥平面AB1C1.
下面给出证明:
如图,取BB1的中点F,连接DF,
则DF∥B1C1,
∵AB的中点为E,连接EF,ED,
则EF∥AB1,B1C1∩AB1=B1,
∴平面DEF∥平面AB1C1.
而DE⊂平面DEF,
∴DE∥平面AB1C1.
方法二 假设在棱AB上存在点E,
使得DE∥平面AB1C1,
解题技巧与方法总结
利用线面平行的性质,可以实现与线线平行的转化,尤其在截面图的画法中,常用来确定交线的位置,对于最值问题,常用函数思想来解决.
【变式训练】如图所示,在四面体ABCD中,截面EFGH平行于对棱AB和CD,试问截面在什么位置时其截面面积最大?
【答案】详见解析
即当截面EFGH的顶点E、F、G、H分别为棱AD、AC、BC、BD的中点时截面面积最大.
练习检测
1.(福建省2017年数学基地校高三毕业班总复习形成性试卷(文))如图, 平面 平面,过, 的直线, 分别交、于、于 , 和, ,若, , ,则的长为( )
A. B. C. D.
【答案】C
【解析】选C.由易证
即,
故选C.
2.(2017届山西省高三3月高考考前适应性测试)在三棱柱中, , , 为的中点.
(1)证明: 平面;
(2)若,点在平面的射影在上,且侧面的面积为,求三棱锥的体积.
【答案】(1)见解析;(2).
试题解析:
(1)证明:连接交于点,连接.
则为的中点,又为的中点,所以,且平面, 平面,则平面.
(2)解:取的中点,连接,过点作于点,连接.
因为点在平面的射影在上,且,
所以平面,∴, ,∴平面,
则.
3.(宁夏石嘴山市第三中学2017届高三下学期第三次模拟)如图: 是平行四边行, 平面, // , , , 。
(1)求证: //平面;
【答案】(1)证明见解析
【解析】试题分析:证明线面平行有两种思路,利用判定定理寻求线线平行或利用面面平行,本题利用判定定理去证明,取 的中点,连接,证明四边形为平行四边形,进而得出线线平行,证明出线面平行;第二步证明面面平行,只需证明一个平面内的一条直线与另一个平面垂直, 成为最佳选择,所以围绕证明直线平面展开.
4.(2017届江西省南昌市高三第一次模拟)如图,四棱锥中,平面平面,底面为梯形, , ,,且与均为正三角形, 为的中点, 为重心.
(1)求证: 平面;
(2)求三棱锥的体积.
【答案】(Ⅰ)详见解析(Ⅱ)
试题解析:(Ⅰ)方法一:连交于,连接.
由梯形,且,知
又为的中点,为的重心,∴
在中, ,故// .
又平面, 平面,∴//平面.
方法二:过作交于,过作交于,连接,
为的重心,,,
又为梯形,,,
, ∴
又由所作,得// ,为平行四边形.
,面
(Ⅱ) 方法一:由平面平面, 与均为正三角形, 为的中点
∴, ,得平面,且
由(Ⅰ)知//平面,∴
又由梯形,,且,知
又为正三角形,得,∴,
得
∴三棱锥的体积为.
方法二: 由平面平面, 与均为正三角形, 为的中点
∴, ,得平面,且
由,∴
而又为正三角形,得,得.
∴,∴三棱锥的体积为.
点睛:本题主要考查,线面间垂直的性质与判定,三棱锥的体积,空间想象能力,推理论证能力.在计算柱,锥,台的体积关键是根据条件找出相应的底面积和高.如果给出的几何体不规则 ,需要利用求体积的一些特殊方法:分割法,补体法,转化法等,它们是解决一些不规则几何体体积计算常用的方法,选择,填空题中使用居多,要熟练掌握.本题使用转化法,将底和高进行转化.
5.(天津市河东区2017届高三二模)如图,在四棱锥中, 平面,
,且, , , 为线段上一点, ,且为的中点.
(Ⅰ)证明: 平面;
【答案】(1)见解析
6.(吉林省吉林大学附属中学2017届高三第六次摸底)如图,三棱柱中,侧棱与底面垂直, , , 分别是的中点.
(Ⅰ)证明: 平面;
(Ⅱ)求三棱锥的体积.
【答案】(Ⅰ)平面 (Ⅱ)三棱锥的体积为
【解析】
(Ⅱ)
∵三棱锥的体积,
∵, ,∴,
又, ,∴平面,
∴,
∴三棱锥的体积为.
7.(河北省武邑中学2017届高三下学期第四次模拟)在四棱锥中, , , 是的中点,面面.
(Ⅰ)证明: 面;
【答案】(1)详见解析;
8.(云南省民族中学2017届高三适应性考试)如下图,在四棱锥中,底面是边长为的正方形,平面平面, , 为中点,且.
(Ⅰ)求证: 平面;
【答案】(Ⅰ)见解析;