2018-2019学年河南省驻马店市高一下学期期末考试数学（文）试题（解析版） 17页

‎2018-2019学年河南省驻马店市高一下学期期末考试数学（文）试题 一、单选题 ‎1．的值等于( )‎ A． B． C． D．‎ ‎【答案】A ‎【解析】= ,选A.‎ ‎2．已知在中，，且，则的值为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】先确定D位置，根据向量的三角形法则，将用，表示出来得到答案.‎ ‎【详解】‎ ‎ ‎ 故答案选C ‎【点睛】‎ 本题考查了向量的加减，没有注意向量方向是容易犯的错误.‎ ‎3．某单位共有老、中、青职工430人，其中有青年职工160人，中年职工人数是老年职工人数的2倍．为了解职工身体状况，现采用分层抽样方法进行调查，在抽取的样本中有青年职工32人，则该样本中的老年职工人数为( )‎ A．9 B．18 C．27 D．36‎ ‎【答案】B ‎【解析】试题分析：‎ 根据条件中职工总数和青年职工人数，以及中年和老年职工的关系列出方程，解出老年职工的人数，根据青年职工在样本中的个数，算出每个个体被抽到的概率，用概率乘以老年职工的个数，得到结果．‎ 设老年职工有x人，中年职工人数是老年职工人数的2倍，则中年职工有2x，∵x+2x+160=430，∴x=90，即由比例可得该单位老年职工共有90人，∵在抽取的样本中有青年职工32人，∴每个个体被抽到的概率是 用分层抽样的比例应抽取×90=18人．故选B．‎ ‎【考点】分层抽样 点评：本题是一个分层抽样问题，容易出错的是不理解分层抽样的含义或与其它混淆．抽样方法是数学中的一个小知识点，但一般不难，故也是一个重要的得分点，不容错过 ‎4．计算：的结果为（ ）‎ A．1 B．2 C．-1 D．-2‎ ‎【答案】B ‎【解析】利用恒等变换公式化简得的答案.‎ ‎【详解】‎ 故答案选B ‎【点睛】‎ 本题考查了三角恒等变换，意在考查学生的计算能力.‎ ‎5．已知平面向量满足：，，，若，则的值为（ ）‎ A． B． C．1 D．-1‎ ‎【答案】C ‎【解析】将代入，化简得到答案.‎ ‎【详解】‎ 故答案选C ‎【点睛】‎ 本题考查了向量的运算，意在考查学生的计算能力.‎ ‎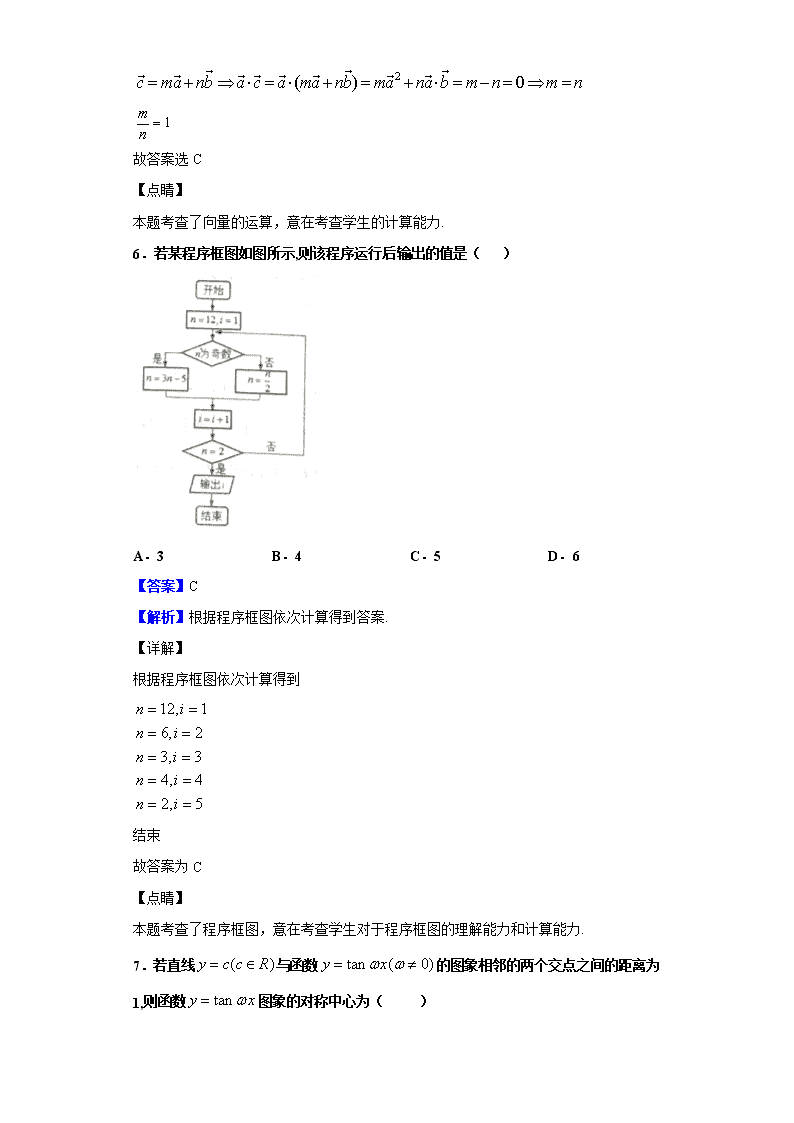6．若某程序框图如图所示,则该程序运行后输出的值是（ ）‎ A．3 B．4 C．5 D．6‎ ‎【答案】C ‎【解析】根据程序框图依次计算得到答案.‎ ‎【详解】‎ 根据程序框图依次计算得到 ‎ ‎ 结束 故答案为C ‎【点睛】‎ 本题考查了程序框图，意在考查学生对于程序框图的理解能力和计算能力.‎ ‎7．若直线与函数的图象相邻的两个交点之间的距离为1,则函数图象的对称中心为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】先计算周期得到，得到函数表达式，再根据中心对称公式得到答案.‎ ‎【详解】‎ 直线与函数的图象相邻的两个交点之间的距离为1‎ 则 ‎ 的对称中心横坐标为： ‎ 对称中心为 故答案选A ‎【点睛】‎ 本题考查了函数的周期，对称中心，意在考查学生综合应用能力.‎ ‎8．已知样本的平均数是10，方差是2，则的值为（ ）‎ A．88 B．96 C．108 D．110‎ ‎【答案】B ‎【解析】根据平均数和方差公式列方程组，得出和的值，再由 可求得的值。‎ ‎【详解】‎ 由于样本的平均数为，则有，得，‎ 由于样本的方差为，有，得，‎ 即，，因此，，‎ 故选：B。‎ ‎【点睛】‎ 本题考查利用平均数与方差公式求参数，解题的关键在于平均数与方差公式的应用，考查计算能力，属于中等题。‎ ‎9．已知角满足，，且，，则的值为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】根据角度范围先计算和，再通过展开得到答案.‎ ‎【详解】‎ ‎，‎ ‎，‎ 故答案选D ‎【点睛】‎ 本题考查了三角函数恒等变换，将是解题的关键.‎ ‎10．已知函数的值域为，且图像在同一周期内过两点，则的值分别为（ ）‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】先利用可求出的值，再利用、两点横坐标之差的绝对值为周期的一半，计算出周期，再由可计算出 的值，从而可得出答案。‎ ‎【详解】‎ 由题意可知，，‎ ‎、两点横坐标之差的绝对值为周期的一半，则，，‎ 因此，，，故选：C。‎ ‎【点睛】‎ 本题考查三角函数的解析式的求解，求解步骤如下：‎ ‎（1）求、：，；‎ ‎（2）求：根据题中信息求出最小正周期，利用公式求出的值；‎ ‎（3）求：将对称中心点和最高、最低点的坐标代入函数解析式，若选择对称中心点，还要注意函数在该点附近的单调性。‎ ‎11．在中，已知角的对边分别为，若，，，，且，则的最小角的余弦值为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】利用余弦定理求出和的表达式，由，结合正弦定理 得出的表达式，利用余弦定理得出的表达式，可解出的值，‎ 于此确定三边长，再利用大边对大角定理得出为最小角，从而求出。‎ ‎【详解】‎ ‎，由正弦定理，即，‎ ‎，‎ ‎，，‎ 解得，由大边对大角定理可知角是最小角，所以，，故选：D。‎ ‎【点睛】‎ 本题考查正弦定理和余弦定理的应用，考查大边对大角定理，在解题时，要充分结合题中的已知条件选择正弦定理和余弦定理进行求解，考查计算能力，属于中等题。‎ ‎12．若函数有零点，则实数的取值范围为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】令，得，再令，得出，并构造函数，将问题转化为直线与函数 在区间有交点，利用数形结合思想可得出实数的取值范围。‎ ‎【详解】‎ 令，得，‎ ‎，令，‎ 则，所以，，‎ 构造函数，其中，由于，‎ ‎，，‎ 所以，当时，直线与函数在区间有交点，‎ 因此，实数的取值范围是，故选：D。‎ ‎【点睛】‎ 本题考查函数的零点问题，在求解含参函数零点的问题时，若函数中只含有单一参数，可以采用参变量分离法转化为参数直线与定函数图象的交点个数问题，难点在于利用换元法将函数解析式化简，考查数形结合思想，属于中等题。‎ 二、填空题 ‎13．已知扇形的面积为，圆心角为，则该扇形半径为__________．‎ ‎【答案】2‎ ‎【解析】将圆心角化为弧度制，再利用扇形面积得到答案.‎ ‎【详解】‎ 圆心角为 扇形的面积为 故答案为2‎ ‎【点睛】‎ 本题考查了扇形的面积公式，属于简单题.‎ ‎14．有五条线段,长度分别为2,3,5,7,9,从这五条线段中任取三条,则所取三条线段能构成一个三角形的概率为___________．‎ ‎【答案】‎ ‎【解析】列出所有的基本事件，并找出事件“所取三条线段能构成一个三角形”所包含的基本事件，再利用古典概型的概率公式计算出所求事件的概率。‎ ‎【详解】‎ 所有的基本事件有：、、、、、、、、、，共个，‎ 其中，事件“所取三条线段能构成一个三角形”所包含的基本事件有：、、，共个，‎ 由古典概型的概率公式可知，事件“所取三条线段能构成一个三角形”的概率为，‎ 故答案为：。‎ ‎【点睛】‎ 本题考查古典概型的概率的计算，解题的关键就是列举基本事件，常见的列举方法有：枚举法和树状图法，列举时应遵循不重不漏的基本原则，考查计算能力，属于中等题。‎ ‎15．在中，已知角的对边分别为，且，，，若有两解，则的取值范围是__________．‎ ‎【答案】‎ ‎【解析】利用正弦定理得到，再根据有两解得到，计算得到答案.‎ ‎【详解】‎ 由正弦定理得： ‎ 若有两解：‎ 故答案为 ‎【点睛】‎ 本题考查了正弦定理，有两解，意在考查学生的计算能力.‎ ‎16．已知当时，函数（且）取得最小值，则时，的值为__________．‎ ‎【答案】3‎ ‎【解析】先将函数的解析式利用降幂公式化为 ‎，再利用辅助角公式化为，其中 ‎，由题意可知与的关系，结合诱导公式以及求出的值。‎ ‎【详解】‎ ‎ ‎ ‎ ，其中，‎ 当时，函数取得最大值，则，，‎ 所以，，‎ 解得，故答案为：。‎ ‎【点睛】‎ 本题考查三角函数最值，解题时首先应该利用降幂公式、和差角公式进行化简，再利用辅助角公式化简为的形式，本题中用到了与之间的关系，结合诱导公式进行求解，考查计算能力，属于中等题。‎ 三、解答题 ‎17．已知函数，作如下变换：.‎ ‎（1）分别求出函数的对称中心和单调增区间；‎ ‎（2）写出函数的解析式、值域和最小正周期.‎ ‎【答案】（1），；（2），，.‎ ‎【解析】（1）由，直接利用对称中心和增区间公式得到答案.‎ ‎（2）根据变换得到函数的解析式为，再求值域和最小正周期.‎ ‎【详解】‎ 由题意知：（1）‎ 由得对称中心，‎ 由，得：‎ 单调增区间为，‎ ‎（2）所求解析式为：0‎ 值域：‎ 最小正周期：.‎ ‎【点睛】‎ 本题考查了三角函数的对称中心，单调区间，函数变换，周期，值域，综合性强，意在考查学生对于三角函数公式和性质的灵活运用.‎ ‎18．在中，已知角的对边分别为，且.‎ ‎（1）求角的大小；‎ ‎（2）若，，求的面积.‎ ‎【答案】（1）；（2）.‎ ‎【解析】（1）利用边角互化思想得，由结合两角和的正弦公式可求出的值，于此得出角的大小；‎ ‎（2）由余弦定理可计算出，再利用三角形的面积公式可得出的面积。‎ ‎【详解】‎ ‎（1）∵是的内角，‎ ‎∴且，‎ 又由正弦定理：得：‎ ‎，化简得：，‎ 又∵，∴；‎ ‎（2）∵，，‎ ‎∴由余弦定理和（1）得 ，‎ 即，可得：，‎ 又∵，故所求的面积为.‎ ‎【点睛】‎ 本题考查正弦定理边角互化的思想，考查余弦定理以及三角形的面积公式，本题巧妙的地方在于将配凑为，避免利用方程思想求出边的值，考查计算能力，属于中等题。‎ ‎19．为了比较两种治疗失眠症的药(分别称为药, 药)的疗效,随机地选取18位患者服用药,18位患者服用药,这36位患者服用一段时间后,记录他们日平均增加的睡眠时间（单位：）,试验的观测结果如下:‎ 服用药的18位患者日平均增加的睡眠时间：‎ ‎0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3‎ 服用药的18位患者日平均增加的睡眠时间：‎ ‎3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7‎ ‎（1）分别计算两组数据的平均数(小数点后保留两位小数),从计算结果看哪种药疗效更好?‎ ‎（2）根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?并说明理由.‎ ‎【答案】（1），，服用 种药的疗效更好；（2）详见解析.‎ ‎【解析】（1）分别计算出服用药的位患者和药的位患者日平均增加的睡眠时间的平均数，比较两平均数的大小，选择平均数较大的作为疗效较好的；‎ ‎（2）补充茎叶图，根据茎叶图的数据分布情况来比较两种药的疗效。‎ ‎【详解】‎ ‎（1）服用药的18位患者日平均增加的睡眠时间的平均数为 服用药的18位患者日平均增加的睡眠时间的平均数为 ‎∵，∴服用种药的疗效更好；‎ ‎（2）由观测结果可绘制如下茎叶图：‎ 药（叶）‎ 茎 药（叶）‎ ‎6 ‎ ‎0‎ ‎5 6 8 9‎ ‎8 5 5 2 2 ‎ ‎1‎ ‎1 2 2 3 6 7 8 9‎ ‎9 8 7 7 6 5 3 3 2 ‎ ‎2‎ ‎1 4 5 6 7‎ ‎2 1 0 ‎ ‎3‎ ‎2‎ 从以上茎叶图可以看出，药疗效的试验结果有的叶集中在茎2,3上，而药疗效的试验结果有的叶集中在茎0,1上，由此可看出药的疗效更好。‎ ‎【点睛】‎ 本题考查平均数的计算，考查利用茎叶图数据的分布来估计总体，一般来讲，平均数大小的比较要看数集中在哪些茎附近，而样本的稳定性程度则取决于数据的集中性程度，一般来讲，茎叶图越矮胖，样本的稳定性越差，茎叶图越瘦高，样本的稳定性越好。‎ ‎20．已知向量，，.‎ ‎（1）若，求的值；‎ ‎（2）设，若恒成立，求的取值范围.‎ ‎【答案】（1）；（2）.‎ ‎【解析】（1）由，转化为，利用弦化切的思想得出的值，从而求出的值；‎ ‎（2）由，转化为，然后利用平面向量数量积的坐标运算律和辅助角公式与函数的解析式进行化简，并求出在区间的最大值，即可得出实数的取值范围。‎ ‎【详解】‎ ‎（1）∵，且，，，‎ ‎∴，即，又∵，∴；‎ ‎（2）易知，，‎ ‎∵，∴，，‎ 当时，，取得最大值：，‎ 又恒成立，即，故。‎ ‎【点睛】‎ 本题考查平面向量数量积的坐标运算，考查三角函数的最值，在求解含参函数的不等式恒成立问题，可以利用参变量分离法，转化为函数的最值来求解，考查转化与化归数学思想，考查计算能力，属于中等题。‎ ‎21．驻马店市政府委托市电视台进行“创建森林城市”知识问答活动,市电视台随机对该市15～65岁的人群抽取了人,绘制出如图1所示的频率分布直方图,回答问题的统计结果如表2所示.‎ ‎（1）分别求出的值；‎ ‎（2）从第二、三、四、五组回答正确的人中用分层抽样的方法抽取7人,则从第二、三、四、五组每组回答正确的人中应各抽取多少人?‎ ‎（3）在(2)的条件下,电视台决定在所抽取的7人中随机选2人颁发幸运奖,求所抽取的人中第二组至少有1人获得幸运奖的概率.‎ ‎【答案】（1），，，；（2）2人,3人,1人,1人；（3）.‎ ‎【解析】（1）先计算出总人数为1000人，再根据公式依次计算的值.‎ ‎（2）根据分层抽样规律得到从第二、三、四、五组每组回答正确的人中应分别抽取:2人,3人,1人,1人 ‎（3）排出所有可能和满足条件的情况，得到概率.‎ ‎【详解】‎ ‎（1）依题和图表：‎ 由得：，‎ 由得：，‎ 由得：，‎ 由得：，‎ 由得：，‎ 故所求，，，.‎ ‎（2）由以上知:第二、三、四、五组回答正确的人数分别为:180人,270人,90人,90人 用分层抽样抽取7人,则:‎ 从第二组回答正确的人中应该抽取: 人，‎ 从第三组回答正确的人中应该抽取：人，‎ 从第四组回答正确的人中应该抽取: 人，‎ 从第五组回答正确的人中应该抽取: 人，‎ 故从第二、三、四、五组每组回答正确的人中应分别抽取:2人,3人,1人,1人；‎ ‎（3）设从第二组回答正确的人抽取的2人为: ，‎ 从第三组回答正确的人抽取的3人为: ‎ 从第四组回答正确的人抽取的1人为: ‎ 从第五组回答正确的人抽取的1人为: ‎ 随机抽取2人,所有可能的结果有: ，，，，，，，，，，，，，，，，，，，，，共21个基本事件，其中第二组至少有1人被抽中的有：，，，，，，，，，，共这11个基本事件.‎ 故抽取的人中第二组至少有1人获得幸运奖的概率为：.‎ ‎【点睛】‎ 本题考查了频率直方图，分层抽样，概率的计算，意在考查学生的应用能力和计算能力.‎ ‎22．已知函数.‎ ‎（1）求函数的最小正周期和值域；‎ ‎（2）设为的三个内角，若，，求的值.‎ ‎【答案】（1）周期，值域为；（2）.‎ ‎【解析】（1）利用二倍角降幂公式与辅助角公式将函数的解析式进行化简，利用周期公式求出函数的最小正周期，并求出函数的值域；‎ ‎（2）先由的值，求出角的值，然后由结合同角三角函数的基本关系以及两角和的余弦公式求出的值。‎ ‎【详解】‎ ‎（1）∵且，‎ ‎∴故所求周期，值域为；‎ ‎（2）∵是的三个内角，，∴‎ ‎∴又，即，‎ 又∵，‎ 故 ，‎ 故.‎ ‎【点睛】‎ 本题考查三角函数与解三角形的综合问题，考查三角函数的基本性质以及三角形中的求值问题，求解三角函数的问题时，要将三角函数解析式进行化简，结合正余弦函数的基本性质求解，考查分析问题的能力和计算能力，属于中等题。‎