2018-2019学年安徽省合肥九中高二上学期期中考试数学试题（Word版） 6页

合肥九中2018-2019学年第一学期期中考试 高二数学试卷 考试范围：必修二（不含空间直角坐标系）；考试时间：120分钟；满分：150分；命题人：杨新宁 审题：杨向前 注意：本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题，所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题，所有答案必须填在答题卷的相应位置。答案写在试卷上均无效，不予记分。‎ 第I卷 一、选择题（本大题共12小题，每小题5分，共60.0分）‎ 1. 直线的倾斜角为　 　‎ A. B. C. D. ‎ 2. 设m，n是两条不同的直线，，是两个不同的平面，则下列命题正确的是　 　‎ A. 若，，则 B. 若，，则 ‎ C. 若，，，则 D. 若，，，则 3. 已知直线：和：互相平行，则实数　 　‎ A. B. C. 或3 D. 或 4. 已知直线；，：，若，则a的值为　 　‎ A. 8 B. 2 C. D. ‎ 5. 在正方体中，E为棱CD的中点，则　 　‎ A. B. C. D. ‎ 6. 圆的圆心到直线的距离为1，则　 　‎ A. B. C. D. 2‎ 7. 体积为8的正方体的顶点都在同一球面上，则该球面的表面积为　 　‎ A. B. C. D. ‎ 8. 直线l过点，被圆C：截得的弦长为，则直线l的方程是　 　‎ A. B. C. D. 或 9. 已知圆的方程为，过点的该圆的所有弦中，最短弦的长为　 　‎ A. B. 1 C. 2 D. 4‎ 10. 已知一个几何体的三视图如图所示，则该几何体的体积为　 　‎ A. B. C. ‎ ‎ D. 12 ‎ 1. 已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为　 　‎ A. B. C. D. ‎ 2. 直线与曲线有两个不同的交点，则实数的k的取值范围是　 　‎ A. B. C. D. ‎ 第II卷 二、填空题（本大题共4小题，每小题5分，共20.0分）‎ 3. 直线l：与圆相交于M，N两点，则线段MN的长为 ．‎ 4. 垂直于x轴的直线l被圆截得的弦长为，则l的方程为 ．‎ 5. 给出下面四个命题，其中a，b，c都是直线：‎ ‎    若a，b异面，b，c异面，则a，c异面；  若a，b相交，b，c相交，则a，c相交；‎ ‎    若，则a，b与c所成的角相等；  若，，则．‎ ‎    其中真命题的个数是 ．‎ 6. 已知A，B是球O的球面上两点，，C为该球面上的动点若三棱锥体积的最大值为3，则球O的体积为 ．‎ 三、解答题（本大题共6小题，共70.0分）‎ 7. 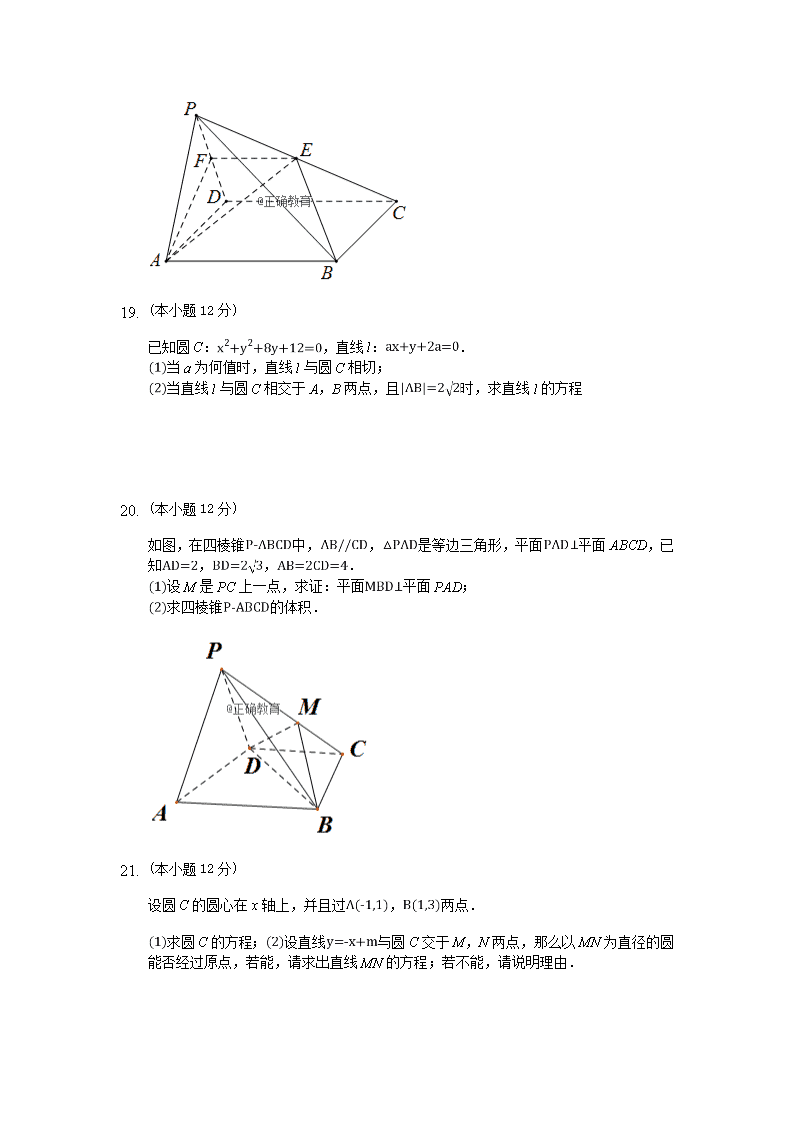‎(本小题10分) ‎ ‎ 已知圆C的圆心在直线，半径为5，且圆C经过点和点求圆C的标准方程； ‎ 8. ‎(本小题12分) ‎ 如图，在四棱锥中，底面ABCD是正方形点E是棱PC的中点，平面ABE与棱PD交于点F． 求证：； 若，且平面平面ABCD，求证：平面PCD．‎ 1. ‎(本小题12分) ‎ 已知圆C：，直线l：． 当a为何值时，直线l与圆C相切； 当直线l与圆C相交于A，B两点，且时，求直线l的方程 ‎ 2. ‎(本小题12分) ‎ 如图，在四棱锥中，，是等边三角形，平面平面ABCD，已知，，． 设M是PC上一点，求证：平面平面PAD； 求四棱锥的体积．‎ 3. ‎(本小题12分) ‎ 设圆C的圆心在x轴上，并且过，两点．‎ 求圆C的方程；设直线与圆C交于M，N两点，那么以MN为直径的圆能否经过原点，若能，请求出直线MN的方程；若不能，请说明理由． ‎ 1. ‎(本小题12分) ‎ ‎ 如图，三棱柱中，侧面为菱形，的中点为O，且平面C. 证明：； 若，，，求三棱柱的高． ‎ 合肥九中2018-2019学年第一学期期中考试 高二数学试卷答案 ‎【答案】‎ ‎1. D 2. B 3. C 4. D 5. C 6. B 7. A 8. D 9. C 10. A 11. B 12. A ‎ ‎13.    14. ，或   15. 1   16.   ‎ ‎17. 解：设圆C：， 点C在直线上，则有，圆C经过点和点， 即：，解得：，． 所以，圆C：  ‎ ‎18. 解：证明：底面ABCD是正方形，，又平面PCD，平面PCD， 平面PCD，又，B，E，F四点共面，且平面平面， 证明：在正方形ABCD中，，又平面平面ABCD，且平面平面，平面ABCD，平面PAD 平面PAD，又平面PAD， ， 由可知，，又，C，D，E，F 在同一平面内， ，点E是棱PC中点，点F是棱PD中点，在中，， ，又，PD、平面PCD，平面PCD．  ‎ ‎19. 解：将圆C的方程 配方得标准方程为，则此圆的圆心为，半径为2．若直线l与圆C相切，则有，；        过圆心C作，则根据题意和圆的性质， ，或7． 故所求直线方程为或．  ‎ ‎20. 证明：在三角形ABD中由勾股定理得， 又平面平面ABCD，平面平面， 所以平面PAD，又平面BDM，所以平面平面PAD； 解：取AD中点为O，则PO是四棱锥的高， 底面ABCD的面积是三角形ABD面积的，即， 所以四棱锥的体积为．  ‎ ‎21. 解：Ⅰ根据题意，设圆心坐标为，半径为r， 则其标准方程为：， 由于点和在圆C上，则有， ， 联立，解可得，‎ ‎， 故圆的标准方程为：； Ⅱ设，是直线与圆C的交点， 联立与可得：， 则有，，则MN中点H的坐标为， 假设以MN为直径的圆经过原点，则有，圆心C到MN的距离， 则有，又由，则有，解可得，经检验，时，直线与圆相交，符合题意； 故直线MN的方程为：或．  ‎ ‎22. 证明：连接，则O为与的交点，侧面为菱形， ，平面，， ，平面ABO，平面ABO， ； 解：作，垂足为D，连接AD，作，垂足为H， ，，，平面AOD， ，，，平面ABC， ，为等边三角形，，， ，，由，可得，，为的中点，到平面ABC的距离为，三棱柱的高．  ‎