- 9.51 MB
- 2021-06-02 发布
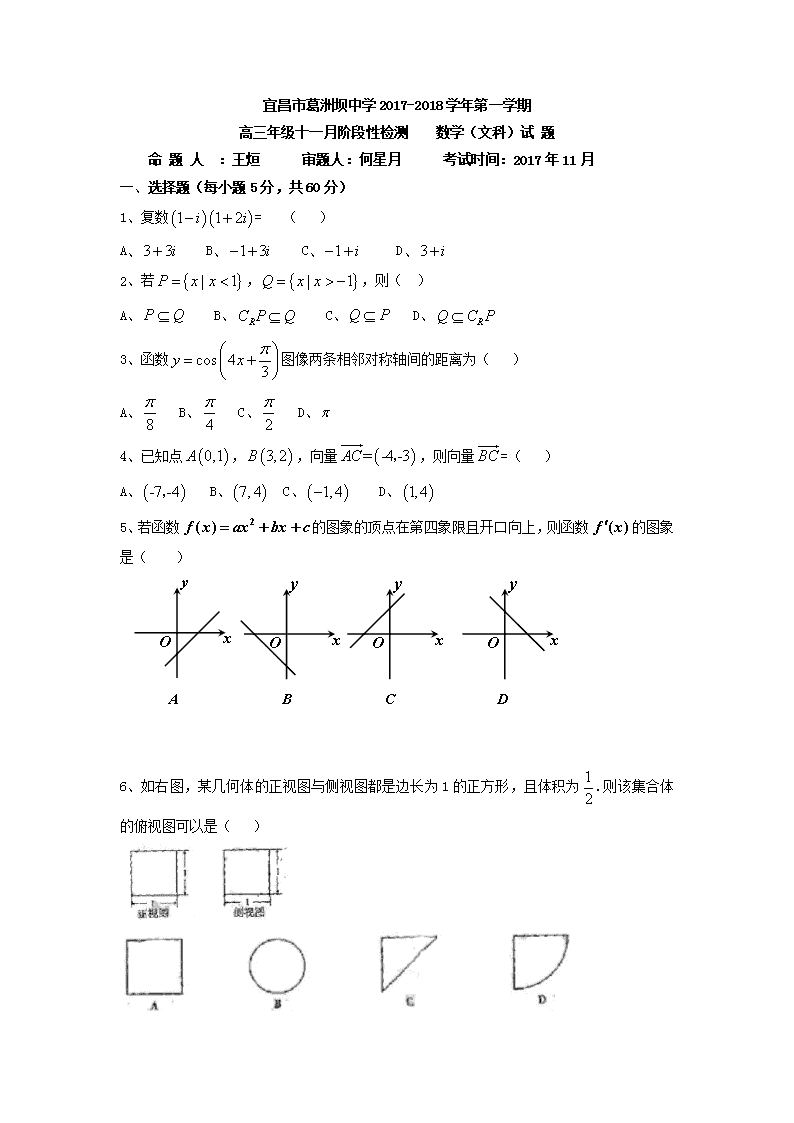
宜昌市葛洲坝中学2017-2018学年第一学期
高三年级十一月阶段性检测 数学(文科)试 题
命 题 人 :王烜 审题人:何星月 考试时间:2017年11月
一、选择题(每小题5分,共60分)
1、复数= ( )
A、 B、 C、 D、
2、若,,则( )
A、 B、 C、 D、
3、函数图像两条相邻对称轴间的距离为( )
A、 B、 C、 D、
4、已知点,,向量,则向量=( )
A、 B、 C、 D、
5、若函数的图象的顶点在第四象限且开口向上,则函数的图象是( )
6、如右图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为.则该集合体的俯视图可以是( )
7、若直线与圆相交于A,B两点,则的值为( )
A、-1 B、0 C、1 D、6
8、设双曲线的半焦距为,直线过两点,已知原点到直线的距离为,则双曲线的离心率为( )
A、2 B、 C、 D、
9、满足约束条件,若取得最大值的最优解不唯一,则实数的值为( )
A、或 B、2或 C、2或1 D、2或-1
10、已知椭圆:与圆,若在椭圆上存在点,使得由点所作的圆的两条切线互相垂直,则椭圆的离心率的取值范围是( )
A、 B、 C、 D、
11、在直三棱柱中,平面与棱分别交于点,且直线.有下列三个命题:①四边形是平行四边形;②平面平面;③平面平面.其中正确的命题有( )
A、①② B、②③ C、①③ D、①②③
12、已知函数,且,则的最小值为( )
A、 B、 C、 D、
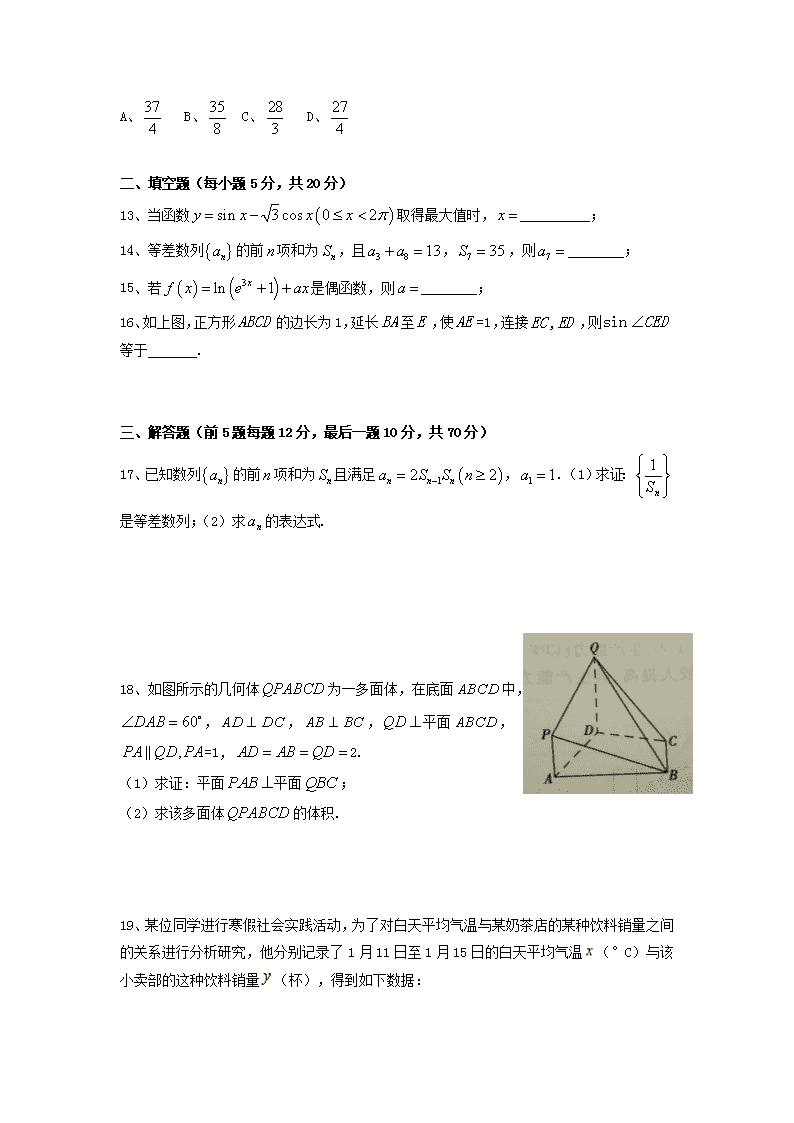
二、填空题(每小题5分,共20分)
13、当函数取得最大值时, ;
14、等差数列的前项和为,且,,则 ;
15、若是偶函数,则 ;
16、如上图,正方形的边长为1,延长至,使=1,连接,则等于 .
三、解答题(前5题每题12分,最后一题10分,共70分)
17、已知数列的前项和为且满足,.(1)求证:是等差数列;(2)求的表达式.
18、如图所示的几何体为一多面体,在底面中,
,,,平面,
=1,2.
(1)求证:平面平面;
(2)求该多面体的体积.
19、某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温(°C)与该小卖部的这种饮料销量(杯),得到如下数据:
日期
1月11日
1月12日
1月13日
1月14日
1月15日
平均气温(°C)
9
10
12
11
8
销量(杯)
23
25
30
26
21
(Ⅰ)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(Ⅱ)请根据所给五组数据,求出y关于x的线性回归方程;
(Ⅲ)根据(Ⅱ)中所得的线性回归方程,若天气预报1月16日的白天平均气温7(°C),请预测该奶茶店这种饮料的销量.
(参考公式:.)(其中)
20、设函数.(1)求的单调区间和极值;(2)证明:若存在零点,则在区间上仅有一个零点.
21、已知抛物线的焦点也是椭圆的一个焦点,与的公共弦的长为.过点的直线与相交于两点,与相交于两点,且与同向.
(1)求的方程;(2)若,求直线的斜率.
22、在平面直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立坐标系,曲线的极坐标方程为,直线的参数方程为(为参数),与交于两点.
(1)求曲线的直角坐标方程及的普通方程;
(2)求的值.
答案
一、选择题
DBBAA CBADC CA
二、填空题
13、; 14、8; 15、; 16、
三、解答题
17、(1)略(2)
18、(1)略(2)
19、(Ⅰ)设“选取的2组数据恰好是相邻2天数据”为事件A,
所有基本事件(m,n)(其中m,n为1月份的日期数)有:(11,12),(11,13),(11,14),
(11,15),(12,13),(12,14),(12,15),(13,14),(13,15),(14,15),共有10种.
事件A包括的基本事件有(11,12),(12,13),(13,14),(14,15)共4种.
所以为所求
(Ⅱ)由数据,求得,.
由公式,求得,,
所以y关于x的线性回归方程为
(Ⅲ)当x=7时,.所以该奶茶店这种饮料的销量大约为19杯
20、(1)的单调递减区间是,单调递增区间是;
在取得最小值.
(2)略
21、(1); (2)
22、(1);(2)