安徽省合肥市第二中学2019届高三下学期藏高三第二次模拟联考数学（文）试题答案 5页

数学（文科）答案 一．选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的。‎ ‎1-5 CDCBA 6-10 ADBDA 11-12 DC 二．填空题：本大题共4小题，每小题5分。‎ ‎13. -8 14. 15. 2 16. 45‎ 三．解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤。‎ ‎17. 解：（1） 由已知及正弦定理得：，‎ ‎∵，∴，‎ ‎∵∴，∵∴．‎ ‎（2）∵，的周长8，∴，‎ 由余弦定理得，∴，‎ 的面积 ‎18.解：（1）第1组的频数为人，所以①处应填的数为，‎ 从而第2组的频数为，因此②处应填的数为．‎ 频率分布直方图如图所示，‎ ‎（2）设第3组的2名选手为，第4组的2名选手为，第5组的1名选手为，则从这5名选手中抽取2名选手的所有情况为，，，共10种，其中第4组的2名选手中至少有1名选手人选的有，共7种，所以第4组至少有1名选手被考官面试的概率为．‎ ‎19.解：(1)由PA⊥底面ABCD得，PA⊥AE.‎ 由底面ABCD为菱形，∠ABC＝60°，得△ABC为等边三角形，又E为BC的中点，得AE⊥BC，所以AE⊥AD.因为PA∩AD＝A，所以AE⊥平面PAD.(6分)‎ ‎(2)令多面体PAECF的体积为V，则V＝VPAEC＋VCPAF.‎ VPAEC＝××PA＝××2＝；VCPAF＝××AE＝××＝.‎ 故多面体PAECF的体积V＝＋＝.(12分)‎ ‎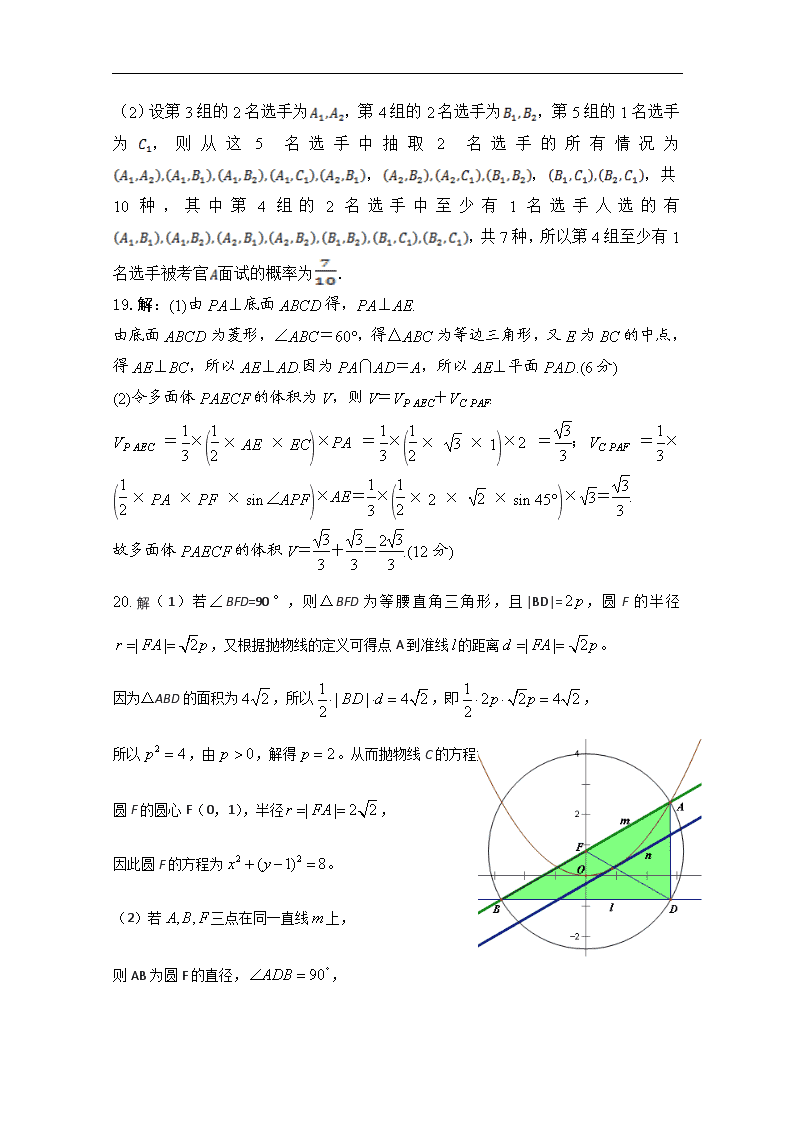20.解（1）若∠BFD=90°，则△BFD为等腰直角三角形，且|BD|=，圆F的半径，又根据抛物线的定义可得点A到准线的距离。‎ 因为△ABD的面积为，所以，即，‎ 所以，由，解得。从而抛物线C的方程为，‎ 圆F的圆心F（0，1），半径，‎ 因此圆F的方程为。‎ （2） 若三点在同一直线上，‎ 则AB为圆F的直径，，‎ 根据抛物线的定义，得，‎ 所以，从而直线的斜率为或。‎ 当直线的斜率为时，直线的方程为，原点O到直线的距离。依题意设直线的方程为，联立，得，因为直线与C只有一个公共点，所以，从而。所以直线的方程为，原点O到直线的距离。因此坐标原点到，距离的比值为。‎ 当直线的斜率为时，由图形的对称性可知，坐标原点到，距离的比值也为3。‎ ‎21.解：(1)h(x)的定义域为(0，＋∞)，‎ h′(x)＝－＋－2＝－＝－，‎ 令h′(x)<0，得h(x)的单调递减区间是和(1，＋∞)．‎ ‎(2)问题等价于aln x＝有唯一的实根．‎ 显然a≠0，则关于x的方程xln x＝有唯一的实根．‎ 构造函数φ(x)＝xln x，则φ′(x)＝1＋ln x.‎ 令φ′(x)＝1＋ln x＝0，得x＝e－1.‎ 当0e－1时，φ′(x)>0，φ (x)单调递增．‎ 所以φ(x)的极小值为φ(e－1)＝－e－1.‎ 如图，作出函数φ(x)的大致图象，则要使方程xln x＝有唯一的实根，只需直线y＝与曲线y＝φ(x)有唯一的交点，则＝－e－1或>0，解得a＝－e或a>0.‎ 故实数a的取值范围是{－e}∪(0，＋∞)．‎ 22. 解（1）曲线，即，即，即或，‎ 由于曲线过极点，∴曲线的极坐标方程为，直线，即，‎ 即，即，‎ 直线的极坐标方程为；‎ ‎（2）由题得，设为线段的中点，圆心到直线的距离为，‎ 则它在时是减函数，‎ ‎∴的取值范围．‎ 23. 解：（1）当时，不等式可化为：‎ 则或或 解得或，所以不等式 的解集为 。‎ （2） 等价于，而，且当时等号成立，故等价于，可得，所以的取值范围是