广东省汕头市潮南区东山中学2013届高三上学期第四次月考数学（理）试题 11页

潮南区东山中学高三第四次月考试卷 数学（理科）‎ 参考公式： 　　　　　　　　‎ 一、 选择题：（本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项 ‎ 符合题目要求.）‎ ‎1. 已知复数 (为虚数单位），则复数在复平面上所对应的点位于 （ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2．集合，若，则实数的值为（ ）‎ A．或 B． C．或 D． ‎ ‎3. 等差数列的前项和为，且，，则公差等于（ ）‎ A．1 B. C. D. ‎ ‎4. 已知向量，且，则等于（ ）‎ A． B． C． 　　 D． ‎ ‎5. “”是“”的（ ）‎ A．充分不必要条件 B．既不充分也不必要条件 C．充要条件 D. 必要不充分条件 ‎ ‎6．从6人中选4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览，要求每个城市有一人游览，每人只游览一个城市，且这6人中甲、乙两人不去巴黎游览，则不同的选择方案共有（ ）‎ ‎ A．300种 B．240种 C．144种 D．96种 ‎7． 已知函数，给出下面四个命题：①函数的最小正周期为；‎ ‎②函数是偶函数；③函数的图象关于直线对称；④函数在区间上是增函数，其中正确命题的个数是 A．1个 B．2个 C．3个 D．4个 ‎8．已知函数，若有，则的取值范围为（ ）‎ A． B． C． D．‎ 二．填空题（本大题共7小题，分为必做题和选做题两部分。每小题5分，满分30分）‎ ‎（一）必做题：第9至13题为必做题，每道试题考生都必须作答．‎ ‎9．函数的定义域为 ．‎ ‎10. 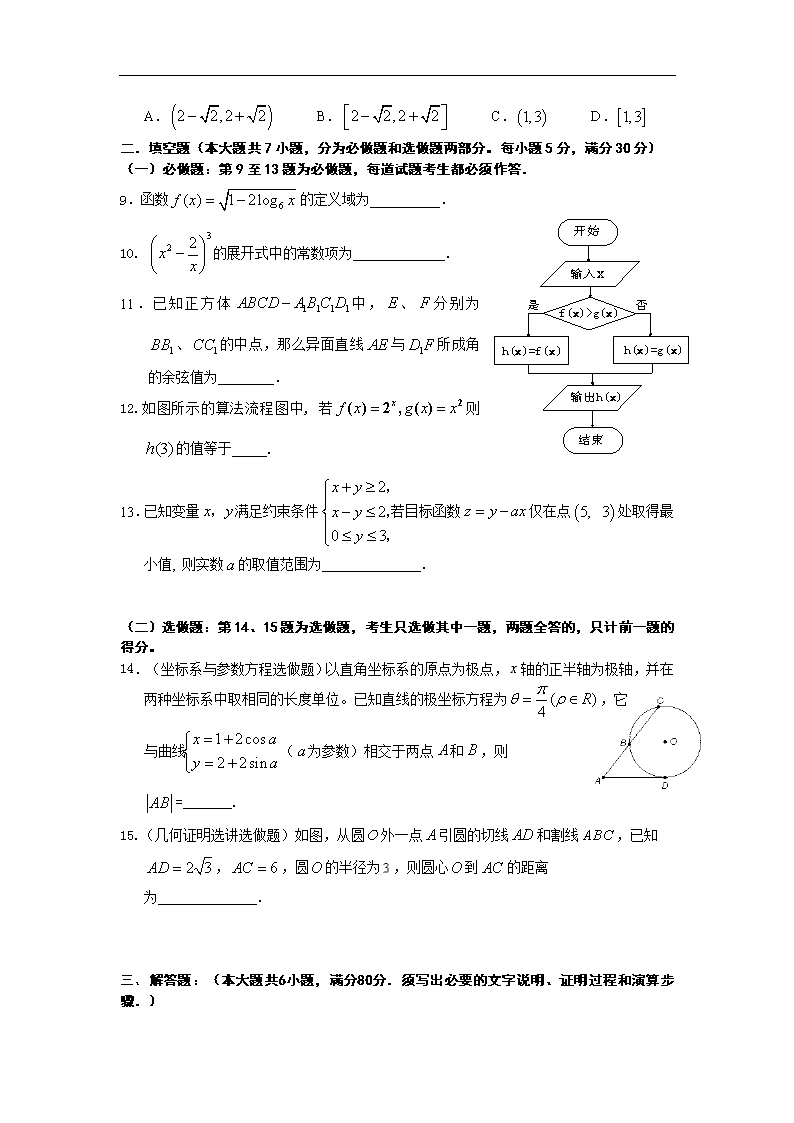的展开式中的常数项为 ．‎ ‎11．已知正方体中，、分别为、的中点，那么异面直线与所成角的余弦值为________．‎ ‎12.如图所示的算法流程图中, 若则的值等于 .‎ ‎13．已知变量满足约束条件若目标函数仅在点处取得最小值, 则实数的取值范围为 ．‎ ‎（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的，只计前一题的得分。‎ ‎14．（坐标系与参数方程选做题）以直角坐标系的原点为极点，轴的正半轴为极轴，并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为，它与曲线（为参数）相交于两点和，则=_______.‎ ‎15.（几何证明选讲选做题）如图，从圆外一点引圆的切线和割线，已知，，圆的半径为，则圆心到的距离为　　　　　　　．‎ 三、解答题：（本大题共6小题，满分80分．须写出必要的文字说明、证明过程和演算步骤．）‎ ‎16．（本小题满分12分）‎ 已知向量,,且，为锐角. ‎ ‎（1）求角的大小； ‎ ‎（2）求函数的值域.‎ ‎17．（本小题满分12分）‎ 已知等比数列{an}的公比q=3，前3项和S3=。‎ ‎（1）求数列{an}的通项公式；‎ ‎ （2）若函数在处取得最大值，且最大值 ‎ 为 a3，求函数f（x）的解析式。‎ ‎18．（本题满分14分）‎ 某商场准备在节日期间举行促销活动，根据市场调查，该商场决定从3种服装商品、2种家电商品、4种日用商品中，选出3种商品进行促销活动。‎ ‎ （1）试求选出的3种商品中至少有一种日用商品的概率；‎ ‎ （2）商场对选出的商品采用有奖促销，即在该商品现价的基础上价格提高180元，同时允许顾客每购买1件促销商品有3次抽奖的机会，若中奖，则每次中奖都可获得奖金100元，假设顾客每次抽奖时中奖与否是等可能的，试分析此种有奖促销方案对商场是否有利。‎ ‎19.（本小题满分14分）‎ ‎ 如图，在三棱柱中，侧棱底面,，为的中点, .‎ ‎ (1) 求证：平面；‎ ‎ (2) 若四棱锥的体积为, ‎ 求二面角的正切值.‎ ‎ 20．（本小题满分14分）‎ 设为数列的前项和，对任意的，都有(为正常数)．‎ ‎（1）求证：数列是等比数列；‎ ‎（2）数列满足，求数列的通项公式；‎ ‎（3）在满足（2）的条件下，求数列的前项和．‎ ‎ 21．（本小题满分14分）‎ 已知函数是奇函数，且图像在点 处的切线斜率为3‎ ‎（为自然对数的底数）．‎ ‎（1）求实数、的值；‎ ‎（2）若，且对任意恒成立，求的最大值；‎ ‎（3）当时，证明：．‎ 数学（理科）参考答案与评分标准 一．选择题：共8小题，每小题5分，满分40分 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 B ‎ C ‎1．【解析】1.提示:因为,所以对应的点在复平面的第二象限. 故选．‎ ‎2．【解析】由可知或,故选．‎ ‎3．【解析】且，，.故选 ‎4．【解析】由，得，即，所以，‎ 故选[‎ ‎5．【解析】注意的正负号.故选．‎ ‎8.【解析】由题可知，，若有，则，即，解得。故选．‎ 二．填空题：共7小题，每小题5分，满分30分．其中14~15题是选做题，考生只选做一题．‎ ‎9． 10． 11． 12． 13． ‎ ‎14． 15． ‎ ‎9．【解析】根据二次根式和对数函数有意义的条件，得 。 ‎ ‎10．【解析】的展开式中的常数项即。‎ ‎11．【解析】连接，则,所以与所成的角即为异面直线所成的角，设边长为，则，在三角形中.‎ ‎12．【解析】，由数形结合可知，当时, 所以有 ‎13．【解析】目标函数可变为直线，斜率为，仅在点处取得 最小值,只须 ‎14．【解析】直线的普通方程为，曲线的普通方程 ‎15．【解析】先用切割线定理求出的长度,然后距离 三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤.‎ ‎16．（本小题满分分）‎ 解：（1）由题意得………2分 ‎ ， ………4分 由为锐角 ， 得, ………6分 ‎（2）由（1）可得 ………7分 所以 ………9分 因为，则，‎ 当时，有最大值. 当时，有最小值， ………11分 故所求函数的值域是. ………12分 ‎17．（本小题满分12分）‎ 解：I）由 解得　所以 ‎（II）由（I）可知 因为函数的最大值为3，所以A=3。‎ 因为当时取得最大值，所以 又　所以函数的解析式为 ‎18．（本小题满分14分）‎ 解：（1）从3种服装商品、2种家电商品、4种日用商品中，选出3种商品，一共有 种不同的选法，选出的3种商品中，没有日用商品的选法有种，……2分 所以选出的3种商品中至少有一种日用商品的概率为 ……4分 ‎（2）顾客在三次抽奖中所获得的奖金总额是一随机变量，其所有可能的取值为0，100，200，300。（单元：元） ……6分 表示顾客在三次抽奖中都没有获奖，所以，……7分 同理可得 ,‎ ‎ ……9分 于是顾客在三次抽奖中所获得的奖金总额的期望值是 ‎ …………11分 故促销方案对商场有利。 …………12分 ‎19．（本小题满分14分）‎ ‎（1）证明: 连接,设与相交于点,连接,‎ ‎ ∵ 四边形是平行四边形,∴点为的中点. ‎ ‎∵为的中点，∴为的中位线,‎ ‎∴ . …… 2分 ‎∵,‎ ‎∴. …… 4分 ‎(2)解: 依题意知，，‎ ‎ ∵, ‎ ‎∴ ‎ 作，垂足为，则， ……6分 设，‎ 在中，，，‎ ‎∴四棱锥的体积 ‎ 。 …… 8分 依题意得，，即. …… 9分 ‎(以下求二面角的正切值提供两种解法)‎ 解法1:∵,‎ ‎，，∴.…… 10分 取的中点，连接，则,且.‎ ‎∴.‎ 作，垂足为，连接，由于，且，‎ ‎∴. 又∵,∴.‎ ‎∴. …… 12分 由,得,得,‎ 在中, .‎ ‎∴二面角的正切值为. …… 14分 解法2: ∵,， 平面，‎ ‎ ∴. …… 10分 以点为坐标原点,分别以所在直线为轴,‎ ‎ 轴和轴,建立空间直角坐标系. ‎ ‎ 则,,,.‎ ‎ ∴,‎ ‎ 设平面的法向量为, ‎ ‎ 由及,得 ‎ 令,得.‎ ‎ 故平面的一个法向量为, …… 11分 ‎ 又平面的一个法向量为,‎ ‎ ∴. …… 12分 ‎ ∴. …… 13分 ‎ ∴.‎ ‎ ∴二面角的正切值为. …… 14分 ‎20．（本小题满分14分）‎ ‎（1）证明：当时，，解得．…………………1分 当时，．即．…………………2分 又为常数，且，∴．………………………3分 ‎∴数列是首项为1，公比为的等比数列．……………………4分 ‎（2）解：． ………………………5分 ‎∵，∴，即．………………7分 ‎∴是首项为，公差为1的等差数列．………………………………………8分 ‎∴，即．……………………………9分 ‎（3）解：由（2）知，则．‎ 所以， …10分 即， ① ……11分 则， ②………12分 ‎②－①得，……………………13分 故．……………………14分 ‎21．（本小题满分14分）‎ 解：（1）是奇函数，所以，即 ‎ ……1分，‎ 所以，从而 ……2分，‎ 此时， ……3分，‎ 依题意，所以 ……4分 ‎（2）当时，设，‎ 则 ……5分 设，则，在上是增函数 因为，，‎ 所以，使 ……7分 时，，，即在上为减函数；‎ 同理在上为增函数 从而的最小值为 所以，的最大值为 ……9分。‎ ‎（3）要证，即要证……10分，‎ 即证， ……11分，‎ 设， ……12分，‎ 则 设，则，在上为增函数，‎ ‎，，‎ 从而，在上为增函数 因为，所以，，‎ 所以 ……14分