数学（理）卷·2018届重庆市大学城一中高二上学期期中考试（2016-11） 8页

‎2016-2017学年度大学城一中高2018级期中考试 数 学 试 题 一、选择题（每小题5分，共60分）‎ ‎1．直线不经过的象限是( )‎ A．第四象限 B．第三象限 C．第二象限 D．第一象限 ‎2．已知直线l经过点A（﹣2，0）与点B（﹣5，3），则该直线的倾斜角为（　　）‎ A．150° B．135° C．60° D．45°‎ ‎3．关于直线m，n与平面α，β，有以下四个命题：‎ ‎①若m∥α，n∥β且α∥β，则m∥n；‎ ‎②若m⊥α，n⊥β且α⊥β，则m⊥n；‎ ‎③若m⊥α，n∥β且α∥β，则m⊥n；‎ ‎④若m∥α，n⊥β且α⊥β，则m∥n；‎ 其中真命题的序号是（　　）‎ A．①② B．③④ C．①④ D．②③‎ ‎4．直线被圆所截得的弦长为(  )‎ A. B‎.1 ‎ C. D.‎ ‎5．已知在四面体ABCD中，E，F分别是AC，BD的中点，若AB=2，CD=4，EF⊥AB，则EF与CD所成的角的度数为（　　）‎ A．90° B．45° C．60° D．30°‎ ‎6．已知直线l过点P（，1），圆C：x2+y2=4，则直线l与圆C的位置关系是（　　）【来源：全,品…中&高*考+网】‎ A．相交 B．相切 C．相交和相切 D．相离 ‎7．已知底面边长为1，侧棱长为的正四棱柱的各顶点均在同一个球面上，则该球的表面积为（ ）‎ A. B C. D. ‎ ‎8．如图，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为（ ）‎ A. B.4 ‎ C. D.2‎ ‎ ‎ ‎9．方程（x﹣）=0表示的曲线为（　　）‎ A．一条线段与半圆 B．一条射线与一段劣弧 C．一条射线与一个圆 D．一条直线和一个圆 ‎10．已知四棱锥S－ABCD的所有棱长都相等，E是SB的中点，则AE，SD所成的角的正弦值为(  )‎ A． B． C． D．‎ ‎11．直线ax＋by＋c＝0与圆x2＋y2＝9相交于两点M、N，若c2＝a2＋b2，则·(O为坐标原点)等于(　)‎ A．－7 B．－‎14 C．7 D．14‎ ‎12.如果直线和函数的图象恒过同一个定点，且该定点始终落在圆的内部或圆上，那么的取值范围是（ ）【来源：全,品…中&高*考+网】‎ A． B． C． D．‎ 第II卷（非选择题）‎ 二、填空题（每小题5分，共20分）‎ ‎13．圆x2+y2+4x﹣4y﹣1=0与圆x2+y2+2x﹣13=0相交于P，Q两点，则直线PQ的方程为　　．‎ ‎14．已知直线l经过点（1，3），且与圆x2+y2=1相切，直线l的方程为　　．‎ ‎15. 一个水平放置的边长为4的等边△ABC，运用斜二测画法得到直观图为△A′B′C′，则△A′B′C′的面积为　　．‎ ‎16．在三棱锥P-ABC中侧棱PA，PB，PC两两垂直，Q为底面△ABC内一点，若点Q到三个侧面的距离分别为3,4,5，则过点P和Q的所有球中，表面积最小的球的表面积为 .‎ 三、解答题（70分）‎ ‎17．（10分）已知直线和的相交于点P。‎ 求：（Ⅰ）过点P且平行于直线的直线方程；‎ ‎（Ⅱ）过点P且垂直于直线的直线方程。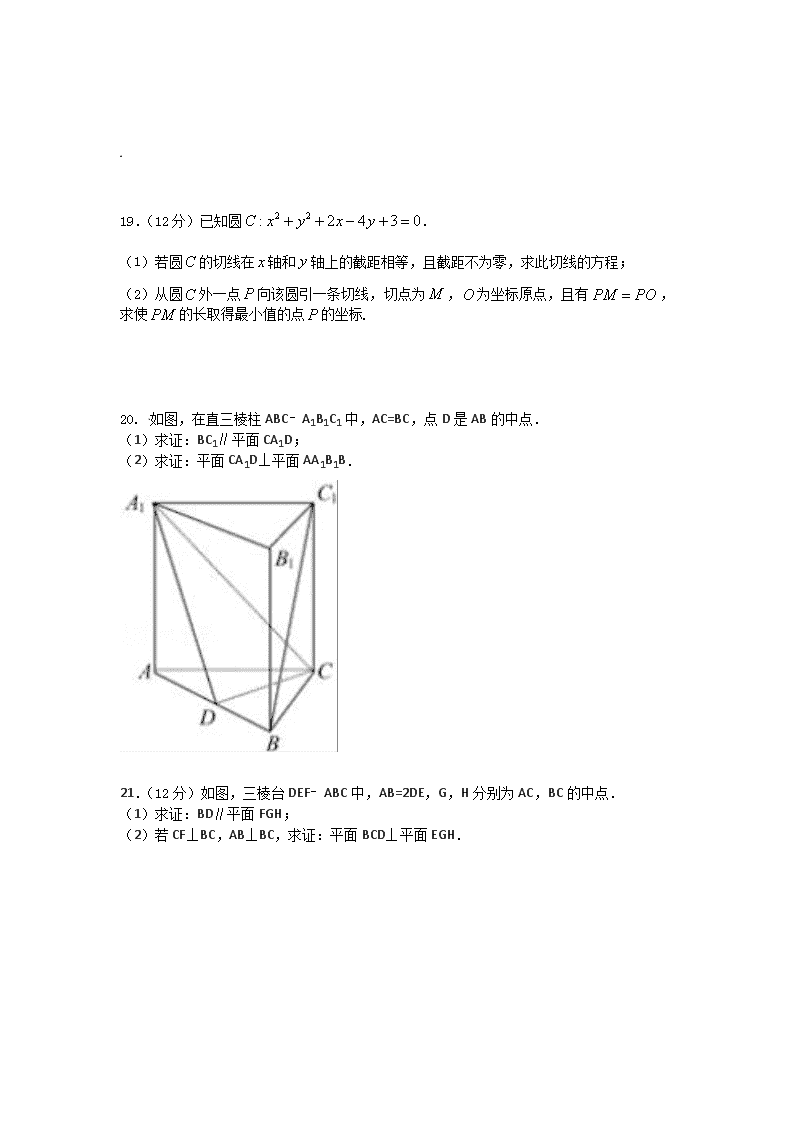‎ ‎18．（12分）如图，三棱柱ABC—A1B‎1C1的侧棱AA1⊥底面ABC，∠ACB = 90°，E是棱CC1上中点，F是AB中点，AC = 1，BC = 2，AA1 = 4.‎ ‎（1）求证：CF∥平面AEB1；‎ ‎（2）求三棱锥A－CB1E的体积.‎ ‎19．（12分）已知圆.‎ ‎（1）若圆的切线在轴和轴上的截距相等，且截距不为零，求此切线的方程；‎ ‎（2）从圆外一点向该圆引一条切线，切点为，为坐标原点，且有，求使的长取得最小值的点的坐标.‎ ‎20. 如图，在直三棱柱ABC﹣A1B‎1C1中，AC=BC，点D是AB的中点．‎ ‎（1）求证：BC1∥平面CA1D；‎ ‎（2）求证：平面CA1D⊥平面AA1B1B．‎ ‎21．（12分）如图，三棱台DEF﹣ABC中，AB=2DE，G，H分别为AC，BC的中点．‎ ‎（1）求证：BD∥平面FGH；‎ ‎（2）若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH．‎ ‎22．（12分）已知圆C过点P（1，1），且与圆M：(x+2)2+(x+2)2=r2(r>0)关于直线x+y+2=0对称．‎ ‎⑴求圆C的方程；‎ ‎⑵设Q为圆C上的一个动点，求的最小值；‎ ‎⑶过点P作两条相异直线分别与圆C相交于A，B，且直线PA和直线PB的倾斜角互补，O为坐标原点，试判断直线OP和AB是否平行？请说明理由．‎ ‎ ‎ ‎　 答案 一．选择题 CBDDDCDCABAC 二．填空题 ‎13. x﹣2y+6=0　．14. x=1或4x﹣3y+5=0 15. 16. ‎ 三．解答题 ‎17．（1）（2）。‎ 试题分析：解、由解得，即点P坐标为，直线的斜率为2‎ ‎（Ⅰ）过点P且平行于直线的直线方程为即；‎ ‎（Ⅱ）过点P且垂直于直线的直线方程为即。‎ ‎18．（1）详见试题解析;（2）‎ 试题解析：（1）证明：取的中点，联结 ‎∵分别是棱、的中点， ∴‎ 又∵ ∴四边形是平行四边形，‎ ‎∴ ∵平面，平面 ∴平面 ‎（2）解： 因为底面，所以底面，‎ 又 ，所以 所以面，即面【来源：全,品…中&高*考+网】‎ 所以点到平面的距离为 ‎ 又因为平面，所以点到平面的距离等于点到平面的距离，即为2‎ 所以.‎ ‎19．（1）或；（2）．‎ 试题解析：（1）切线在两坐标轴上的截距相等且截距不为零，‎ ‎∴设切线方程为（）， 又圆C：，‎ ‎∴圆心C到切线的距离等于圆的半径，∴，解得或，‎ 故所求切线的方程为：或．‎ ‎（2）设， 切线与半径垂直， ∴，‎ ‎∴，整理得，‎ 故动点在直线上，由已知的最小值就是的最小值，‎ 而的最小值为到直线的距离， ‎ ‎∴解得∴所求点坐标为．‎ ‎20. 【解答】解：如图，（1）连接AC1，交A‎1C于点O，连接DO 在△ABC1中，点D是AB的中点，点O是A‎1C的中点 ‎∴BC1∥DO，BC1⊈平面CA1D，DO⊆平面CA1D ‎∴BC1∥平面CA1D ‎（2）∵AC=BC，D是AB的中点 ‎∴CD⊥AB ‎∵直三棱柱ABC﹣A1B‎1C1中，平面AA1B1B⊥平面ABC，平面AA1B1B∩平面ABC=AB ‎∴CD⊥平面AA1B1B，又CD⊂平面CA1D ‎∴平面CA1D⊥平面AA1B1B ‎21． 【解答】（I）证法一：如图所示，连接DG，CD，设CD∩GF=M，连接MH．‎ 在三棱台DEF﹣ABC中，AB=2DE，G为AC的中点．‎ ‎∴，∴四边形CFDG是平行四边形，‎ ‎∴DM=MC．又BH=HC，‎ ‎∴MH∥BD，又BD⊄平面FGH，MH⊂平面FGH，‎ ‎∴BD∥平面FGH；‎ 证法二：在三棱台DEF﹣ABC中，AB=2DE，H为BC的中点．‎ ‎∴，‎ ‎∴四边形BHFE为平行四边形．‎ ‎∴BE∥HF．‎ 在△ABC中，G为AC的中点，H为BC的中点，‎ ‎∴GH∥AB，又GH∩HF=H，‎ ‎∴平面FGH∥平面ABED，‎ ‎∵BD⊂平面ABED，∴BD∥平面FGH．‎ ‎（II）证明：连接HE，∵G，H分别为AC，BC的中点，‎ ‎∴GH∥AB，‎ ‎∵AB⊥BC，∴GH⊥BC，‎ 又H为BC的中点，∴EF∥HC，EF=HC．‎ ‎∴EFCH是平行四边形，∴CF∥HE．‎ ‎∵CF⊥BC，∴HE⊥BC．‎ 又HE，GH⊂平面EGH，HE∩GH=H，‎ ‎∴BC⊥平面EGH，又BC⊂平面BCD，‎ ‎∴平面BCD⊥平面EGH．‎ ‎22．（1）；（2）-4；（3）OP∥AB；理由祥见解析．‎ 试题解析：（1）设圆Ｃ的圆心Ｃ的坐标为(x0,y0）,由于圆M的圆心M(-2,-2),则有:,所以圆C的方程为:,又因为圆C过点P（1，1）,所以有,故知:⊙C的方程为：‎ ‎（2）设Q（x、y），则，从而可设 则【来源：全,品…中&高*考+网】‎ 所以的最小值为-4.‎ ‎（3）设PA的方程为：，则PB的方程为：‎ 由得，同理可得：‎ OP∥AB．‎