浙江省金华十校2018-2019学年高二下学期期末调研考试数学试题 21页

金华十校2018-2019学年高二下学期期末调研考试 数学试题 本试卷分第Ⅰ卷和第Ⅱ卷两部分。考试时间120分钟．试卷总分为150分．请考生按规定用笔将所有试题的答案涂，写在答题纸上.‎ 参考公式：‎ 球的表面积公式 棱柱的体积公式 ‎ ‎ 球的体积公式 其中S表示棱柱的底面积，h表示棱柱的高。‎ ‎ 棱台的体积公式 其中R表示球的半径 ‎ 棱锥的体积公式 其中、表示棱台的上、下底面积，h表示棱 ‎ 台的高.‎ 其中S表示棱锥的底面积，h表示棱锥的高。‎ 一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.已知集合，，则（）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 先求集合，再求两个集合的交集.‎ ‎【详解】，.‎ 故选B.‎ ‎【点睛】本题考查了集合的交集，属于简单题型.‎ ‎2.函数是（）‎ A. 偶函数且最小正周期为2 B. 奇函数且最小正周期为2‎ C. 偶函数且最小正周期为 D. 奇函数且最小正周期为 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 首先化简为，再求函数的性质.‎ ‎【详解】‎ ‎ ，是偶函数，‎ ‎ ‎ 故选C.‎ ‎【点睛】本题考查了三角函数的基本性质，属于简单题型.‎ ‎3.双曲线与双曲线有相同的（）‎ A. 顶点 B. 焦点 C. 渐近线 D. 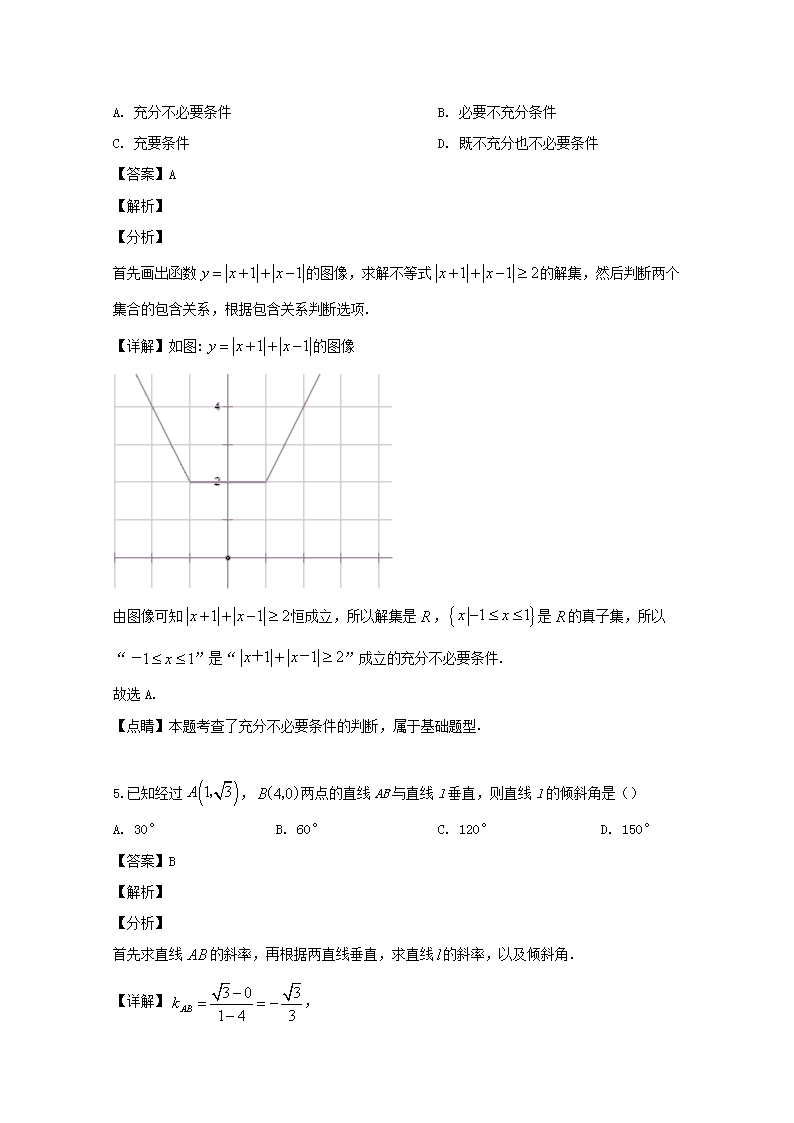离心率 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据选项分别写出两个双曲线的几何性质，比较后得到答案.‎ ‎【详解】的顶点是，焦点是，渐近线方程是，离心率是；的顶点是，焦点是，渐近线方程是，离心率，比较后可知只有渐近线方程一样.‎ 故选C.‎ ‎【点睛】本题考查了双曲线的几何性质，属于简单题型.‎ ‎4.“”是“”成立的（）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 首先画出函数的图像，求解不等式的解集，然后判断两个集合的包含关系，根据包含关系判断选项.‎ ‎【详解】如图:的图像 由图像可知恒成立，所以解集是，是的真子集，所以“”是“”成立的充分不必要条件.‎ 故选A.‎ ‎【点睛】本题考查了充分不必要条件的判断，属于基础题型.‎ ‎5.已知经过，两点的直线AB与直线l垂直，则直线l的倾斜角是（）‎ A. 30° B. 60° C. 120° D. 150°‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 首先求直线的斜率，再根据两直线垂直，求直线的斜率，以及倾斜角.‎ ‎【详解】，‎ ‎，‎ ‎，‎ 直线l的倾斜角是.‎ 故选B.‎ ‎【点睛】本题考查了两直线垂直的关系，以及倾斜角和斜率的基本问题，属于简单题型.‎ ‎6.设，是两个不重合的平面，，是空间两条不重合的直线，下列命题不正确的是（）‎ A. 若，，则 B. 若，，则 C. 若，，则 D. 若，，则 ‎【答案】D ‎【解析】‎ ‎【分析】‎ 选项逐一分析，得到正确答案.‎ ‎【详解】A.正确，垂直于同一条直线的两个平面平行；‎ B.正确，垂直于同一个平面的两条直线平行；‎ C.正确，因为平面内存在直线，使，若，则，则；‎ D.不正确，有可能.‎ 故选D.‎ ‎【点睛】本题重点考查了平行和垂直的概念辨析问题，属于简单题型.‎ ‎7.函数向右平移个单位后得到函数，若在上单调递增，则的取值范围是（）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 首先求函数，再求函数的单调递增区间，区间是函数单调递增区间的子集，建立不等关系求的取值范围.‎ ‎【详解】,‎ 令 ‎ 解得 ， ‎ 若在上单调递增，‎ ‎ ,解得： ‎ ‎ ‎ 时，‎ 故选D.‎ ‎【点睛】本题考查了三角函数的性质和平移变换，属于中档题型.‎ ‎8.已知，，，则（）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据对数运算法则，三个数都化为以2为底的对数，这样就可以比较真数，即比较， ， 的大小，然后再求这三个数的12次方，比较大小.‎ ‎【详解】, ， ，‎ ‎ ，，，‎ ‎，‎ ‎ ，‎ 故选A.‎ ‎【点睛】本题考查了对数比较大小，考查了转化与化归的思想，属于中档题型.‎ ‎9.如图，在菱形ABCD中，，线段AD，BD，BC的中点分别为E，F，K，连接EF，FK．现将绕对角线BD旋转，令二面角A－BD－C的平面角为，则在旋转过程中有（）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 首先根据旋转前后的几何体，表示和，转化为在两个有公共底边的等腰三角形比较顶角的问题，还需考虑和两种特殊情况.‎ ‎【详解】如图，‎ 绕旋转形成以圆为底面两个圆锥，(为圆心，为半径，为 的中点)，，，‎ 当且时，与等腰中，为公共边，，‎ ‎,‎ ‎.‎ 当时，,‎ 当时，,‎ 综上，。‎ C.D选项比较与的大小关系，如图即比较与的大小关系，根据特殊值验证：‎ 又当时，,‎ 当时， ，‎ 都不正确.‎ 故选B.‎ ‎【点睛】本题考查了二面角的相关知识，考查空间想象能力，难度较大，本题的难点是在动态的旋转过程中，如何转化和，从而达到比较的目的，或考查和两种特殊情况，可快速排除选项.‎ ‎10.已知函数，若，均在［1，4］内，且，，则实数的取值范围是（）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 先求导，利用函数的单调性，结合，确定;再利用，即，可得，，设，，确定在上递增，在有零点，即可求实数的取值范围．‎ ‎【详解】解：，‎ 当时， 恒成立，则f（x）在（0，+∞）上递增，则f（x）不可能有两个相等的函数值．故；‎ 由题设， 则 ＝‎ 考虑到，即 ‎，‎ 设，，‎ 则 在上恒成立，‎ 在上递增，在有零点，则 ‎ ， ，‎ ‎ ‎ 故实数的取值范围是．‎ ‎【点睛】本题考查了通过构造函数，转化为函数存在零点，求参数取值范围的问题，本题的难点是根据已知条件，以及，变形为，，然后构造函数转化为函数零点问题.‎ 二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．‎ ‎11.已知，若方程表示圆，则圆心坐标为____；的取值范围是____．‎ ‎【答案】 (1). (2). ‎ ‎【解析】‎ ‎【分析】‎ 当圆的方程是以一般方程给出时，根据圆心坐标公式,还需满足表示圆.‎ ‎【详解】（1）若方程表示圆，那么根据圆心坐标公式，可得，，‎ 圆心坐标.‎ ‎（2）若方程表示圆，那么需满足，即.‎ 故填：;.‎ ‎【点睛】本题考查了圆的一般方程，属于简单题型.‎ ‎12.已知角的终边在直线上，则____；____．‎ ‎【答案】 (1). 1 (2). 1‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据三角函数的定义直接求结果；‎ ‎（2）转化为关于的齐次分式，上下同时除以，计算得结果.‎ ‎【详解】（1） ；‎ ‎（2）.‎ 故填：1；1.‎ ‎【点睛】本题考查了三角函数的定义和的齐次分式求解的问题，属于简单题型.‎ ‎13.已知等比数列的前项和为，，则 ‎（1）____；‎ ‎（2）比较大小：____（填，或）．‎ ‎【答案】 (1). 1 (2). ‎ ‎【解析】‎ ‎【分析】‎ ‎（1）代入，可求出数列的前三项，根据公式，求得；‎ ‎（2）利用基本不等式和等比数列的基本性质得到结论.‎ ‎【详解】（1）当时，，‎ 当时，，解得：，‎ 当时，，解得，‎ 数列是等比数列，‎ ‎，解得；‎ ‎（2）是等比数列，‎ ‎ ‎ ‎ ，‎ ‎ ，‎ ‎，‎ ‎.‎ 故填：1；.‎ ‎【点睛】本题考查了等比数列的性质和基本不等式的简单综合问题，属于简单题型.‎ ‎14.已知向量，．若时，，则____；若对任意 ‎，，则____．‎ ‎【答案】 (1). (2). 0‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据向量平行的坐标表示的公式可得结果，（2）根据已知可得，经过向量数量积的运算，代入坐标得到结果.‎ ‎【详解】（1）根据，，，‎ ‎ ‎ 解得：；‎ ‎（2） ‎ ‎ ‎ ‎，‎ 解得：.‎ 故选：；.‎ ‎【点睛】本题考查了向量共线的坐标表示，和向量数量积的坐标表示，属于简单题型.‎ ‎15.已知，函数，若在区间上单调递减，则的取值范围是____．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据已知可得，恒成立，根据二次函数的图像，列不等式组解决问题.‎ ‎【详解】,‎ 在区间上单调递减，‎ ‎ ，解得.‎ 故填：.‎ ‎【点睛】本题考查了已知函数在某区间的单调性求参数的取值范围，根据函数是单调递减，转化为恒成立，根据二次函数的图像列不等式组，得到参数的取值范围，一般恒成立的问题也可转化为参变分离的方法，转化为求函数的最值问题.‎ ‎16.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为__．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由三视图可分析，几何体应是相同的两个三棱锥，并排放置，并且三棱锥的某个顶点的三条棱两两垂直，根据图中数据直接计算体积.‎ ‎【详解】由三视图可分析，几何体应是相同的两个三棱锥，并排放置，并且三棱锥的某个顶点的三条棱两两垂直，‎ ‎.‎ 故填：.‎ ‎【点睛】本题考查了根据三视图计算几何体的体积，属于简单题型.‎ ‎17.已知平面向量满足，，则的最大值是____．‎ ‎【答案】2‎ ‎【解析】‎ ‎【分析】‎ 根据已知条件可设出的坐标，设，，，利用向量数量积的坐标表示，即求的最大值，根据，可得出的轨迹方程，从而求出最大值.‎ ‎【详解】设，， ‎ ‎ ，‎ ‎ ‎ ‎，‎ 点是以为圆心，1为半径的圆，，‎ ‎， ‎ 的最大值是2.‎ 故填：2.‎ ‎【点睛】本题考查了向量数量积的应用，以及轨迹方程的综合考查，属于中档题型，本题的关键是根据条件设出坐标，转化为轨迹问题.‎ 三、解答题：本大题共5小题，共74分．‎ ‎18.在中，角所对的边分别为．已知．‎ ‎（1）若，，求的面积；‎ ‎（2）求的取值范围．‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据正弦定理和利用，得到，最后求面积；（2）由已知可得，所以，转化为三角函数恒等变形，得到， 根据角的范围求函数的取值范围.‎ ‎【详解】解：（1）在中，∵，∴，‎ ‎∵，，由正弦定理得：，∴，‎ ‎∴，，‎ ‎∴．‎ ‎（2）.‎ ‎∵，∴.‎ ‎∴，则.‎ ‎【点睛】本题考查了利用正余弦定理解三角形，和三角恒等变换求函数的最值，第一问也可利用余弦定理求边，利用求面积.‎ ‎19.如图，在四棱锥中，是以为斜边的直角三角形，，，，．‎ ‎（1）若线段上有一个点，使得平面，请确定点的位置，并说明理由；‎ ‎（2）若平面平面，求直线与平面所成角的正弦值．‎ ‎【答案】（1）当P为AD的中点时，平面PBE（2）‎ ‎【解析】‎ ‎【分析】‎ 要证线面平行，需证明线线平行，所以取中点，连接，即证明；‎ ‎（2）过B作于H，连结HE，证明两两垂直，以点为原点，建立空间直角坐标系，求平面的法向量，利用公式求解.‎ ‎【详解】解：（1）当P为AD的中点时，，‎ 又因为平面PBE，平面PBE，所以平面PBE．‎ ‎（2）过B作于H，连结HE，在等腰梯形ABCD中易知．‎ 中，，，，可得．‎ 又因为，平面平面ADE，‎ 且平面平面，‎ 所以平面ADE，所以．‎ 如图，以H为原点，HE，HD，HB所在直线分别为x轴，y轴，z轴建立空间直角坐标系.‎ 则，，，.‎ 所以，.．设平面ABE的一个法向量，‎ 则，即，取，得.‎ 设直线CD与平面ABE所成角为，所以.‎ ‎【点睛】本题重点考查了线面角的求法，坐标法的一个难点是需建立空间直角坐标系，这个过程往往需要证明，证明后再建立空间直角坐标系，利用公式求解.‎ ‎20.已知等差数列的公差为，等比数列的公比为，若，且，，，成等差数列．‎ ‎（1）求数列，的通项公式；‎ ‎（2）记，数列的前项和为，数列的前项和为，若对任意正整数，恒成立，求实数的取值范围．‎ ‎【答案】（1），（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）分别根据，和成等差数列，分别表示为和的方程组，求出首项，即得通项公式；（2）根据（1）的结果可求得，并且求出,利用裂项相消法求和，转化为，恒成立，转化为求数列的最值.‎ ‎【详解】解：（1）因为，，成等差数列，所以①，‎ 又因为，，成等差数列，所以，得②，‎ 由①②得，．所以，.‎ ‎（2），.‎ ‎.‎ 令，则，‎ 则，‎ 所以，当时，，当时，‎ 所以的最小值为.‎ 又恒成立，所以，．‎ ‎【点睛】本题考查了数列通项的求法，和求数列的前项和的方法，以及和函数结合考查数列的最值，尤其在考查数列最值时，需先判断函数的单调性，判断的正负，根据单调性求函数的最值.‎ ‎21.已知椭圆的离心率为，抛物线与椭圆在第一线象限的交点为．‎ ‎（1）求曲线、的方程；‎ ‎（2）在抛物线上任取一点，在点处作抛物线的切线，若椭圆上存在两点关于直线对称，求点的纵坐标的取值范围．‎ ‎【答案】（1），（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据离心率可得，再将点分别代入两个曲线，求得曲线方程；（2‎ ‎）首先设，根据导数的几何意义求切线的方程，设椭圆上关于l对称的两点为，，那么设直线的方程，，转化为直线与椭圆有交点，并且的中点落在切线上的问题，最后根据，求得的范围.‎ ‎【详解】解：（1）由已知得：，所以．把代入椭圆，‎ 解得，所以，得椭圆．‎ 把代入抛物线得，‎ 所以抛物线．‎ ‎（2）设点，抛物线，所以，所以切线.‎ 设椭圆上关于l对称的两点为，.‎ ‎（1）当时，设直线 代入椭圆得：．‎ ‎，化简得.……（*）‎ ‎，所以MN的中点Q的横坐标，纵坐标.‎ 要使M，N关于直线l对称，则点Q在直线l上，即，‎ 化简得：，代入（*）式解得.‎ ‎（2）当时，显然满足要求.‎ 综上所述：，所以点P的纵坐标的取值范围是.‎ ‎【点睛】本题考查了求曲线方程，以及直线与圆锥曲线的位置关系的问题，考查了转化与化归，以及计算能力，属于中档题型.‎ ‎22.已知函数．‎ ‎（1）求函数的最小值；‎ ‎（2）当时，记函数的所有单调递增区间的长度为，所有单调递减区间的长度为，证明：．（注：区间长度指该区间在轴上所占位置的长度，与区间的开闭无关．）‎ ‎【答案】（1）（2）见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）首先求函数的导数，然后判断函数的单调性，最后求最值；‎ ‎（2）根据（1）首先求函数的零点，从而去掉的绝对值，分段求函数的单调区间，最后再比较单调区间的长度.‎ ‎【详解】解（1）因为，所以在单调递减，单调递增，‎ 所以.‎ ‎（2）由（1）可知，在单调递减，单调递增 又，，‎ 所以存在，使得，‎ 则当时，，当时，‎ 所以，‎ 记，‎ 当时，，所以 在单调递增，在单调递减.‎ 当或时，‎ 当时即在单调递增.‎ 因为，所以 则当时，令，有 所以当时，，在单调递减 综上，在与单调递减，在与单调递增.‎ 所以，又 所以，即 ‎【点睛】本题考查了利用函数的导数研究函数的单调性，属于中档题型，本题的一个难点是函数的零点，其中一个是，另一个不确定，只能估算其范围，设为，所以再求当或时，函数的单调区间时，也需估算比较的范围，确定时函数的减区间，这种估算零点存在性问题，是导数常考题型.‎ ‎ ‎ ‎ ‎