- 508.50 KB
- 2021-06-01 发布
绝密★启用前
2017-2018学年云南省昆明市黄冈实验学校高二上学期期中考试数学(理)试题 解析版
注意事项.
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
评卷人
得分
一、选择题(题型注释)
1、(本题5分)若实数满足,则的最大值为( )
A. B. C. D.
2、(本题5分)命题“∀x>0,都有x2﹣x+3≤0”的否定是( )
A.∃x>0,使得x2﹣x+3≤0 B.∃x>0,使得x2﹣x+3>0
C.∀x>0,都有x2﹣x+3>0 D.∀x≤0,都有x2﹣x+3>0
3、(本题5分)设全集为R,函数的定义域为M,则= ( )
A. B. C. D.
4、(本题5分)三角形全等是三角形面积相等的
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
5、(本题5分)不等式的解集为
A. B. C. D.∪
6、(本题5分)设、为正数,则的最小值为( )
A. B. C. D.
7、(本题5分)设集合,集合,则( ).
A. B. C. D.
8、(本题5分)椭圆上的一点到左焦点的距离为2,是的中点,则为( )
A.2 B.4 C.8 D.
9、(本题5分)与曲线共焦点,且渐近线为的双曲线的方程为( )
A. B. C. D.
10、(本题5分)书架上有2本不同的语文书,1本数学书,从中任意取出2本,取出的书恰好都是语文书的概率为( )
A. B. C. D.
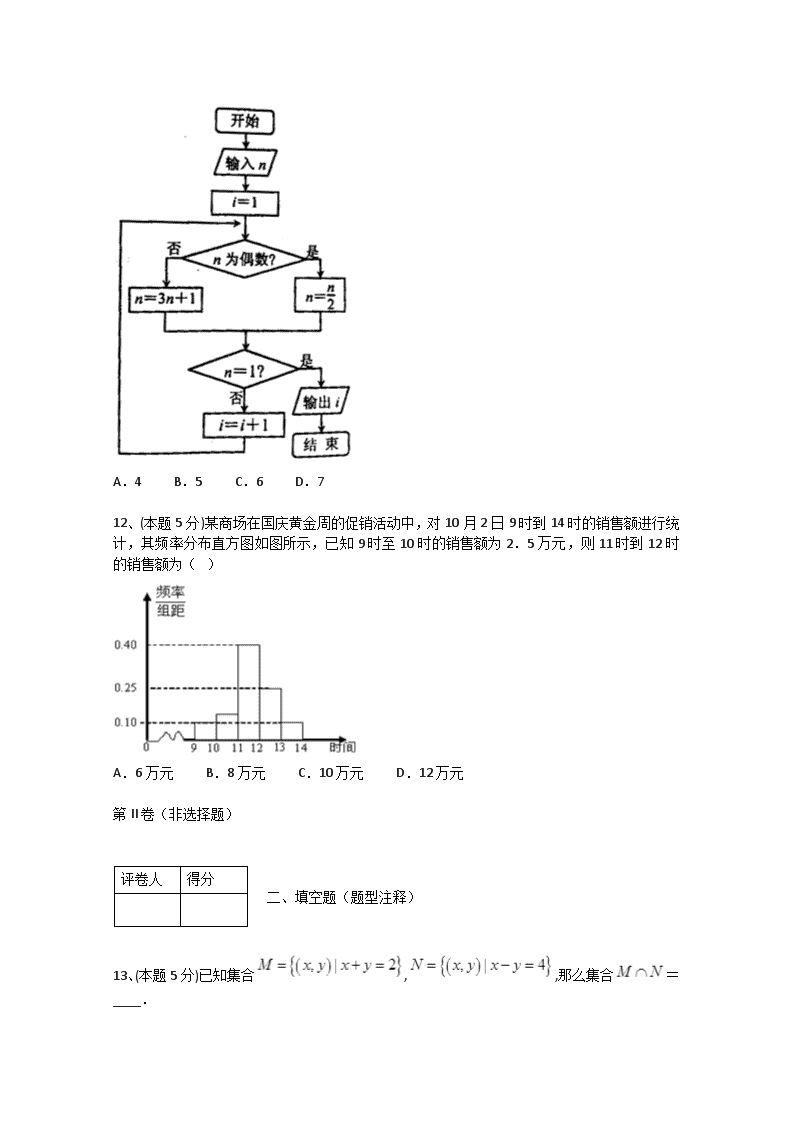
11、(本题5分)执行如图所示的程序框图,若输入的,则输出的结果为( )
A.4 B.5 C.6 D.7
12、(本题5分)某商场在国庆黄金周的促销活动中,对10月2日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为( )
A.6万元 B.8万元 C.10万元 D.12万元
第II卷(非选择题)
评卷人
得分
二、填空题(题型注释)
13、(本题5分)已知集合,,那么集合=____.
14、(本题5分)已知命题,则对应的集合为___________.
15、(本题5分)在区间上随机地取一个数,则“”的概率为__________.
16、(本题5分)双曲线(a>0)的离心率为______.
评卷人
得分
三、解答题(题型注释)
17、(本题12分)某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(1)求频率分布图中的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率..
18、(本题12分)(本题满分10分)
命题p:“方程表示焦点在y轴上的椭圆”,
命题q:“,恒成立”,
若命题p与命题q有且只有一个是真命题,求实数的取值范围。
19、(本题12分)已知椭圆的短轴长为,离心率.
求椭圆的标准方程;
20、(本题12分)已知双曲线与椭圆有相同的焦点,实半轴长为.
(1)求双曲线的方程;
21、(本题12分)某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示.
(1)求甲、乙两名运动员得分的中位数;
(2)你认为哪位运动员的成绩更稳定?
(3)如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分,求甲的得分大于乙的得分的概率.
22、(本题10分)
2013年春节前,有超过20万名广西、四川等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年,为防止摩托车驾驶人因长途疲劳驾驶,手脚僵硬影响驾驶操作而引发交事故,肇庆市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾乘人员休息站,让过往返乡过年的摩托车驾驶人有一个停车休息的场所。交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车就进行省籍询问一次,询问结果如图所示:
(1)问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法?
(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的有5名,则四川籍的应抽取几名?
2017-2018学年云南省昆明市黄冈实验学校高二上学期期中考试数学(理)试题
评卷人
得分
一、选择题(题型注释)
1、(本题5分)设集合,集合,则( ).
A.
B.
C.
D.
来源:2016-2017北京西城13中高一上期中数学试题
【答案】B
【解析】集合,,∴.故选.
点晴:集合的三要素是:确定性、互异性和无序性.研究一个集合,我们首先要看清楚它的研究对象,是实数还是点的坐标还是其它的一些元素,这是很关键的一步.集合与集合间有包含关系. 在求交集时注意区间端点的取舍. 熟练画数轴来解交集、并集和补集的题目.
2、(本题5分)若实数满足,则的最大值为( )
A.
B.
C.
D.
来源:【百强校】2017届四川绵阳市高三一诊考试数学(文)试卷(带解析)
【答案】C
【解析】
试题分析:可行域为一个三角形ABC及其内部,其中,所以直线过点B时取最大值2,选C.
考点:线性规划
【易错点睛】线性规划的实质是把代数问题几何化,即数形结合的思想.需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最大或最小值会在可行域的端点或边界上取得.
3、(本题5分)设全集为R,函数的定义域为M,则= ( )
A.
B.
C.
D.
来源:福建省德化一中、永安一中、漳平一中2017-2018学年高一上学期三校联考数学试题
【答案】C
【解析】由题意, 故M=,所以=.
故选C
4、(本题5分)三角形全等是三角形面积相等的
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条件
来源:【全国市级联考】四川省内江市2016-2017学年高二下学期期末检测数学(理)试题
【答案】A
【解析】当三角形的面积相等时,三角形不一定全等,但是三角形全等时面积一定相等.
即:三角形全等是三角形面积相等的充分但不必要条件.
本题选择A选项.
5、(本题5分)不等式的解集为
A.
B.
C.
D.∪
来源:【全国市级联考】湖南省张家界市2015-2016学年高一下学期期末联考数学(A)试题
【答案】B
【解析】由得,即,故选B.
6、(本题5分)设、为正数,则的最小值为( )
A.
B.
C.
D.
来源:2012-2013年云南大理宾川第四高级中学高二下开学考试理科数学试题(带解析)
【答案】B
【解析】
试题分析:,当且仅当即时等号成立,所以最小值为9
考点:均值不等式
点评:利用均值不等式求最值时要注意其成立的条件:都是正数,当和为定值时,乘积取最值,当乘积为定值时,和取最值,最后验证等号成立的条件是否满足
7、(本题5分)命题“∀x>0,都有x2﹣x+3≤0”的否定是( )
A.∃x>0,使得x2﹣x+3≤0
B.∃x>0,使得x2﹣x+3>0
C.∀x>0,都有x2﹣x+3>0
D.∀x≤0,都有x2﹣x+3>0
来源:河南省商丘市第一高级中学2017-2018学年高二10月月考数学(理)试题
【答案】B
【解析】命题都有的否定是:
使得
故选
8、(本题5分)椭圆上的一点到左焦点的距离为2,是的中点,则为( )
A.2
B.4
C.8
D.
来源:【全国百强校word】四川省绵阳市南山中学实验学校2016-2017学年高二上学期半期考试数学(文)试题
【答案】B
【解析】根据椭圆定义,为的中点,则为的中位线,所以,故选择B.
9、(本题5分)与曲线共焦点,且渐近线为的双曲线的方程为( )
A.
B.
C.
D.
来源:【全国百强校word】四川省绵阳市南山中学实验学校2016-2017学年高二上学期半期考试数学(文)试题
【答案】A
【解析】椭圆的焦点为,排除B,D选项,又焦点在上的双曲线的渐近线方程为,故选择A.
10、(本题5分)书架上有2本不同的语文书,1本数学书,从中任意取出2本,取出的书恰好都是语文书的概率为( )
A.
B.
C.
D.
来源:【全国百强校】甘肃省高台县第一中学2016-2017学年高二下学期期末考试数学(文)试题
【答案】A
【解析】从 本不同的语文书, 本数学书,从中任意取出本,共=3种取法,恰好都是语文书的取法只有种,所以概率为,故选A.
11、(本题5分)执行如图所示的程序框图,若输入的,则输出的结果为( )
A.4
B.5
C.6
D.7
来源:河北省唐山市2016-2017学年度高三年级第二次模拟考试文科数学试题
【答案】B
【解析】由程序框图,得
结束循环,输出值,即;故选B.
12、(本题5分)某商场在国庆黄金周的促销活动中,对10月2日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为( )
A.6万元
B.8万元
C.10万元
D.12万元
来源:福建省2016届高三基地校总复习综合卷数学试题(厦门双十、南安一中、厦门海沧实验中学文科)
【答案】C
【解析】设11时到12时的销售额为万元,依题意有,,故选C.
点睛:利用频率分布直方图求众数、中位数与平均数时,易出错,应注意区分这三者.在频率分布直方图中:
(1)最高的小长方形底边中点的横坐标即是众数;
(2)中位数左边和右边的小长方形的面积和是相等的;
(3)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
第II卷(非选择题)
请点击修改第II卷的文字说明
评卷人
得分
二、填空题(题型注释)
13、(本题5分)已知集合,,那么集合=____.
来源:【全国百强校】江西省赣州市崇义中学2017-2018学年高一上学期第一次月考数学试题
【答案】{(3,-1)}
【解析】由条件知指的是两条直线的交点的坐标,
故结果为{(3,-1)}.
14、(本题5分)已知命题,则对应的集合为___________.
来源:【百强校】2017届江西鹰潭一中高三上学期月考二数学(理)试卷(带解析)
【答案】
【解析】
试题分析:,因此为.
考点:命题的否定.
15、(本题5分)在区间上随机地取一个数,则“”的概率为__________.
来源:【全国市级联考】山东省枣庄市2016-2017学年高一下学期期末考试数学试题
【答案】
【解析】 ;
, 区间长
所以概率为: .
16、(本题5分)双曲线(a>0)的离心率为______.
来源:【全国百强校】]广西钦州市钦州港经济技术开发区中学2017-2018学年高二上学期开学考试数学(文)试题
【答案】
【解析】双曲线 (a>0)的,
,
即有
故选A.
评卷人
得分
三、解答题(题型注释)
17、(本题12分)某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(1)求频率分布图中的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率..
来源:【全国百强校】安徽省阜阳市临泉县第一中学2016-2017学年高一下学期学科竞赛数学(文)试题
【答案】(1); (2)
【解析】试题分析:(1)利用频率分布直方图中的信息,所有矩形的面积和为1,得到a; (2)从评分在的受访职工中都在的人数,随机抽取2人,列举法求出所有可能,利用古典概型公式解答.
试题解析:(1)由频率分布直方图知,
所以.
该企业的职工对该部分评分不低于80的概率为.
(2)在的受访职工人数为,
此2人评分都在的概率为.
18、(本题12分)(本题满分10分)
命题p:“方程表示焦点在y轴上的椭圆”,
命题q:“,恒成立”,
若命题p与命题q有且只有一个是真命题,求实数的取值范围。
来源:2011-2012年福建省福州市八中高二上学期期末考试文科数学
【答案】
解:命题p为真命题时, …………2分
命题q为真命题时, …………5分
命题p为真,命题q为假 ……7分
命题p为假,命题q为真 ……9分
综上述,的取值范围是 …………10分
【解析】略
19、(本题12分)已知椭圆的短轴长为,离心率
.
(1)求椭圆的标准方程;
(2)若分别是椭圆的左、右焦点,过的直线与椭圆交于不同的两点,求的内切圆半径的最大值.
来源:【百强校】2017届云南大理州高三理上学期统测一数学试卷(带解析)
【答案】(1);(2).
【解析】
试题分析:(1)根据题意列出待定系数的方程组,即可求得方程;(2)设的内切圆的半径为,
易得的周长为,所以,因此最大,就最大. 把分解为和,从而得到,整理方程组, 求出两根和与两根既即得到面积与的函数关系,通过换元,利用均值不等式即可求得的最大值,此时.
试题解析:(1)由题意可得...................2分
解得..................3分
故椭圆的标准方程为..................... 4分
(2)设,设的内切圆的半径为,
因为的周长为,,
因此最大,就最大........................6分
,
由题意知,直线的斜率不为零,可设直线的方程为,
由得,
所以,.................8分
又因直线与椭圆交于不同的两点,
故,即,则
............10分
令,则,
.
令,由函数的性质可知,函数在上是单调递增函数,
即当时,在上单调递增,
因此有,所以,
即当时,最大,此时,
故当直线的方程为时,内切圆半径的最大值为...........12分
考点:椭圆的标准方程、直线与椭圆的位置关系.
【方法点晴】本题主要考查了椭圆的标准方程、直线与椭圆的位置关系,考查了待定系数法、转化的思想方法和函数的思想,属于中档题.求椭圆方程要注意的关系
,本题解答的关键是第(2)中,把的内切圆半径最大转化为其面积的最大值,通过分解其面积,表示出面积与参数的函数关系,通过换元,最后根据均值不等式求出其最大值.
20、(本题12分)已知双曲线与椭圆有相同的焦点,实半轴长为.
(1)求双曲线的方程;
(2)若直线与双曲线有两个不同的交点和,且(其中为原点),求的取值范围.
来源:2016-2017学年广东清远清城区三中高二文上学期第二次月考数学试卷(带解析)
【答案】(1)(2)
【解析】
试题分析:(1)设双曲线的方程为 (a>0,b>0),由已知易求a,c,根据a,b,c的平方关系即可求得b值;(2)设A,B,则由,可得
,联立方程组消掉y,根据韦达定理即可得到关于k的不等式,注意判别式大于0,解出即得k的范围
试题解析:(1)解:设双曲线的方程为,
故双曲线方程为.
(2)解:将代入得
由得且 设,则由得
=
,得
又,,即
考点:直线与圆锥曲线的关系;双曲线的标准方程
21、(本题12分)某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示.
(1)求甲、乙两名运动员得分的中位数;
(2)你认为哪位运动员的成绩更稳定?
(3)如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分,求甲的得分大于乙的得分的概率.
来源:【全国百强校】河北省正定中学2016-2017学年高二下学期第四次月考(期末)数学(文)试题
【答案】(1)甲运动员得分的中位数为22,乙运动员得分的中位数为23.;(2)甲运动员的成绩更稳定;
(3)
【解析】试题分析:(1)由茎叶图中茎表示十位数,叶表示个数数,我们可以列出甲、乙两名篮球运动员各场的得分,进而求出甲、乙两名运动员得分的中位数;(2)由表中数据,我们易计算出甲、乙两名篮球运动员各场的得分的方差,,然后比较,根据谁的方差小谁的成绩稳定的原则进行判断;(3)我们计算出从甲、乙两位运动员的7场得分中各随机抽取一场的得分的基本事件总数,然后再计算出其中甲的得分大于乙的基本事件个数,代入古典概率计算公式,即可求解.
试题解析:(1)甲运动员得分的中位数为22,乙运动员得分的中位数为23.
(2),
,
,
,
∴,从而甲运动员的成绩更稳定.
(3)从甲、乙两位运动员的7场得分中各随机抽取一场的得分的基本事件总数为,其中甲的得分大于乙的是:甲得14分有3场,甲15分有3场,甲得17分有3场,甲得22分有3场,甲得23分有3场,甲得24分有4场,甲得32分有7场,共计26场.
因为,甲的得分大于乙的得分的概率.
22、(本题10分)
23、2013年春节前,有超过20万名广西、四川等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年,为防止摩托车驾驶人因长途疲劳驾驶,手脚僵硬影响驾驶操作而引发交事故,肇庆市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾乘人员休息站,让过往返乡过年的摩托车驾驶人有一个停车休息的场所。交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车就进行省籍询问一次,询问结果如图所示:
(1)问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法?
(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的有5名,则四川籍的应抽取几名?
(3)在上述抽出的驾驶人员中任取2名,求抽取的2名驾驶人员中四川籍人数的分布列及其数学期望。
来源:2013届陕西省三原县北城中学高三第一次月考理科数学题(带解析)
【答案】(1)系统抽样(2)2名
(3)的分布列为:
0
1
2
数学期望
【解析】
试题分析:(1)根据题意因为有相同的间隔,符合系统抽样的特点,
所以交警小李对进站休息的驾驶人员的省籍询问采用的是系统抽样方法. ……3分
(2)从图中可知,被询问了省籍的驾驶人员广西籍的有:人,
四川籍的有:人, ……5分设四川籍的驾驶人员应抽取名,依题意得,解得,
即四川籍的应抽取2名. ……8分
(3) 的所有可能取值为0,1,2;
,,,
的分布列为:
0
1
2
……13分
数学期望. ……14分
考点:本小题主要考查随机抽样,分布列,数学期望.
点评:随机抽样分简单随机抽象,系统抽样,分层抽样三种,各自有各自的特点和适用范围,要灵活选择;写分布列时,要准确求出各自的概率,并通过验证概率和是否是1验证所写分布列是否正确.