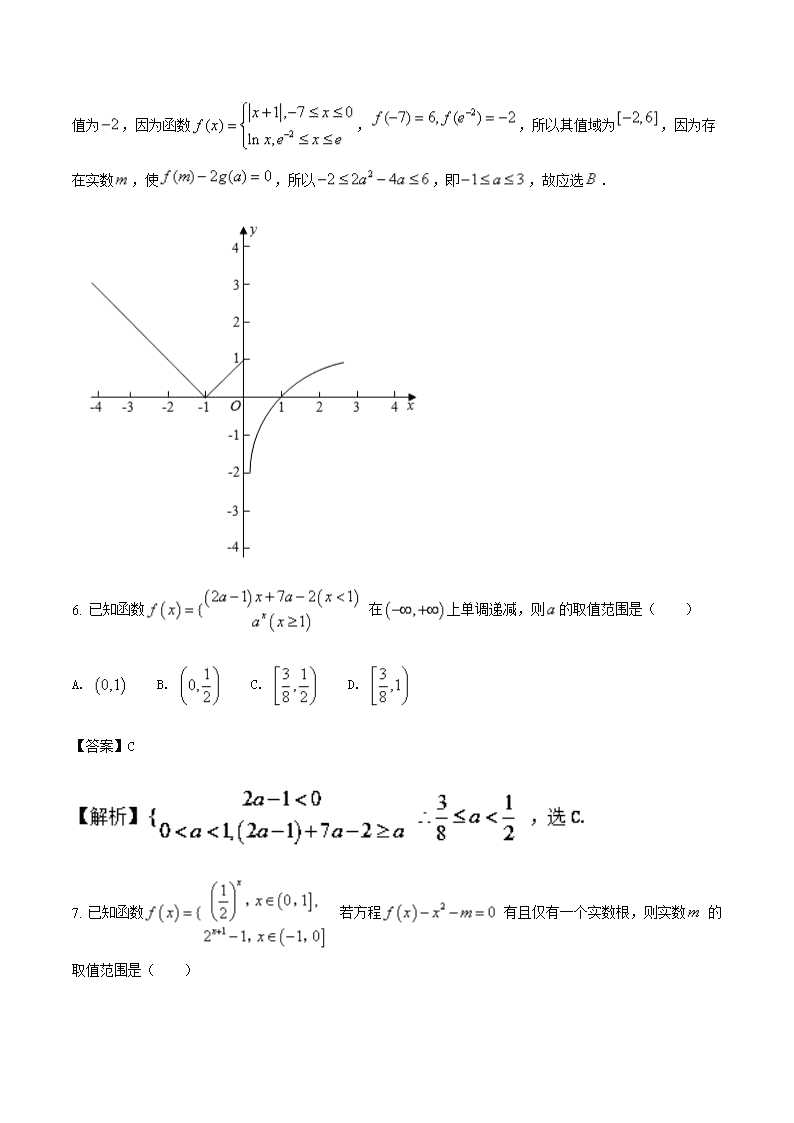专题2-2+基本初等函数中含有参数问题（测）-2018年高考数学（文）二轮复习讲练测 16页

‎2018高三二轮复习之讲练测之测案【新课标版文科数学】‎ 测---能力提升 总分 _______ 时间 _______ 班级 _______ 学号 _______ 得分_______‎ （一） 选择题（12*5=60分）‎ ‎1.命题“，”为真命题的一个充分不必要条件是（ ）‎ A． B． C. D．‎ ‎【答案】C ‎【解析】‎ ‎2.已知函数，若，则（ ）‎ ‎ ‎ ‎【答案】A ‎【解析】‎ 试题分析：因为所以 ‎3. 为参数，函数是偶函数，则可取值的集合是（ ）‎ A．｛0，5｝ B．｛2，5｝ C．｛5，2｝ D．｛1，2015｝‎ ‎【答案】C ‎【解析】‎ 因为函数是偶函数，所以∴，利用系数恒等关系可知．解方程得或，故选C．‎ ‎4.已知是偶函数，它在上是减函数，若，则的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ ‎5.已知函数，，设为实数，若存在实数，使，则实数的取值范围为（ ）‎ A、 B、 C、 D、‎ ‎【答案】B ‎【解析】‎ 因为，为实数，所以，因为，所以当时，‎ 的最小值为，因为函数，，所以其值域为，因为存在实数，使，所以，即，故应选．‎ ‎6. 已知函数在上单调递减，则的取值范围是（　　）‎ A. B. C. D. ‎ ‎【答案】C ‎7. 已知函数 若方程 有且仅有一个实数根，则实数 的取值范围是（ ）‎ A. B. 或 C. D. 或 ‎【答案】D ‎【解析】原问题等价于在区间内只有一个实数根，‎ 即函数与函数的图象在区间内只有一个交点，‎ 据此绘制函数图象如图所示，结合函数图象可知：‎ 或，‎ 由可得，‎ 由可得，‎ 综上可得：实数的取值范围是 或.‎ 本题选择D选项.‎ ‎8.【湖南省长沙市长郡中学2017届高三上学期第三次月考模拟】已知函数，若当时，恒成立，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎9.函数 ，若实数满足，则实数的所有取值的和为（ ）‎ A．1 B． C． D．‎ ‎【答案】C ‎【解析】‎ ‎10. 若是的最小值，则的取值范围为（ ）.‎ ‎ (A)[-1,2] (B)[-1，0] (C)[1，2] (D) ‎ ‎【答案】D ‎【解析】由于当时，在时取得最小值，由题意当时，应该是递减的，则，此时最小值为，因此，解得，选D．‎ ‎11.【河北省武邑中学2017届高三上学期第三次调研】已知定义在上的函数满足:，在区间上，,若,则（ ）‎ A． B． C. D．‎ ‎【答案】A ‎【解析】‎ ‎，故选A.‎ ‎12.【河南省新乡市2017届高三上学期第一次调研测试】已知函数，若，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】‎ 当时，符合题意，排除A，D.当时，不符合题意，排除C，故选B.‎ （一） 填空题（4*5=20分）‎ ‎13.已知函数是定义在上的奇函数，当时，. 若集合，则实数的取值范围为 .‎ ‎【答案】‎ ‎【解析】‎ ‎14. 已知函数满足对任意的，都有恒成立，那么实数 的取值范围是______________‎ ‎【答案】‎ ‎【解析】∵函数f（x）满足对任意x1＜x2，都有f（x1）＜f（x2）成立，∴函数f（x）在定义域上是增函数，则满足, ‎ 故答案为.‎ ‎15.已知函数R， ，若关于的方程为自然对数的底数）只有一个实数根， 则= ．‎ ‎【答案】‎ ‎【解析】‎ ‎16.【2018届北京市西城区高三上学期期末】已知函数，若，则的值域是______；若的值域是，则实数的取值范围是______．‎ ‎【答案】 ‎ 三、解答题（共6道小题，共70分）‎ ‎17.设集合，集合.已知命题 ‎，命题，且命题是命题的必要不充分条件，求实数的取值范围.‎ ‎【答案】.‎ ‎【解析】‎ 由已知得，………………2分 ‎.………………4分 ‎∵是的必要不充分条件，‎ ‎∴.………………6分 则有.………………8分 ‎∴，故的取值范围为.………………10分 ‎18.已知是奇函数．‎ 求的单调区间；‎ 关于的不等式＞有解，求的取值范围.‎ ‎【答案】（Ⅰ）；增区间为，减区间为；（Ⅱ）．‎ ‎【解析】‎ ‎19.已知函数，为常数．‎ ‎（1）当时，求函数在上的最小值和最大值；‎ ‎（2）若函数在上单调递增，求实数的取值范围．‎ ‎【解析】‎ ‎20.【2018届西藏林芝市第一中学高三9月月考】已知函数（， ）．‎ ‎（1）若函数的最小值为，求的解析式，并写出单调区间；‎ ‎（2）在（1）的条件下， 在区间上恒成立，试求的取值范围．‎ ‎【答案】(1) ，单调递减区间为，单调递增区间为 ；‎ ‎(2) 的取值范围为．‎ ‎【解析】试题分析：（１）由函数的最小值为，可知函数的最值和对称轴方程，布列方程，即可求得的解析式；（２）在区间上恒成立转化为在区间上恒成立，求出二次函数的最小值，即可得到的取值范围．‎ 试题解析：‎ ‎（1）由题意得， ，且，‎ ‎∴， ，∴，‎ 单调递减区间为，单调递增区间为．‎ ‎（2）在区间上恒成立，‎ 转化为在区间上恒成立．‎ 设， ，则在上递减，‎ ‎∴，‎ ‎∴，即的取值范围为．‎ ‎21.设函数.‎ ‎(1) 解不等式；‎ ‎(2) 设函数，若函数为偶函数，求实数的值；‎ ‎(3) 当时，是否存在实数（其中），使得不等式恒成立？若存在，求出的取值范围；若不存在，说明理由.‎ ‎【答案】（1）：（2）；（3）不存在．‎ ‎【解析】‎ ‎22.已知函数 （1） 若在上的最大值和最小值分别记为，求；‎ （2） 设若对恒成立，求的取值范围.‎ ‎【答案】（Ⅰ）；（Ⅱ）的取值范围．‎ ‎【解析】‎ ‎；‎ ‎（II）令，则，，因为