- 605.87 KB
- 2021-06-01 发布
2019学年第一学期期末联考
高一数学试卷
【完卷时间:120分钟 满分:150分】
第Ⅰ卷(选择题 共60分)
一、选择题:本大题有12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求.
1.直线的倾斜角为( )
A.60° B.30° C.120° D.150°
2.直线与平行,则的值等于( )
A. -1或3 B.1或3 C.-3 D.-1
3.如图是水平放置的平面图形的斜二测直观图,其原来
平面图形面积是( )
A.2 B.4 C.6 D.8
4.过点且垂直于直线的直线方程为( )
A. B. C. D.
5.已知两平行直线间的距离为3,则
( )
A.-12 B.48 C.36 D.-12或48
6.已知圆O1:x2+y2=1与圆O2:(x﹣3)2+(x+4)2=16,则圆O1与圆O2的位置关
系为( )
A. 外切 B. 内切 C.相交 D.相离
7.设是两条不同的直线,是三个不同的平面.给出下列四个命题:
①若⊥, ,则; ②若,则;
③若,则; ④若,则.
其中正确命题的序号是( )
9
A. ①和② B. ②和③ C.③和④ D.①和④
8.圆上存在两点关于直线对称,则实数的
值为( )
A. 6 B.-4 C.8 D.无法确定
9.体积为4π的球的内接正方体的棱长为( ).
A. B.2 C. D.
10.一空间几何体的三视图如下图所示,则该几何体的体积为( )
A. B. C D.
11.如右图,在三棱柱中,各棱长相等,侧棱垂直于底面,点是侧面的中点,则与平面所成角的大小是( )
A. B. C. D.
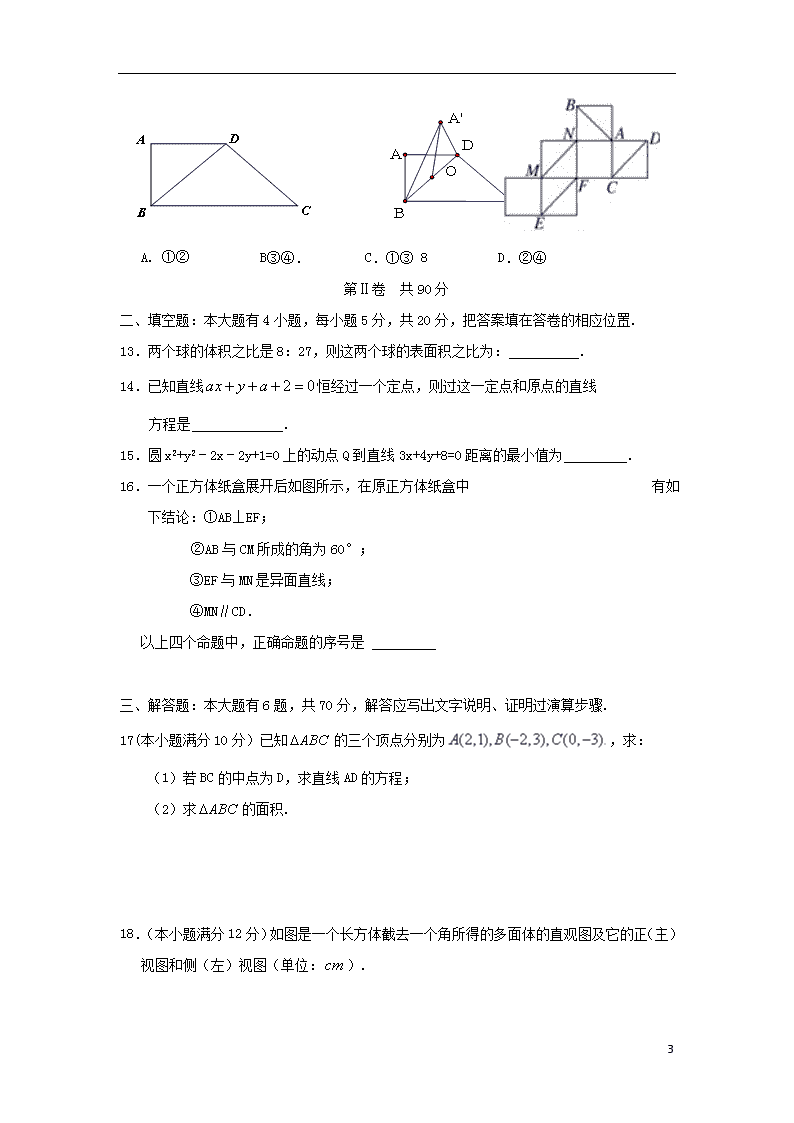
12.如下图,梯形中,∥,,, ,将沿对角线折起.设折起后点的位置为,并且平面平面.给出下面四个命题:
①;②三棱锥的体积为;③平面;
④平面平面.其中正确命题的序号是( )
9
A. ①② B③④. C.①③ 8 D.②④
第Ⅱ卷 共90分
二、填空题:本大题有4小题,每小题5分,共20分,把答案填在答卷的相应位置.
13.两个球的体积之比是8:27,则这两个球的表面积之比为: .
14.已知直线恒经过一个定点,则过这一定点和原点的直线
方程是 .
15.圆x2+y2﹣2x﹣2y+1=0上的动点Q到直线3x+4y+8=0距离的最小值为 .
16.一个正方体纸盒展开后如图所示,在原正方体纸盒中 有如下结论:①AB⊥EF;
②AB与CM所成的角为60°;
③EF与MN是异面直线;
④MN∥CD.
以上四个命题中,正确命题的序号是
三、解答题:本大题有6题,共70分,解答应写出文字说明、证明过演算步骤.
17(本小题满分10分)已知的三个顶点分别为,求:
(1)若BC的中点为D,求直线AD的方程;
(2)求的面积.
18.(本小题满分12分)如图是一个长方体截去一个角所得的多面体的直观图及它的正(主)视图和侧(左)视图(单位:).
9
(1)画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的表面积;(尺寸如图)
19.(本小题满分12分)如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .
(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
20.(本小题满分12分)如右图所示,一座圆拱(圆的一部分)桥,当水面在图位置m时,拱顶离水面2 m,水面宽 12 m,当水面下降1 m后,水面宽多少米?
9
21. (本小题满分12分)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,
AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
22.(本小题满分12分)已知圆,直线,点在直线上,过点作圆的切线、,切点为、.
(1)若,求点坐标;
(2)若点的坐标为,过作直线与圆交于、两点,当时,求直线的方程;
(3)求证:经过、、三点的圆与圆的公共弦必过定点,并求出定点的坐标.
9
福州市八县(市)协作校2016—2017学年第一学期期末联考
高一数学参考答案
一、选择题(每题5分,满分60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
D
D
B
B
D
A
D
A
B
D
C
B
二、填空题(每小题4分, 共20分)
13. 14. 15. 2 16. ①③
三、解答题:
17.(本小题满分10分)
解:(Ⅰ)因为,所以 ............2分
所以直线的方程为 .................4分
整理得: . ................5分
(Ⅱ)因为,所以 ...........7分
又直线的方程为,则到直线的距离为. 所以的面积为. ..............10分
18.(本小题满分12分)
解:(1)该多面体的俯视图如下图所示: ......4分
(2)所求多面体的表面积 S=
9
= ----------(12分)
19.(本小题满分12分)
解:(1)∵AB⊥平面BCD,CD⊂平面BCD,∴AB⊥CD.
又∵CD⊥BD,AB∩BD=B, AB⊂平面ABD,BD⊂平面ABD, ∴CD⊥平面ABD.
............6分
(2)法一:由AB⊥平面BCD,得AB⊥BD,
∵AB=BD=1,∴S△ABD=.
∵M是AD的中点, ∴S△ABM=S△ABD=
由(1)知,CD⊥平面ABD,
∴三棱锥C-ABM的高h=CD=1,
因此三棱锥A-MBC的体积 VA-MBC=VC-ABM=S△ABM·h=.…………12分
法二:由AB⊥平面BCD知,平面ABD⊥平面BCD,又平面ABD∩平面BCD=BD,
如图,过点M作MN⊥BD交BD于点N,则MN⊥平面BCD,且MN=AB=,又CD⊥BD,BD=CD=1, ∴S△BCD=.
∴三棱锥A-MBC的体积VA-MBC=VA-BCD-VM-BCD=AB·S△BCD-MN·S△BCD=.
………………………12分
20(本小题满分12分)
解:以圆拱拱顶为坐标原点,以过拱顶的竖直直线为y轴,建立直角坐标系,设圆心为C,水面所在弦的端点为A、B,则由已知得A(6,-2).
设圆的半径为r,则C(0,-r),即圆的方程为
x2+(y+r)2=r2.①
将点A的坐标为(6,-2)代入方程①,解得r=10. ......6分
9
∴圆的方程为x2+(y+10)2=100.②
当水面下降1米后,可设点A′的坐标为(x0,-3)(x0>3),如
图所示,将A′的坐标(x0,-3)代入方程②,求得.
∴水面下降1米后,水面宽为……………12分
21,解:(1)在△PAD中,因为E,F分别为AP,AD的中点,∴EF∥PD.
∵EF不在平面PCD中,PD⊂平面PCD
∴直线EF∥平面PCD.--------------------(6分)
(2)连接BD.∵AB=AD,∠BAD=60°.
∴△ABD为正三角形
∵F是AD的中点,∴BF⊥AD.
∵平面PAD⊥平面ABCD,BF⊥平面ABCD,
平面PAD∩平面ABCD=AD,∴BF⊥平面PAD.
又因为BF⊂平面EBF,所以平面BEF⊥平面PAD -----------------(12分)
22(本小题满分12分)
解:(Ⅰ)由条件可知,设,则解得或,所以或………………4分
(Ⅱ)由条件可知圆心到直线的距离,设直线的方程为,
则,解得或
所以直线的方程为或………………8分
(III)设,过、、三点的圆即以为直径的圆,
其方程为
整理得与相减得
即
9
由得
所以两圆的公共弦过定点………………12分
9