福建省福州市2019—2020学年度第一学期高三期末质量检测文科数学试卷（附参考答案） 14页

数学试题（第 1 页 共 6 页） 准考证号 姓名 . （在此卷上答题无效） 绝密★启用前 2019—2020 学年度第一学期福州市高三期末质量检测 数学（文科）试题 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷 1 至 3 页，第Ⅱ卷 4 至 6 页．满分 150 分． 注意事项： 1. 答题前，考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名．考 生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、 姓名是否一致． 2. 第Ⅰ卷每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑．如需 改动，用橡皮擦干净后，再选涂其它答案标号．第Ⅱ卷用 0.5 毫米黑色签字笔在答 题卡上书写作答．在试题卷上作答，答案无效． 3. 考试结束，考生必须将试题卷和答题卡一并交回． 第 Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只 有一项是符合题目要求的． 1. 设复数  i2 iz ，则 z  A． 3 B． 5 C．3 D．5 2. 已知集合  |0 2Axx x ≤≥或 ，  |1 2Bx x≤≤ ，则 A． A B B． B A C． AB D． AB R 3. 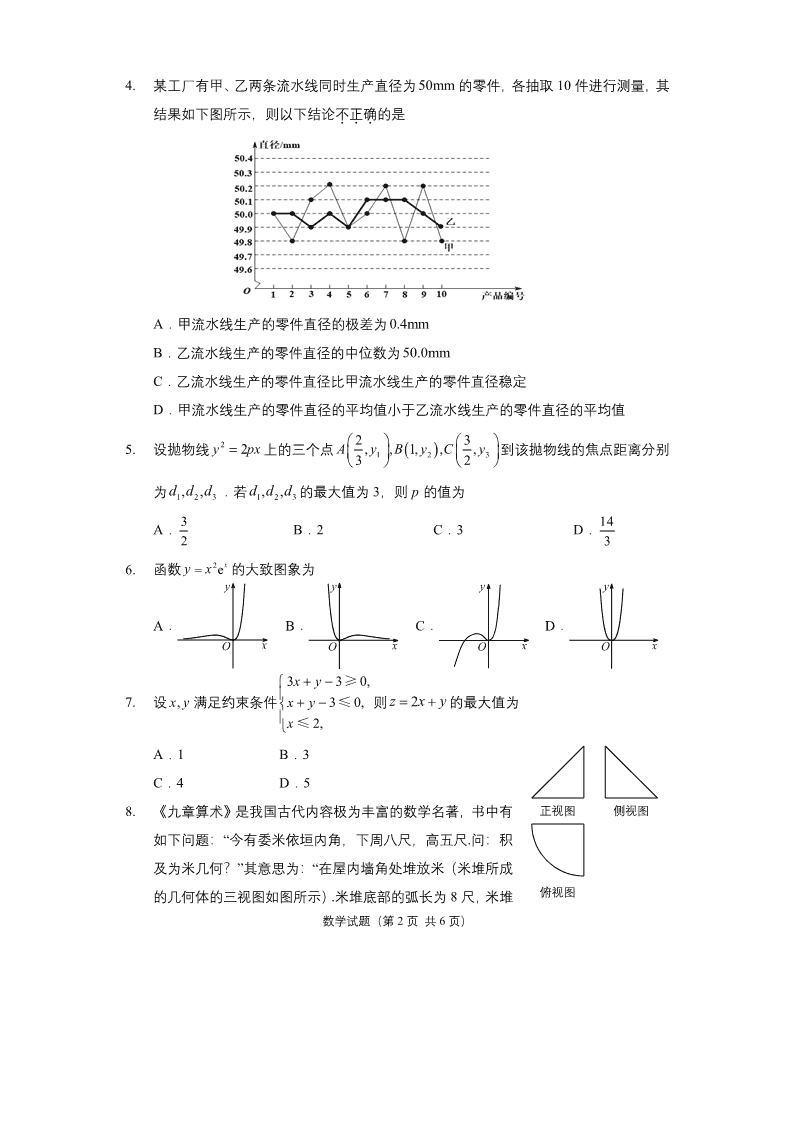执行如图所示的程序框图，若输入的 ,ab分别为 4,2，则输出的 n  A．2 B．3 C．4 D．5   数学试题（第 2 页 共 6 页） 4. 某工厂有甲、乙两条流水线同时生产直径为50mm 的零件，各抽取 10 件进行测量，其 结果如下图所示，则以下结论不正确．．．的是 A．甲流水线生产的零件直径的极差为 0.4mm B．乙流水线生产的零件直径的中位数为50.0mm C．乙流水线生产的零件直径比甲流水线生产的零件直径稳定 D．甲流水线生产的零件直径的平均值小于乙流水线生产的零件直径的平均值 5. 设抛物线 2 2ypx 上的三个点 12 3 23,,1,, ,32AyByCy     到该抛物线的焦点距离分别 为 123,,ddd．若 123,,ddd的最大值为 3，则 p 的值为 A． 3 2 B．2 C．3 D． 14 3 6. 函数 2exyx 的大致图象为 A． B． C． D． 7. 设 ,xy满足约束条件 330, 30, 2, xy xy x     ≥ ≤ ≤ 则 2zxy的最大值为 A．1 B．3 C．4 D．5 8. 《九章算术》是我国古代内容极为丰富的数学名著，书中有 如下问题：“今有委米依垣内角，下周八尺，高五尺.问：积 及为米几何？”其意思为：“在屋内墙角处堆放米（米堆所成 的几何体的三视图如图所示）.米堆底部的弧长为 8 尺，米堆 O x y O x y O x y O x y 正视图 侧视图 俯视图 数学试题（第 3 页 共 6 页） 的高为 5 尺，问米堆的体积和堆放的米各为多少?”已知 1 斛米的体积约为 1.6 立方尺， 圆周率 3 ，估算出堆放的米约有 A．20 斛 B．21 斛 C．22 斛 D．23 斛 9. 已知函数    sinfx x   的部分图象如图所示，则  f x 的单调递减区间为 A． π4π11π4π,,43123 kkk Z B． 13π 5ππ, π ,12 12kkk  Z C． π11π2π, 2π,412kkk Z D． 13π 3 π 5π 3 π,,12 4 12 4 kkk   Z 10. 若 2cos2 1 sin2x x ，则 tan x  A． 1 B． 1 3 C． 1 或 1 3 D． 1 或 1 3 或 3 11. 已知函数  ln afx x x  ，直线 3yx  与曲线  yfx 相切，则 a  A．1 B．2 C．3 D．4 12. 已知双曲线 22 22:1xyE ab（ 0, 0ab＞ ＞ ）的左、右焦点分别为 12,F F ，若 E 上点 A 满 足 122AFAF ，且 12F AF 的取值范围为 2π ,π3      ，则 E 的离心率的取值范围是 A． 3, 5 B． 7,3 C． 3, 5 D． 7,9 x y O 1 7π 12 5π 12 数学试题（第 4 页 共 6 页） 绝密★启用前 2019—2020 学年度第一学期福州市高三期末质量检测 数学（文科）试题 第Ⅱ卷 注意事项： 用 0.5 毫米黑色签字笔在答题卡上书写作答．在试题卷上作答，答案无效． 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分．把答案填在题中的横线上． 13. 已知向量 ,ab满足 3, 1ab， a 与 b 的夹角为30 ，则  ab ． 14. 已知函数  21,0, 2, 0. x xfx xx     ＞ ≤ 若    10fa f  ，则 a  ． 15. 在钝角 ABC△ 中，已知 7, 1AB AC，若 ABC△ 的面积为 6 2 ，则 BC 的长为 ． 16. 已知正方体 111 1ABCD A B C D 的棱长为 2，直线 1AC  平面 .平面 截此正方体所得 截面有如下四个结论： ①截面形状可能为正三角形； ②截面形状可能为正方形； ③截面形状不可能是正五边形； ④截面面积最大值为33． 其中所有正确结论的编号是 ． 三、解答题：本大题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17～21 题为必考题，每个试题考生都必须作答．第 22、23 题为选考题，考生根据要 求作答． （一）必考题：共 60 分． 17. （本小题满分 12 分） 垃圾分一分，城市美十分；垃圾分类，人人有责．某市为进一步推进生活垃圾分类工 作，调动全民参与的积极性，举办了“垃圾分类游戏挑战赛”．据统计，在为期 2 个月的活 动中，共有 640 万人次参与．为鼓励市民积极参与活动，市文明办随机抽取 200 名参与该 活动的网友，以他们单次游戏得分作为样本进行分析，由此得到如下频数分布表： 数学试题（第 5 页 共 6 页） 单次游戏得分 [30,40) [40,50) [50,60) [60,70) [70,80) [80,90] 频数 10 40 60 40 30 20 （1）根据数据，估计参与活动的网友单次游戏得分的平均值及标准差（同一组中的数 据用该组区间的中点值作代表）；（其中标准差的计算结果要求精确到 0.01） （2）若要从单次游戏得分在[30,40) 、[60,70) 、[80,90] 的三组参与者中，用分层抽样 的方法选取 7 人进行电话回访，再从这 7 人中任选 2 人赠送话费，求此 2 人单次游戏得分不 在同一组内的概率. 附： 185 1 03.6 ， 370 19.24 . 18. （本小题满分 12 分） 已知数列 na 的前 n 项和 2 nSnpn，且 248,,aaa成等比数列． （1）求数列 na 的通项公式； （2）设 1 4 n nn b aa   ，求数列 nb 的前 n 项和 nT ． 19. （本小题满分 12 分） 如图，在四棱锥 P ABCD 中，底面 ABCD 为正方形， PA  底面 ABCD ， PAAB ， E 为线段 PB 的中点， F 为线段 BC 上的动点. （1）平面 AEF 与平面 PBC 是否互相垂直？如果垂直， 请证明；如果不垂直，请说明理由． （2）若 3AB  ， F 为线段 BC 的三等分点，求多面体 PAEFCD 的体积． 20. （本小题满分 12 分） 已知圆 22: 4 3xyO ，椭 圆 22 22:1xyC ab  （ 0ab＞ ＞ ）的短轴长等于圆O半径的 6 倍， C 的离心率为 2 2 ． （1）求 C 的方程； （2）若直线l 与 C 交于 ,A B 两点，且与圆 O 相切，证明：OA OB ． P A B CD E F 数学试题（第 6 页 共 6 页） 21. （本小题满分 12 分） 已知函数   cos 1f xaxx  在 π0, 6      上的最大值为 3π 16  ． （1）求 a 的值； （2）证明：函数 f x 在区间 π0, 2   上有且仅有 2 个零点． （二）选考题：共 10 分．请考生在第 22，23 两题中任选一题作答．如果多做，则按所做 第一个题目计分，作答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑． 22.（本小题满分 10 分）选修 44 ：坐标系与参数方程 在直角坐标系 xOy 中，直线 l 的参数方程为 35,2 13 2 x t y t     （t 为参数）．以坐标原点为 极点，x 轴的正半轴为极轴建立极坐标系，曲线 C 的极坐标方程为 2cos  ． （1）求 C 的直角坐标方程； （2）设 点 M 的直角坐标为 5, 3 ， l与曲线 C 的交点为 ,A B ，求 11 MAMB 的值． 23.（本小题满分 10 分）选修 45 ：不等式选讲 已知函数 1() 2 1 2fx x x  的最小值为 m ． （1）求 m 的值； （2）若 ,,abc为正实数，且 abcm  ，证明： 2221 3abc≥ ． 文科数学参考答案及评分细则（第 1 页 共 8 页） 2019—2020 学年度第一学期福州市高三期末质量检测 数学（文科）参考答案及评分细则 评分说明： 1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题 的主要考查内容比照评分标准制定相应的评分细则。 2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的 内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数 的一半；如果后继部分的解答有较严重的错误，就不再给分。 3．解答右端所注分数，表示考生正确做到这一步应得的累加分数。 4．只给整数分数。选择题和填空题不给中间分。 一、选择题：本大题考查基础知识和基本运算．每小题 5 分，满分 60 分． 1．B 2．D 3．C 4．D 5．C 6．A 7．D 8．C 9．A 10．C 11．B 12．B 二、填空题：本大题考查基础知识和基本运算．每小题 5 分，满分 20 分． 13． 3 2 14． 5 15． 10 16．①③④ 三、解答题：本大题共 6 小题，共 70 分．解答应写出文字说明，证明过程或演算步骤． 17．本题主要考查用样本估计总体、平均数、标准差、古典概型等基础知识，考查考生 运用概率与统计知识解决实际问题的能力、数据处理能力，考查的核心素养主要有 数学建模、数学抽象、数学运算、数据分析．满分 12 分． 【解答】（1）参与该活动的网友单次游戏得分的平均值 1 35 10 45 40 55 60 65 40 75 30 85 20200x    ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 2 分 60 ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 3 分 标准差 22222 225 10 15 40 5 60 5 40 15 30 25 20 200s     ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 5 分 185 13.60． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 6 分 （2）用分层抽样抽取 7 人，其中得分在[30,40) 的有1人，得分在[60,70) 的有 4 人，得 分在[80,90] 的有 2 人， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 7 分 文科数学参考答案及评分细则（第 2 页 共 8 页） 分别记为 a , 1234,,,bbbb, 12,cc， 7 人中任选 2 人，有 21 种结果， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 8 分 其中 2 人得分在同一组的有 7 种，分别是 12,bb 、 13,bb 、 14,bb 、 23,bb 、 24,bb 、  34,bb 、 12,cc ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 10 分 故 2 人得分不在同一组内的概率 721 21 3P  .ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 12 分 18．本小题考查数列的通项与前 n 项和的关系、等比数列、裂项相消法求数列的和等基础 知识，考查运算求解能力，考查函数与方程思想、化归和转化思想等，考查的核心 素养主要有逻辑推理、数学运算等．满分 12 分． 【解答】（1）当 1n  时, 111aS p， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 1 分 当 2n≥ 时， 22 1 [( 1) ( 1)] 2 1nnnaSS npnn pn n p   ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 3 分 经检验， 1n  时也满足上式，所以 21nan p  ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 4 分 因为 248,,aaa成等比数列， 所以 2 28 4aa a ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 5 分 即     23157pp p，解得 1p  ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 6 分 所以 2.nan ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 7 分 （2）由（1）及题设得， 1 4111 (1) 1n nn b aa nn n n  ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 9 分 所以 12nnTbb b 111 11(1 ) ( ) ( )223 1nn    ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 11 分 11 1n  = 1 n n  ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 12 分 19．本小题主要考查空间直线与直线、直线与平面、平面与平面的位置关系、空间几何 体的体积等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查化 归与转化思想等，考查的数学素养主要有逻辑推理、直观想象等．满分 12 分． 【解答】解法一：（1）平面 AEF 与平面 PBC 互相垂直， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 1 分 理由如下： 文科数学参考答案及评分细则（第 3 页 共 8 页） 因为 PA  底面 ABCD ， BC  平面 ABCD ， 所以 PA BC ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 2 分 因为 ABCD 为正方形，所以 ABBC 又 PAABA ，且 ,PAAB 平面 PAB ， 所以 BC  平面 PAB ． 因为 AE  平面 PAB ，所以 AEBC ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 3 分 因为 PAAB ， E 为线段 PB 的中点，所以 AEPB ， 又 PBBCB ，且 ,PBBC 平面 PBC ， 所以 AE  平面 PBC ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 4 分 因为 AE  平面 AEF ，所以平面 AEF  平面 PBC ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 6 分 （2）因为 PA  底面 ABCD ， E 为线段 PB 的中点， 所以点 E 到底面 ABCD 的距离为 1 2 PA  3 2 ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 7 分 则 1 333 93PABCDV    ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 8 分 又 F 为线段 BC 的三等分点， 当 1 13BF BC时， 11 333132 24E ABFV    ， 所以多面体 PAEFCD 的体积为 3339 44P ABCD E ABFVV； ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 10 分 当 2 23BF BC时， 11 333232 22EABFV     ， 所以多面体 PAEFCD 的体积为 3159 22P ABCD E ABFVV   ．ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 11 分 综上，多面体 PAEFCD 的体积为 33 4 或 15 2 . ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 12 分 解法二：（1）平面 AEF 与平面 PBC 互相垂直， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 1 分 理由如下： 因为 PA  底面 ABCD ， PA  平面 PAB ，所以平面 PAB  底面 ABCD ，ꞏꞏꞏꞏꞏꞏꞏꞏꞏ 2 分 又平面 PAB 底面 ABCD AB ， BCAB ， BC  平面 ABCD ， 所以 BC  平面 PAB ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 3 分 P A B CD E F 文科数学参考答案及评分细则（第 4 页 共 8 页） 因为 AE  平面 PAB ，所以 AEBC ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 3 分 因为 PAAB ， E 为线段 PB 的中点，所以 AEPB ， 又 PBBCB ，且 ,PBBC 平面 PBC ， 所以 AE  平面 PBC ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 4 分 因为 AE  平面 AEF ， 所以平面 AEF  平面 PBC . ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 6 分 （2）同解法一． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 12 分 20．本小题考查圆与椭圆的标准方程及其几何性质、直线与圆的位置关系、直线椭圆的 位置关系等基础知识，考查推理论证能力、运算求解能力，考查数形结合思想、化 归与转化的思想、分类与整合思想等，考查的数学素养主要有逻辑推理、直观想 象、数学运算等．满分 12 分． 【解答】解法一：（1）依题意，圆O半径等于 23 3 ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 1 分 因为椭圆的短轴长等于圆O半径的 6 倍， 所以 2326 223b   ，解得 2b  ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 2 分 因为 C 的离心率为 2 2 ，所以 2 2 c a  ， ① ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 3 分 又因为 22 2acb，所以 222ac， ② 联立①② ，解得 2 4a  ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 4 分 所以 C 的方程为 22 142 xy. ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 5 分 （2）证明：①当直线l 斜率不存在时, 直线l 的方程为 23 3x  ，或 23 3x  ． 当 23 3x  时， 2323 23 23(,),(, )33 3 3AB ，则 44033OA OB   ，故 OA OB ． 同理可证，当 23 3x  时， OA OB ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 6 分 ②当直线l 斜率存在时，设其方程为 11 2 2,(, ),(, ),ykxmAxyBxy 因为直线l 与圆相切，所以 2 23 | | 3 1 m k   ，即 223440mk , ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 7 分 文科数学参考答案及评分细则（第 5 页 共 8 页） 由 22 , 142 ykxm xy   得， 22 2(1 2 ) 4 2 4 0kx kmxm, ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 8 分 所以     22 2 2 2 216 8 1 2 2 8 4 2 0km k m k m       ＞ ，且 12 2 2 12 2 4 ,12 24,12 kmxx k mxx k      ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 9 分 所以 12 1 2()()OA OB x x kx m kx m      22 12 1 2(1 ) ( )kxxkmxx m    ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 10 分 22 222 2 2 (1 )(2 4) 4 (1 2 ) 12 km kmm k k   22 2 34 4 12 km k   0 ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 11 分 所以 .OA OB 综上， .OA OB ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 12 分 解法二：（1）同解法一． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 5 分 （2）①当直线方程为 23 3y  时, 2323 2323(,),(,)33 33AB ，则 44033OA OB  ，故 .OA OB 同理可证，当直线方程为 23 3y  时， .OA OB ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 6 分 ②当直线l 不与 x 轴平行时,设其方程为 11 2 2,(, ),(, ),x ty m A x y B x y 因为直线l 与圆相切，所以 2 23 | | 3 1 m t   ，即 223440.mt  ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 7 分 由 22 , 142 x ty m xy   得， 22 2(2)2 40.tytmym ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 8 分 文科数学参考答案及评分细则（第 6 页 共 8 页） 所以     22 2 2 2 244248240tm t m t m       ＞ ，且 12 2 2 12 2 2 ,2 4.2 tmyy t myy t       ꞏꞏꞏꞏ 9 分 12 1 2()()OA OB y y ty m ty m    22 12 1 2(1 ) ( )tyytmyy m    ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 10 分 2 2 22 22 2 (1 )( 4) 2 ( 2) 2 tm tmmt t   22 2 344 2 mt t    0 ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 11 分 所以，OA OB ． 综上， .OA OB ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 12 分 21．本小题主要考查导数及其应用、函数的零点、函数的最值与值域等基础知识，考查 推理论证能力、运算求解能力、抽象概括能力等，考查函数与方程思想、化归与转 化思想、分类与整合思想、数形结合思想等，考查的数学素养主要有逻辑推理、直 观想象、数学运算等．满分 12 分． 【解答】（1）   xxxaxf sincos/  ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 1 分 因为     6,0 x ，所以 cos sin 0xx＞≥，又10x＞≥， 所以1cos sinx xx ＞ ，即 0sincos  xxx ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 2 分 当 0a 时，   0/ xf ，所以  f x 在区间 π0, 6      上递增， 所以  16 312 3 66max       afxf ，解得 2a ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 3 分 当 0a 时，   0/ xf ，所以  f x 在区间 π0, 6      上递减， 所以   10max  fxf ，不合题意． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 4 分 当 0a  ，   1fx ，不合题意． 综上， 2a . ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 5 分 （2）设  xxxxg sincos  ， 文科数学参考答案及评分细则（第 7 页 共 8 页） 则        200cossin2/ xxxxxg ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 6 分 所以 xg 在      2,0  上单调递减，又  022,010      gg ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 7 分 所以存在唯一的      2,00 x ，使得   00 xg ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 8 分 当 00 xx  时，  0xg ，即     02/  xgxf ，所以    0,0 xxf 在 上单调递增；当 20  xx 时，  0xg ，即     02/  xgxf ，所以    0,0 xxf 在 上单调递减， ꞏꞏ 9 分 又  012,014 2 4,010           fff ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 10 分 所以 f x 在 π0, 4   与 ππ,42   上各有一个零点， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 11 分 综上，函数  xf 在区间      2,0  上有且仅有两个零点. ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 12 分 （二）选考题：共 10 分．请考生在第 22，23 两题中任选一题作答．如果多做，则按所做 第一个题目计分，作答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑． 22．本题考查极坐标方程和直角坐标方程的互化，直线和圆的位置关系，以及直线的参 数方程的参数的几何意义等基础知识,考查学生的逻辑推理能力,化归与转化能力．考 查的核心素养是直观想象、逻辑推理与数学运算. 【解答】（1）由 2cos  ，得 2 2cos  ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 2 分 将 cos , sin x y        代入得， 222x yx， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 4 分 所以 C 的直角坐标方程为 22(1) 1xy． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 5 分 （2）设 ,AB所对应的参数分别为 12,tt， 因为直线 l 的参数方程为 35,2 ( 13 2 x t t yt     为参数ሻ，所以 M (5, 3) 在 l 上, ꞏꞏꞏꞏꞏꞏꞏꞏꞏ 6 分 把 l 的参数方程代入 22(1) 1xy可得 2 53 180,tt  ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 7 分 所以 2(53)41830     ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 8 分 文科数学参考答案及评分细则（第 8 页 共 8 页） 所以 12 1253, 180tt tt ＞ ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 9 分 故 11 MAMB = 12 12 12 12 |||| | ||||| 53 ||||||||||18 tt ttMA MB MA MB t t t t   . ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 10 分 23．本题考查含有绝对值的函数的最值，基本不等式的应用等基础知识,考查学生的逻辑 推理能力,化归与转化能力.考查的核心素养是直观想象、逻辑推理与数学运算. 【解答】（1）根据题意,函数 113, ,1 22() |2 1| 312 ,,22 xx fx x x xx     ≥ ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 2 分 所以 ()f x 为在 1, 2   单调递减，在 1 ,2    单调递增， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 3 分 所以 min 1() 1, 1.2fx f m 即 ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 5 分 （2）由(1)知， 1m  ，所以 1,abc  ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 6 分 又因为 ,,abc为正实数， 222ab ab ≥ ， 222bc bc ≥ ， 222ac ac ≥ ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 8 分 所以 22222a b c ab bc ac ≥ ，即 222a b c ab bc ac ≥ ， ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 9 分 所以 22221( ) 2 2 2a b c a b c ab bc ca   2223( )abc≤ ， 即 2221 3abc≥ ． ꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏꞏ 10 分