- 274.22 KB
- 2021-05-31 发布
2016-2017学年广东省广州市越秀区培正中学高二(上)摸底数学试卷
一、选择题(共12小题)
1.设集合M={﹣1,0,1},N={x|x2=﹣x},则M∩N=( )
A.{0} B.{1,0} C.(﹣1,0) D.{﹣1,0}
2.直线l过点(1,﹣2),且与直线2x+3y﹣1=0垂直,则l的方程是( )
A.2x+3y+4=0 B.2x+3y﹣8=0 C.3x﹣2y﹣7=0 D.3x﹣2y﹣1=0
3.函数f(x)=()x﹣x+2的零点所在的一个区间是( )
A.(﹣1,0) B.(0,1) C.(1,2) D.(2,3)
4.若||=1,||=,且⊥(﹣),则向量,的夹角为( )
A.45° B.60° C.120° D.135°
5.实数a=0.2,b=log0.2,c=的大小关系正确的是( )
A.a<c<b B.a<b<c C.b<a<c D.b<c<a
6.设x,y满足约束条件,则z=x﹣y的最大值为( )
A.﹣5 B.﹣1 C.5 D.1
7.已知函数f(x)=sin(2x+),则下列结论中正确的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)的图象关于点(,0)对称
C.由函数f(x)的图象向右平移个单位长度可以得到函数y=sin2x的图象
D.函数f(x)在区间(,)上单调递增
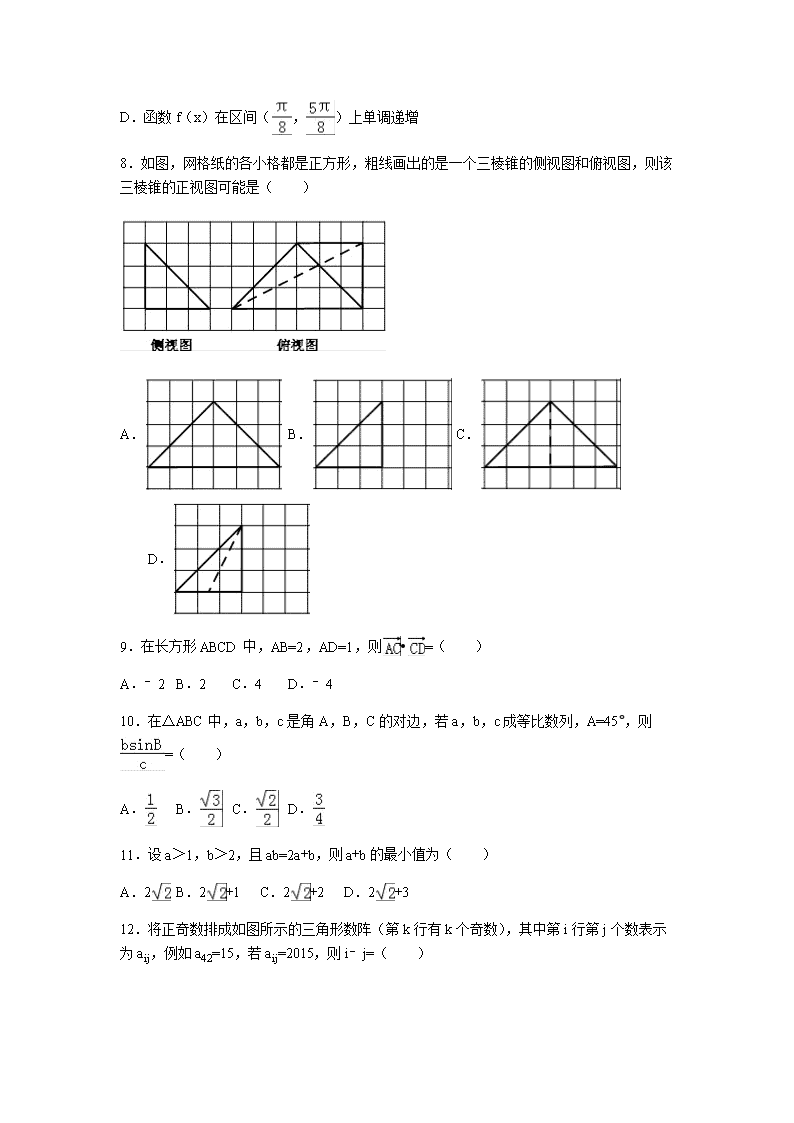
8.如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )
A. B. C. D.
9.在长方形ABCD中,AB=2,AD=1,则•=( )
A.﹣2 B.2 C.4 D.﹣4
10.在△ABC中,a,b,c是角A,B,C的对边,若a,b,c成等比数列,A=45°,则=( )
A. B. C. D.
11.设a>1,b>2,且ab=2a+b,则a+b的最小值为( )
A.2 B.2+1 C.2+2 D.2+3
12.将正奇数排成如图所示的三角形数阵(第k行有k个奇数),其中第i行第j个数表示为aij,例如a42=15,若aij=2015,则i﹣j=( )
A.26 B.27 C.28 D.29
二.填空题
13.已知等差数列{an},a4+a6=10,前5项的和S5=5,则其公差为 .
14.集合M={x|lg(1﹣x)<0},集合N={x|﹣1≤x≤1},则M∩N= .
15.已知平面向量与的夹角为, =(1,),|﹣2|=2.则||= .
16.已知函数y=a1﹣x(a>0且a≠1)的图象恒过点A.若点A在直线mx+ny﹣1=0(mn>0)上,则的最小值为 .
三、解答题
17.已知数列{an}的前n项和为Sn,且Sn=n2+n(n∈N*)
(1)求数列{an}的通项公式an.
(2)若数列{bn}满足bn=(n∈N*),Tn是数列{bn}的前n项和,求T9.
18.在△ABC中,a,b,c分别为内角A,B,C的对边,2bsinB=(2a+c)sinA+(2c+a)sinC.
(Ⅰ) 求B的大小;
(Ⅱ) 若b=,A=,求△ABC的面积.
19.已知直线l:y=kx与圆C1:(x﹣1)2+y2=1相交于A、B两点,圆C2与圆C1相外切,且与直线l相切于点M(3,),求
(1)k的值
(2)|AB|的值
(3)圆C2的方程.
2016-2017学年广东省广州市越秀区培正中学高二(上)摸底数学试卷
参考答案与试题解析
一、选择题(共12小题)
1.设集合M={﹣1,0,1},N={x|x2=﹣x},则M∩N=( )
A.{0} B.{1,0} C.(﹣1,0) D.{﹣1,0}
【考点】交集及其运算.
【分析】求出N中方程的解确定出N,找出M与N的交集即可.
【解答】解:由N中方程整理得:x(x+1)=0,
解得:x=0或x=﹣1,即N={﹣1,0},
∵M={﹣1,0,1},
∴M∩N={﹣1,0},
故选:D.
2.直线l过点(1,﹣2),且与直线2x+3y﹣1=0垂直,则l的方程是( )
A.2x+3y+4=0 B.2x+3y﹣8=0 C.3x﹣2y﹣7=0 D.3x﹣2y﹣1=0
【考点】直线的一般式方程与直线的垂直关系.
【分析】由条件利用两条直线垂直的性质求得要求直线的斜率,再用点斜式求得要求直线的方程.
【解答】解:由题意可得,要求直线的斜率为,再根据所求直线过点(1,﹣2),可得它的方程为y+2=(x﹣1),
即3x﹣2y﹣7=0,
故选C.
3.函数f(x)=()x﹣x+2的零点所在的一个区间是( )
A.(﹣1,0) B.(0,1) C.(1,2) D.(2,3)
【考点】函数零点的判定定理.
【分析】判断函数值,利用零点定理推出结果即可.
【解答】解:函数,
可得:f(﹣1)=5>0,
f(0)=3>0,
f(1)=>0,
f(2)=>0,
f(3)=﹣0,
由零点定理可知,函数的零点在(2,3)内.
故选:D.
4.若||=1,||=,且⊥(﹣),则向量,的夹角为( )
A.45° B.60° C.120° D.135°
【考点】数量积表示两个向量的夹角.
【分析】设向量的夹角为θ,由=0,可得=1,再利用两个向量的夹角公式求出cosθ,进而求得θ 的值.
【解答】解:设向量的夹角为θ,由题意可得==0,可得
=1,即 = cosθ=1×cosθ,
解得 cosθ=.
再由 0≤θ≤π可得θ=,
故选A.
5.实数a=0.2,b=log0.2,c=的大小关系正确的是( )
A.a<c<b B.a<b<c C.b<a<c D.b<c<a
【考点】对数函数的图象与性质;指数函数的图象与性质;不等关系与不等式.
【分析】根据指数函数,对数函数和幂函数的性质分别判断a,b,c的大小,即可判断.
【解答】解:根据指数函数和对数函数的性质,知log0.2<0,0<0.2<1,,
即0<a<1,b<0,c>1,
∴b<a<c.
故选:C.
6.设x,y满足约束条件,则z=x﹣y的最大值为( )
A.﹣5 B.﹣1 C.5 D.1
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
【解答】解:作出不等式组对应的平面区域如图:
由z=x﹣y,得y=x﹣z表示,斜率为1纵截距为﹣z的一组平行直线,
平移直线y=x﹣z,当直线经过点A时,直线y=x﹣z截距最小,z最大.
由解得A(﹣1,﹣2)时,此时zmax=﹣1+2=1.
故选:D.
7.已知函数f(x)=sin(2x+),则下列结论中正确的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)的图象关于点(,0)对称
C.由函数f(x)的图象向右平移个单位长度可以得到函数y=sin2x的图象
D.函数f(x)在区间(,)上单调递增
【考点】正弦函数的单调性;三角函数的周期性及其求法;函数y=Asin(ωx+φ)的图象变换.
【分析】由条件利用正弦函数的周期性、图象的对称性、单调性以及y=Asin(ωx+φ)的图象变换规律,得出结论.
【解答】解:对于函数f(x)=sin(2x+),它的最小正周期为=π,故排除A;
令x=,求得f(x)=,故函数f(x)的图象不关于点(,0)对称;故排除B;
把函数f(x)=sin(2x+)的图象向右平移个单位长度,
可以得到函数y=sin2(x﹣)+]=sin2x的图象,故C满足条件;
在区间(,)上,2x+∈(,),函数f(x)单调递减,故排除D,
故选:C.
8.如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )
A. B. C. D.
【考点】简单空间图形的三视图.
【分析】由已知中锥体的侧视图和俯视图,画出该几何的直观图,进而可得该锥体的正视图.
【解答】解:由已知中锥体的侧视图和俯视图,
可得该几何体是三棱锥,
由侧视图和俯视图可得,该几何的直观图如图P﹣ABC所示:
顶点P在以BA和BC为邻边的平行四边形ABCD上的射影为CD的中点O,
故该锥体的正视图是:
故选A
9.在长方形ABCD中,AB=2,AD=1,则•=( )
A.﹣2 B.2 C.4 D.﹣4
【考点】平面向量数量积的运算.
【分析】利用向量的垂直与数量积的关系、向量的三角形法则、数量积运算即可得出.
【解答】解:∵,∴=0.
∵,,
∴•=
=﹣0
=﹣22=﹣4.
故选:D.
10.在△ABC中,a,b,c是角A,B,C的对边,若a,b,c成等比数列,A=45°,则=( )
A. B. C. D.
【考点】等比数列的性质;正弦定理.
【分析】由a,b,c成等比数列,根据等比数列的性质化简得到关于a,b及c的关系式,利用正弦定理化简后得到关于sinA,sinB及sinC的关系式,然后把所求的式子也利用正弦定理化为关于正弦函数的式子,把化简得到关系式及A的度数代入求出值.
【解答】解:由a,b,c成等比数列,得到b2=ac,由正弦定理得:sin2B=sinA•sinC.
又A=45°,
∴===sinA=.
故选:C.
11.设a>1,b>2,且ab=2a+b,则a+b的最小值为( )
A.2 B.2+1 C.2+2 D.2+3
【考点】基本不等式.
【分析】由已知式子可得b=,代入整理可得a+b=a﹣1++3,由基本不等式可得.
【解答】解:∵a>1,b>2,且ab=2a+b,
∴ab﹣b=2a,∴b(a﹣1)=2a,解得b=,
∴a+b=a+==
==a﹣1++3
≥3+2=3+2
当且仅当a﹣1=即a=1+时取等号
故选:D
12.将正奇数排成如图所示的三角形数阵(第k行有k个奇数),其中第i行第j个数表示为aij,例如a42=15,若aij=2015,则i﹣j=( )
A.26 B.27 C.28 D.29
【考点】归纳推理.
【分析】分析正奇数排列的正三角图表知,第i行(其中i∈N*)有i个奇数,且从左到右按从小到大的顺序排列,则2015是第1008个奇数,由等差数列的知识可得,它排在第几行第几个数
【解答】解:根据正奇数排列的正三角图表知,2015是第1008个奇数,应排在i行(其中i∈N*),
则1+2+3+…+(i﹣1)=i(i﹣1)≤1008①,
且1+2+3+…+i=i(i+1)>1008②;
验证i=45时,①②式成立,所以i=45;
第45行第1个奇数是2××44×45+1=1981,
而1981+2(j﹣1)=2015,
∴j=18;
∴i﹣j=45﹣18=27.
故选:B
二.填空题
13.已知等差数列{an},a4+a6=10,前5项的和S5=5,则其公差为 2 .
【考点】等差数列的前n项和;等差数列的通项公式.
【分析】设公差为d,由题意可得 2a1+8d=10,5a1+=5,解方程组求得d的值.
【解答】解:∵等差数列{an},a4+a6=10,前5项的和S5=5,设公差为d.
由题意可得 2a1+8d=10,5a1+=5,
解方程组求得d=2,
故答案为 2.
14.集合M={x|lg(1﹣x)<0},集合N={x|﹣1≤x≤1},则M∩N= (0,1) .
【考点】交集及其运算.
【分析】分别求出关于集合A、B中x的范围,从而求出其交集即可.
【解答】解:∵M={x|lg(1﹣x)<0}={x|0<x<1},
N={x|﹣1≤x≤1},
∴M∩N=(0,1),
故答案为:(0,1).
15.已知平面向量与的夹角为, =(1,),|﹣2|=2.则||= 2 .
【考点】平面向量数量积的运算.
【分析】对|﹣2|=2两边平方得出关于||的方程,即可解出.
【解答】解:||=2, =||||cos=||,
∵|﹣2|=2,∴()2=,
即4||2﹣4||+4=12,解得||=2.
故答案为:2.
16.已知函数y=a1﹣x(a>0且a≠1)的图象恒过点A.若点A在直线mx+ny﹣1=0(mn>0)上,则的最小值为 3+2 .
【考点】基本不等式.
【分析】根据题意,求出点A的坐标,得出m+n=1且m>0,n>0,利用基本不等式求的最小值即可.
【解答】解:函数y=a1﹣x(a>0且a≠1)的图象恒过点A,
即1﹣x=0时,y=a0=1,∴A(1,1);
又点A在直线mx+ny﹣1=0(mn>0)上,
∴m+n﹣1=0,即m+n=1;
又∵mn>0,∴m>0,n>0,
∴=+
=3++≥3+2=3+2,
当且仅当=,即n=m=﹣1时“=”成立;
∴的最小值为3+2.
故答案为:.
三、解答题
17.已知数列{an}的前n项和为Sn,且Sn=n2+n(n∈N*)
(1)求数列{an}的通项公式an.
(2)若数列{bn}满足bn=(n∈N*),Tn是数列{bn}的前n项和,求T9.
【考点】数列的求和;数列递推式.
【分析】(1)利用n=1时,a1=S1;n≥2时,an=Sn﹣Sn﹣1,即可得出.
(2)==(﹣),利用“裂项求和”即可得出.
【解答】解:(1)∵数列{an}的前n项和为Sn,且Sn=n2+n,
∴n=1时,a1=2;
n≥2时,an=Sn﹣Sn﹣1=2n,
当n=1时,上式也成立.
∴an=2n(n∈N*).
(2)==(﹣),
T9= [(1﹣)+(﹣)+…+(﹣)]=×(1﹣)=.
18.在△ABC中,a,b,c分别为内角A,B,C的对边,2bsinB=(2a+c)sinA+(2c+a)sinC.
(Ⅰ) 求B的大小;
(Ⅱ) 若b=,A=,求△ABC的面积.
【考点】正弦定理的应用.
【分析】(Ⅰ)由正弦定理,化简整理a2+c2﹣b2+ac=0,再由余弦定理,求得角B的大小,
(Ⅱ)由三角行的内角和定理,求得C及sinC,再由正弦定理,求得c的值,可求得三角形的面积.
【解答】(Ⅰ)解:∵2bsinB=(2a+c)sinA+(2c+a)sinC,
由正弦定理得,2b2=(2a+c)a+(2c+a)c,…
化简得,a2+c2﹣b2+ac=0.…
∴.…
∵0<B<π,
∴B=.…
(Ⅱ)解:∵A=,∴C=.…
∴sinC=sin==.…
由正弦定理得,,…
∵,B=,
∴.…
∴△ABC的面积=.…
19.已知直线l:y=kx与圆C1:(x﹣1)2+y2=1相交于A、B两点,圆C2与圆C1相外切,且与直线l相切于点M(3,),求
(1)k的值
(2)|AB|的值
(3)圆C2的方程.
【考点】直线和圆的方程的应用.
【分析】(1)点M在直线上,即可求出k的值;
(2)求出圆心到直线有距离,即可求出|AB|;
(3)利用圆C1与圆C2相切,可得,分类讨论,即可求出圆C2的方程.
【解答】解:(1)由题意知,点M在直线上,所以
(2)圆心到直线有距离,于是
(3)设所求的圆心的坐标为C2(m,n),半径为R.
由题意知,即,从而R=C2M=2|m﹣3|,
又圆C1与圆C2相切,则,
即:
(A)当m≥3时解得:m=4,n=0,R=2,则圆C2的方程为:(x﹣4)2+y2=4
(B)当m,3时解得:,则圆C2的方程为:
所以所求圆的方程为:(x﹣4)2+y2=4,
2016年10月30日