- 768.74 KB
- 2021-02-26 发布
江苏省江浦高级中学高三年级十月月考
数学试题 2020.10
一、 单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四
个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1、设集合,,则 ( )
A. B.
C. D. 或
2、已知,则= ( )
A. B. C. D.
3、已知向量,,若,则与夹角为 ( )
A. B. C. D.
4、函数的部分图象大致是 ( )
A. B.
C. D.
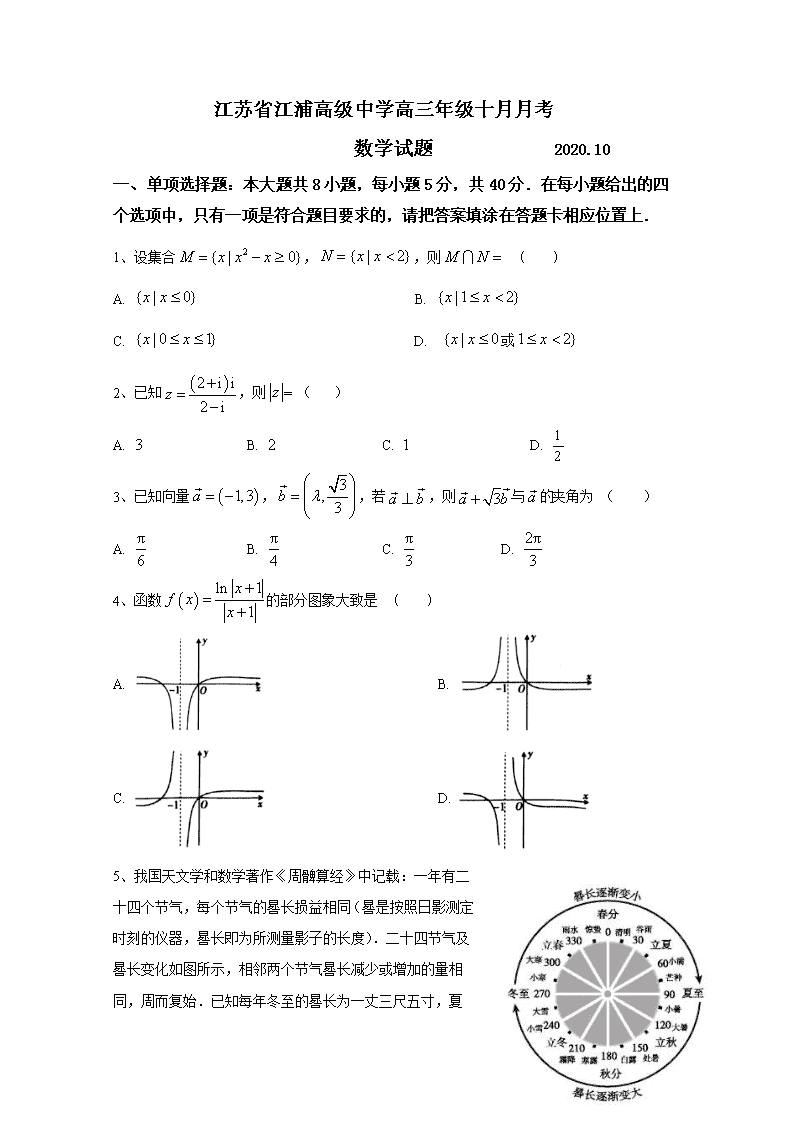
5、我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷
长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是 ( )
A. 相邻两个节气晷长减少或增加的量为一尺 B. 春分和秋分两个节气的晷长相同
C. 立冬的晷长为一丈五寸 D. 立春的晷长比立秋的晷长短
6、在△ABC中,如果,那么△ABC的形状为 ( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 等腰三角形
7、已知函数定义域为,且满足下列三个条件:① 任意,都有;② ;③ 为偶函数,则 ( )
A. B.
C. D.
8、直线是曲线和曲线的公切线,则
( )
A.2 B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四
个选项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上.全部选
对得5分,部分选对得3分,不选或有错选的得0分.
9、将函数的图象向右平移个单位长度得到函数的图象,若函数在区间上是单调增函数,则实数可能的取值为( )
A. B. 1 C. D. 2
10、关于双曲线与双曲线,下列说法正确的是( ).
A. 它们有相同的渐近线 B. 它们有相同的顶点
C. 它们的离心率不相等 D. 它们的焦距相等
11、台球运动已有五、六百年的历史,参与者用球杆在台上击球.若和光线一样,台球在球台上碰到障碍物后也遵从反射定律如图,有一张长方形球台ABCD,,现从角落A沿角的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则的值为( )
A. B. C. 1 D.
12、如图,在棱长为1的正方体中,P为线段上的动点,下列说法正确的是( )
A.对任意点P,平面 B.三棱锥的体积为
C. 存在点P,使得DP与平面所成角大小为 D. 线段DP长度的最小值为
三、填空题:本大题共4小题,每小题5分,共20分.请把答案填写在答题卡相应位置上.
13、已知,则=________.
14、的展开式中的系数为________.
15、若a,b均为非负数且a+b=1,,则的最小值为________.
16、在△ABC中,AB=3,AC=2,D为边BC上一点.若·=5,·=-,则·的值为________.
四、解答题:本大题共6小题,共70分.请在答题卡指定区域内作答,解答时
应写出必要的文字说明,证明过程或演算步骤.
17、(10分)△ABC的内角A,B,C的对边分别为a,b,c,设.
(1)求A;
(2)若,求sinC
18、(12分)从条件①,②,③,
中任选一个,补充到下面问题中,并给出解答.
已知数列的前项和为,,________.若,,成等比数列,求的值.
19、(12分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且正方形ABCD边长为2,PA⊥平面ABCD,PA=AB,E为线段PB的中点,F为线段BC上的动点.
(1)求证:AE⊥平面PBC;
(2)试确定点F的位置,使平面AEF与平面PCD所成的锐二面角为30°.
20、(12分)携号转网,也称作号码携带、移机不改号,即无需改变自己手机号码,就能转换运营商,并享受其提供的各种服务.2019年11月27日,工信部宣布携号转网在全国范围正式启动.某运营商为提质量保客户,从运营系统中选出300名客户,对业务水平和服务水平的评价进行统计,其中业务水平的满意率为,服务水平的满意率为,对业务水平和服务水平都满意的客户有180人.
(Ⅰ)完成下面列联表,并分析是否有的把握认为业务水平与服务水平有关;
对服务水平满意人数
对服务水平不满意人数
合计
对业务水平满意人数
对业务水平不满意人数
合计
(Ⅱ)为进一步提高服务质量,在选出的对服务水平不满意的客户中,抽取2名征求改进意见,用表示对业务水平不满意的人数,求的分布列与期望;
(Ⅲ)若用频率代替概率,假定在业务服务协议终止时,对业务水平和服务水平两项都满意的客户流失率为,只对其中一项不满意的客户流失率为,对两项都不满意的客户流
失率为,从该运营系统中任选4名客户,则在业务服务协议终止时至少有2名客户流失的概率为多少?
附:,.
0.10
0.05
0.025
0010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
21、(12分)已知椭圆:的离心率为,其左、右焦点分别为,,点为坐标平面内的一点,且,,为坐标原点.
(1)求椭圆的方程;
(2)设为椭圆的左顶点,,是椭圆上两个不同的点,直线,的倾斜角分别为,,且.证明:直线恒过定点,并求出该定点的坐标,
22、(12分)已知函数,.
(1)求函数的极值;
(2)若不等式对恒成立,求的取值范围
江苏省江浦高级中学高三年级十月月考
数学试题答案 2020.10
一、 单项选择题
1、D 2、C 3、B 4、A 5、D 6、A 7、B 8、C
二、多项选择题
9、ABC 10、CD 11、AD 12、ABD
三、填空题
13、 14、 15、 16、—3
四、解答题
17、解:(1)
即:
由正弦定理可得: 2分
4分
(2),由正弦定理得: 5分
又,
整理可得: 7分
解得:或 9分
因为所以,故.
10分
(2)法二:,由正弦定理得: 5分
又,
整理可得:, 7分
即
9分
由,所以
. 10分
18、解:若选择①,
因为,,所以,,
两式相减得,整理得.
即,. 4分
所以为常数列.,所以. 8分
(或由,利用相乘相消法,求得)
所以,,
又,,成等比数列,所以, 10分
所以,解得或(舍),
所以. 12分
若选择②,
由变形得,, 2分
所以,
易知,所以, 4分
所以为等差数列,又,所以,,
∴,
又时,也满足上式,
所以. 8分
因为,,成等比数列,∴, 10分
∴或,又,∴. 12分
若选择③,
因为,所以,
两式相减得, 2分
整理得,
因为,∴,所以是等差数列, 4分
所以, 8分
,
又,,成等比数列,∴, 10分
∴或,又,∴. 12分
19、解:(1)∵PA⊥平面ABCD,BC平面ABCD
∴PA⊥BC
∵ABCD为正方形
∴AB⊥BC
又 PA∩AB=A,PA,AB平面PAB
∴BC⊥平面PAB
∴AE平面PAB
∴AE⊥BC
∵PA=AB,E为线段PB的中点
∴AE⊥PB
又 PB∩BC=B,PB,BC平面PBC
∴AE⊥平面PBC 6分
(2)以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,
设正方形ABCD的边长为2,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0)P(0,0,2)E(1,0,1)
∴,,
设F(2,λ,0)(0≤λ≤2),
∴
设平面AEF的一个法向量为
则
∴
令y1=2,则
∴ 8分
设平面PCD的一个法向量为
则
∴
令y2=1,则
∴ 10分
∵平面AEF与平面PCD所成的锐二面角为30°,
∴,
解得λ=1,
∴当点F为BC中点时,平面AEF与平面PCD所成的锐二面角为30° 12分
20、解(Ⅰ)由题意知对业务满意的有260人,对服务不满意的有100人,得列联表
对服务水平满意人数
对服务水平不满意人数
合计
对业务水平满意人数
180
80
260
对业务水平不满意人数
20
20
40
合计
200
100
300
经计算得,
所以有的把握认为业务水平满意与服务水平满意有关. 2分
(Ⅱ)的可能值为0,1,2.
则,,,
0
1
2
. 6分
(Ⅲ)在业务服务协议终止时,对业务水平和服务水平都满意的客户流失的概率为,只有一项满意的客户流失的概率为,对二者都不满意的客户流失的概率为.
所以从运营系统中任选一名客户流失的概率为, 8分
故在业务服务协议终止时,从运营系统中任选4名客户,至少有2名客户流失的概率为
. 12分
21、解(1)设点坐标为,,
则,
由题意得
解得.∴. 2分
又,∴
∴
∴所求椭圆的方程为: 4分
(2)由题可知直线的斜率存在,则设直线方程为,,坐标为,
解方程组
∴
∴, 6分
又由,∴,
设直线,斜率分别为,,则 7分
∴
即:
∴
∴
化简得:
得:,或 10分
当时,,过点(-2,0),不合题意(舍去)
当时,,过点,
∴直线恒过定点. 12分
22、解(Ⅰ),
, 2分
∵的定义域为.
①即时,在上递减,在上递增,
,无极大值.
②即时,在和上递增,在上递减,
,.
③即时,在上递增,没有极值.
④即时,在和上递增,在上递减,
∴, .
综上可知:时,,无极大值;
时, ,;
时,没有极值;
时,, .
6分
(Ⅱ)设 ,
, 7分
设,则,, ,
∴在上递增,∴的值域为, 9分
①当时,,为上的增函数,
∴,适合条件.
②当时,∵,∴不适合条件.
③当时,对于,,
令,,
存在,使得时,,
∴在上单调递减,
∴,
即在时,,∴不适合条件.
综上,的取值范围为. 12分