- 202.50 KB
- 2021-04-15 发布
- 1、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 2、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报QQ:3215808601
22.2 第5课时 直角三角形相似的判定方法
知|识|目|标
1.通过计算、观察、推理等过程,理解并掌握两个直角三角形相似的判定定理,并能恰当地选择判定三角形相似的方法解决问题.
2.通过对相似三角形判定方法和相似三角形的性质的理解和掌握,灵活选用合适的判定方法解题.
目标一 会用斜边和一直角边对应成比例判定两个直角三角形相似
例1 [教材补充例题]根据下列条件判断Rt△ABC和Rt△A′B′C′是否相似,其中∠C=∠C′=90°.
(1)AC=14 cm,BC=6 cm,A′C′=7 cm,B′C′=3 cm;
(2)AB= cm,AC= cm,A′B′= cm,A′C′= cm.
例2 [教材补充例题]如图22-2-17,已知AB⊥BD,ED⊥BD,B,D分别为垂足,C是线段BD的中点,ED=1,AC=2 ,BD=4.试说明:△ABC∽△CDE.
图22-2-17
【归纳总结】直角三角形相似的判定定理中的“三注意”:
(1)两个三角形必须都是直角三角形才能使用该定理;
(2)注意分清楚直角边的对应关系,若没有明确说明,则需要分类讨论;
(3)相似三角形的判定定理同样适用于直角三角形相似的判定.
目标二 能选用合适的方法判定三角形相似
例3[ 教材补充例题]如图22-2-18,CD是Rt△ABC斜边AB上的高,E为BC的中点,ED的延长线交CA的延长线于点F.
求证:AC·CF=BC·DF.
图22-2-18
【归纳总结】证明“等积式”的“口诀”:
5
等积式化比例式,横找竖看定相似.
不相似,莫生气,等比线来代替.
说明:“横找”即看比例式中两边的比的前项确定的三角形与后项确定的三角形是否相似;“竖看”即看比例式中左边的比的前后两项确定的三角形与右边的比的前后两项确定的三角形是否相似.
知识点一 直角三角形相似的判定定理
(1)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边________________,那么这两个直角三角形相似.
(2)判定直角三角形相似的方法:①定理1,②定理2,③定理3,④斜边和一条直角边对应成比例的两个直角三角形相似.
[点拨] 直角三角形相似的判定方法:
知识点二 三角形相似的判定方法的综合应用
三角形
相似的
判定
思路
有平行截线——选用平行线的性质找等角
有一对等角,找
有两边对应成比例,找
直角三角形,找
等腰三角形,找
(续表)
5
几
种
常
见
的
图
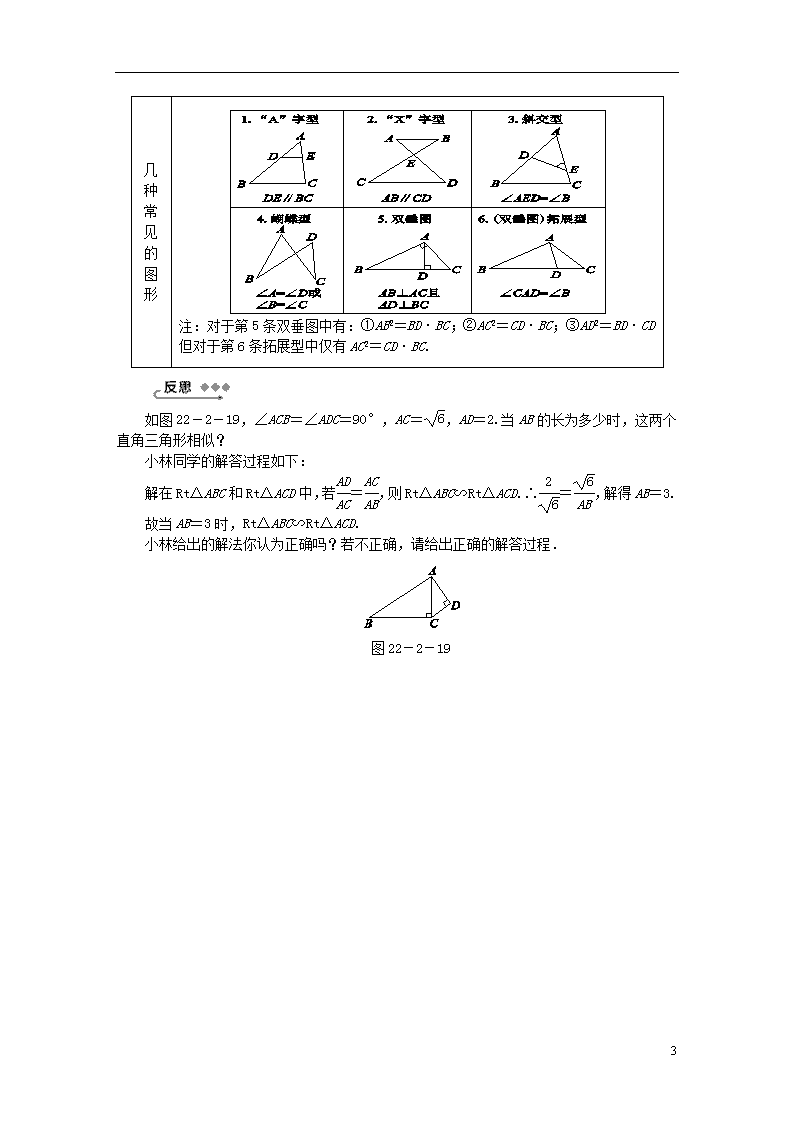
形
注:对于第5条双垂图中有:①AB2=BD·BC;②AC2=CD·BC;③AD2=BD·CD
但对于第6条拓展型中仅有AC2=CD·BC.
如图22-2-19,∠ACB=∠ADC=90°,AC=,AD=2.当AB的长为多少时,这两个直角三角形相似?
小林同学的解答过程如下:
解:在Rt△ABC和Rt△ACD中,若=,则Rt△ABC∽Rt△ACD.∴=,解得AB=3.
故当AB=3时,Rt△ABC∽Rt△ACD.
小林给出的解法你认为正确吗?若不正确,请给出正确的解答过程.
图22-2-19
5
教师详解详析
【目标突破】
例1 [解析] (1)先求出两边成比例,再由夹角相等,即可得出△ABC∽△A′B′C′;
(2)求出斜边和一条直角边对应成比例,即可得出Rt△ABC∽Rt△A′B′C′.
解:(1)∴△ABC∽△A′B′C′.理由如下:
∵==2,==2,∴=.
又∵∠C=∠C′=90°,∴△ABC∽△A′B′C′.
(2)Rt△ABC∽Rt△A′B′C′.理由如下:
∵==,==,∴=.又∠C=∠C′=90°,∴Rt△ABC∽Rt△A′B′C′.
例2 [解析] 要说明△ABC与△CDE相似,通过已知并结合图形,观察可知这两个三角形已经具备一对对应角相等,即∠B=∠D=90°,那么再求出斜边和一条直角边对应成比例即可.
解:∵AB⊥BD,ED⊥BD,
∴∠B=∠D=90°.
又∵C是线段BD的中点,BD=4,
∴BC=CD=2,∴CE==.
∵AC=2 ,BC=2,
∴AC∶CE=BC∶DE=2∶1,
∴△ABC∽△CDE.
例3 证明:∵CD是Rt△ABC斜边AB上的高,E为BC的中点,
∴CE=EB=DE,∴∠B=∠BDE=∠FDA.
∵∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,∴∠FDA=∠ACD.
又∵∠F=∠F,∴△FDA∽△FCD,
∴=.
∵∠ADC=∠CDB=90°,∠ACD=∠B,
∴△ACD∽△CBD,∴=,
∴=,即AC·CF=BC·DF.
【总结反思】
5
[小结] 知识点一 对应成比例
[反思] 不正确,考虑问题不全面,丢掉了一种情况.正确的解答过程如下:
分两种情况考虑:
(1)在Rt△ABC和Rt△ACD中,
若=,则Rt△ABC∽Rt△ACD,
∴=,解得AB=3.
故当AB=3时,Rt△ABC∽Rt△ACD.
(2) 在Rt△ACD中,CD===.若=,则Rt△ABC∽Rt△CAD,∴=,解得AB=3 .故当AB=3或3 时,Rt△ABC与Rt△ACD相似.
5
相关文档
- 信息技术计划总结之初中电教工作总2021-04-15 15:30:472页
- 初中化学九年级上册第五单元化学方2021-04-15 15:30:1820页
- 精编初中师德师风心得体会(三)2021-04-15 15:30:0418页
- 2020年初中班主任年度工作计划范文2021-04-15 15:29:095页
- 2020年国培初中语文培训总结2021-04-15 15:24:555页
- 初中语文多媒体教学课件:9王几何(人2021-04-15 15:22:2517页
- 2021初中英语教师工作计划3篇2021-04-15 15:22:147页
- 初中化学九年级上册第四单元自然界2021-04-15 15:21:1420页
- 冀教初中八年级英语上册英语单词词2021-04-15 15:20:4912页
- 2020初中音乐教师进城考调考试模拟2021-04-15 15:17:375页