- 331.00 KB
- 2024-04-04 发布
- 1、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，可选择认领，认领后既往收益都归您。
- 2、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形，可联系本站下载客服投诉处理。
- 文档侵权举报QQ：3215808601
第25课 三角函数的图象与性质
[最新考纲]
内容
要求
A
B
C
正弦函数、余弦函数、
正切函数的图象与性质
√
1．用五点法作正弦函数和余弦函数的简图
正弦函数y＝sin x，x∈[0,2π]图象的五个关键点是：(0,0)，，(π，0)，，(2π，0)．
余弦函数y＝cos x，x∈[0,2π]图象的五个关键点是：(0,1)，，(π，－1)，，(2π，1)．
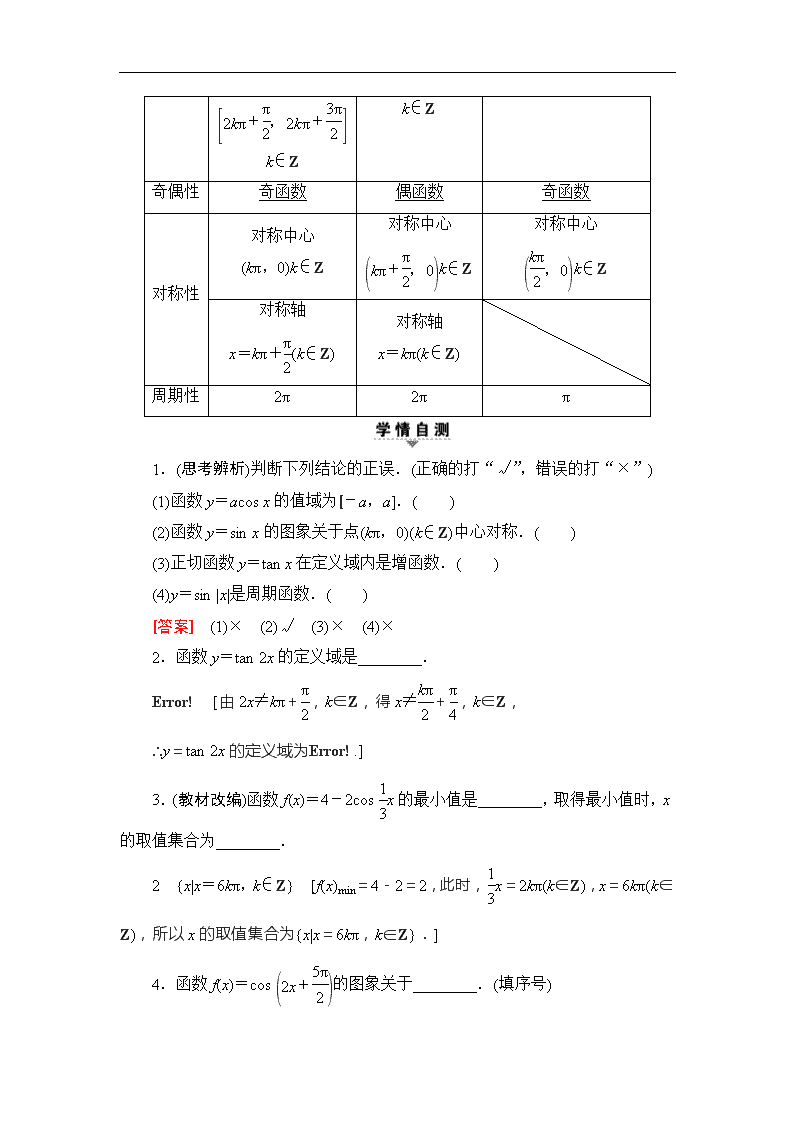
2．正弦函数、余弦函数、正切函数的图象与性质
函数
y＝sin x
y＝cos x
y＝tan x
图象
定义域
R
R
值域
[－1,1]
[－1,1]
R
单调性
递增区间：
k∈Z，
递减区间：
递增区间：
[2kπ－π，2kπ]
k∈Z，
递减区间：
[2kπ，2kπ＋π]
递增区间
(k∈Z)
k∈Z
k∈Z
奇偶性
奇函数
偶函数
奇函数
对称性
对称中心
(kπ，0)k∈Z
对称中心
k∈Z
对称中心
k∈Z
对称轴
x＝kπ＋(k∈Z)
对称轴
x＝kπ(k∈Z)
周期性
2π
2π
π
1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)
(1)函数y＝acos x的值域为[－a，a]．( )
(2)函数y＝sin x的图象关于点(kπ，0)(k∈Z)中心对称．( )
(3)正切函数y＝tan x在定义域内是增函数．( )
(4)y＝sin |x|是周期函数．( )
[答案] (1)× (2)√ (3)× (4)×
2．函数y＝tan 2x的定义域是________．
[由2x≠kπ＋，k∈Z，得x≠＋，k∈Z，
∴y＝tan 2x的定义域为.]
3．(教材改编)函数f(x)＝4－2cos x的最小值是________，取得最小值时，x的取值集合为________．
2 {x|x＝6kπ，k∈Z} [f(x)min＝4－2＝2，此时，x＝2kπ(k∈Z)，x＝6kπ(k∈Z)，所以x的取值集合为{x|x＝6kπ，k∈Z}．]
4．函数f(x)＝cos的图象关于________．(填序号)
①原点对称； ②y轴对称；
③直线x＝对称； ④直线x＝－对称．
① [函数f(x)＝cos＝－sin 2x是奇函数，则图象关于原点对称．]
5．函数y＝sin，x∈[－2π，2π]的单调递增区间是________．
[z＝x＋，函数y＝sin z的单调递增区间为(k∈Z)，由2kπ－≤x＋≤2kπ＋得4kπ－≤x≤4kπ＋，而x∈[－2π，2π]，故其单调递增区间是.]
三角函数的定义域与值域
(1)(2016·全国卷Ⅱ改编)函数f(x)＝cos 2x＋6cos的最大值为________．
(2)函数y＝lg(sin 2x)＋的定义域为________．
(1)5 (2)∪ [(1)∵f(x)＝cos 2x＋6cos＝cos 2x＋6sin x
＝1－2sin2x＋6sin x＝－22＋，
又sin x∈[－1,1]，∴当sin x＝1时，f(x)取得最大值5.
(2)由得
∴－3≤x＜－或0＜x＜，
∴函数y＝lg(sin 2x)＋的定义域为∪.]
[规律方法] 1.三角函数定义域的求法
求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．
2．求三角函数最值或值域的常用方法
(1)直接法：直接利用sin x和cos x的值域求解．
(2)化一法：把所给三角函数化为y＝Asin(ωx＋φ)＋k的形式，由正弦函数单调性写出函数的值域．
(3)换元法：把sin x，cos x，sin xcos x或sin x±cos x换成t，转化为二次函数求解．
[变式训练1] (1)已知函数y＝2cos x的定义域为，值域为[a，b]，则b－a的值是________．
(2)求函数y＝cos2x＋sin x的最大值与最小值. 【导学号：62172138】
(1)3 [∵x∈，∴cos x∈，故y＝2cos x的值域为[－2,1]，
∴b－a＝3.]
(2)令t＝sin x，∵|x|≤，∴t∈，
∴y＝－t2＋t＋1＝－2＋，
∴当t＝时，ymax＝，当t＝－时，ymin＝，
∴函数y＝cos2x＋sin x的最大值为，最小值为.
三角函数的单调性
(1)(2017·苏州模拟)已知ω＞0，函数f(x)＝sin在上单调递减，则ω的取值范围是________．
(2)函数f(x)＝sin的单调减区间为________．
(1) (2)(k∈Z) [(1)由＜x＜π得ω＋＜ωx＋＜πω＋，由题意知⊆，
所以解得≤ω≤.
(2)由已知函数为y＝－sin，欲求函数的单调减区间，只需求y＝sin的单调增区间即可．
由2kπ－≤2x－≤2kπ＋，k∈Z，
得kπ－≤x≤kπ＋，k∈Z.
故所求函数的单调减区间为(k∈Z)．]
[规律方法] 1.求三角函数单调区间的两种方法
(1)求函数的单调区间应遵循简化原则，将解析式先化简，并注意复合函数单调性规律“同增异减”．
(2)求形如y＝Asin(ωx＋φ)(ω＞0)的单调区间时，要视“ωx＋φ”为一个整体，通过解不等式求解．若ω＜0，应先用诱导公式化x的系数为正数，以防止把单调性弄错．
2．已知三角函数的单调区间求参数．先求出函数的单调区间，然后利用集合间的关系求解．
[变式训练2] (1)函数f(x)＝tan的单调递增区间是________．
(2)若函数f(x)＝sin ωx(ω＞0)在区间上单调递增，在区间上单调递减，则ω＝________.
(1)(k∈Z) (2) [(1)由－＋kπ＜2x－＜＋kπ(k∈Z)，
得－＜x＜＋(k∈Z)．
(2)∵f(x)＝sin ωx(ω＞0)过原点，
∴当0≤ωx≤，即0≤x≤时，y＝sin ωx是增函数；
当≤ωx≤，即≤x≤时，y＝sin ωx是减函数．
由f(x)＝sin ωx(ω＞0)在上单调递增，
在上单调递减知，＝，∴ω＝.]
三角函数的奇偶性、
周期性、对称性
角度1 奇偶性与周期性的判断
(1)在函数：①y＝cos|2x|；②y＝|cos x|；③y＝cos2x＋；④y＝tan中，最小正周期为π的所有函数为________．(填序号)
(2)函数y＝1－2sin2是________函数．(填奇偶性)
(1)①②③ (2)奇 [(1)①y＝cos|2x|＝cos 2x，T＝π.
②由图象知，函数的周期T＝π.
③T＝π.
④T＝.
综上可知，最小正周期为π的所有函数为①②③.
(2)y＝1－2sin2＝cos 2＝－sin 2x，所以f(x)是奇函数．]
角度2 求三角函数的对称轴、对称中心
已知函数f(x)＝sin(ωx＋φ)的最小正周期为4π，且对任意x∈R，都有f(x)≤f成立，则下列是f(x)图象的一个对称中心的坐标是________．(填序号) 【导学号：62172139】
①；②；③；④.
① [由f(x)＝sin (ωx＋φ)的最小正周期为4π，得ω＝.因为f(x)≤f恒成立，所以f(x)max＝f，
即×＋φ＝＋2kπ(k∈Z)，
∴φ＝＋2kπ(k∈Z)，由|φ|＜，
得φ＝，故f(x)＝sin.
令x＋＝kπ(k∈Z)，
得x＝2kπ－(k∈Z)，故f(x)图象的对称中心为(k∈Z)，当k＝0时，f(x)图象的一个对称中心的坐标为.]
角度3 三角函数对称性的应用
(1)如果函数y＝3cos(2x＋φ)的图象关于点中心对称，那么|φ|的最小值为________．
(2)已知函数f(x)＝sin x＋acos x的图象关于直线x＝对称，则实数a的值为________．
(1) (2)－ [(1)由题意得3cos
＝3cos＝3cos＝0，
∴＋φ＝kπ＋，k∈Z，
∴φ＝kπ－，k∈Z，取k＝0，得|φ|的最小值为.
(2)由x＝是f(x)图象的对称轴，
可得f(0)＝f，
即sin 0＋acos 0＝sin＋acos，
解得a＝－.]
[规律方法] 1.对于函数y＝Asin(ωx＋φ)，其对称轴一定经过图象的最高点或最低点，对称中心一定是函数的零点，因此在判断直线x＝x0或点(x0,0)是不是函数的对称轴或对称中心时，可通过检验f(x0)的值进行判断．
2．求三角函数周期的方法：
(1)利用周期函数的定义．
(2)利用公式：y＝Asin(ωx＋φ)和y＝Acos(ωx＋φ)的最小正周期为，y＝tan(ωx＋φ)的最小正周期为.
(3)借助函数的图象．
[思想与方法]
1．讨论三角函数性质，应先把函数式化成y＝Asin(ωx＋φ)(ω＞0)的形式，再用换元法令t＝ωx＋φ，将其转化为研究y＝sin t的性质．
2．求三角函数值域(最值)的常用方法：
(1)将函数变形化为y＝Asin(ωx＋φ)＋k的形式，逐步分析ωx＋φ的范围，根据正弦函数单调性写出函数的值域(最值)．
(2)换元法：把sin x或cos x看作一个整体，可化为求二次函数在区间上的值域(最值)问题．
3．若f(x)＝Asin(ωx＋φ)(A＞0，ω＞0)，则
(1)f(x)为偶函数的充要条件是φ＝＋kπ(k∈Z)；
(2)f(x)为奇函数的充要条件是φ＝kπ(k∈Z)．
[易错与防范]
1．闭区间上最值或值域问题，首先要在定义域基础上分析单调性，含参数的最值问题，要讨论参数对最值的影响．
2．求y＝Asin(ωx＋φ)(A＞0)的单调区间，要注意ω的正负，只有当ω＞0时，才能将“ωx＋φ”整体代入相应单调区间．
3．利用换元法求三角函数最值时，注意cos x(或sin x)的有界性．
4．正、余弦函数的图象既是轴对称图形，又是中心对称图形且最值点在对称轴上；正切函数的图象只是中心对称图形．
课时分层训练(二十五)
A组 基础达标
(建议用时：30分钟)
一、填空题
1．函数y＝的定义域为________．
(k∈Z) [由cos x－≥0，得cos x≥，∴2kπ－≤x≤2kπ＋，k∈Z.]
2．已知函数f(x)＝sin(ω＞0)的最小正周期为π，则f＝________.
1 [由题设知＝π，所以ω＝2，f(x)＝sin，所以f＝sin
＝sin ＝1.]
3．函数y＝tan的图象与x轴交点的坐标是________.
【导学号：62172140】
，k∈Z [由2x＋＝kπ(k∈Z)得，x＝－(k∈Z)，
∴函数y＝tan的图象与x轴交点的坐标是，k∈Z.]
4．函数f(x)＝sin(－2x)的单调增区间是________．
(k∈Z) [由f(x)＝sin(－2x)＝－sin 2x,2kπ＋≤2x≤2kπ＋得kπ＋≤x≤kπ＋(k∈Z)．]
5．已知函数f(x)＝2sin(ωx＋φ)，对于任意x都有f＝f，则f的值为________．
2或－2 [∵f＝f，
∴x＝是函数f(x)＝2sin(ωx＋φ)的一条对称轴，
∴f＝±2.]
6．下列函数中，最小正周期为π且图象关于原点对称的函数是________．(填序号) 【导学号：62172141】
①y＝cos ；
②y＝sin ；
③y＝sin 2x＋cos 2x；
④y＝sin x＋cos x.
① [y＝cos ＝－sin 2x，最小正周期T＝＝π，且为奇函数，其图象关于原点对称，故①正确；
y＝sin ＝cos 2x，最小正周期为π，且为偶函数，其图象关于y轴对称，故②不正确；
③，④均为非奇非偶函数，其图象不关于原点对称，故③，④不正确．]
7．若函数y＝cos(ω∈N＋)图象的一个对称中心是，则ω的最小值为________．
2 [由题意知＋＝kπ＋(k∈Z)⇒ω＝6k＋2(k∈Z)，又ω∈N＋，∴ωmin＝2.]
8．若函数f(x)＝sin－cos ωx(ω＞0)的图象相邻两个对称中心之间的距离为，则下列是f(x)的一个单调递增区间的是________．(填序号)
①；②；③；④.
① [依题意得f(x)＝sin ωx－cos ωx＝sin的图象相邻两个对称中心之间的距离为，于是有T＝＝2×＝π，ω＝2，f(x)＝sin.当2kπ－≤2x－≤2kπ＋，即kπ－≤x≤kπ＋，k∈Z时，f(x)＝sin单调递增．因此结合各选项知f(x)＝sin的一个单调递增区间为.]
9．函数y＝cos 2x＋sin2x，x∈R的值域是________．
[0,1] [因为y＝cos 2x＋sin2x
＝1－2sin2x＋sin2x
＝1－sin2x.
又sin2x∈[0,1]，所以1－sin2x∈[0,1]．
故y∈[0,1]．]
10．(2017·如皋中学高三第一次月考)已知函数f(x)＝sin x，g(x)＝sin，直线x＝m与f(x)、g(x)的图象分别交于M、N两点，则MN
的最大值是________．
[∵g(x)＝sin＝cos x，
由题意可知MN＝|sin x－cos x|＝.
∵x∈R，∴|f(x)－g(x)|∈[0，]．
故M，N的距离的最大值为.]
二、解答题
11．(2016·北京高考)已知函数f(x)＝2sin ωxcos ωx＋cos 2ωx(ω>0)的最小正周期为π.
(1)求ω的值；
(2)求f(x)的单调递增区间．
[解] (1)因为f(x)＝2sin ωxcos ωx＋cos 2ωx
＝sin 2ωx＋cos 2ωx＝sin，
所以f(x)的最小正周期T＝＝.
依题意，得＝π，解得ω＝1.
(2)由(1)知f(x)＝sin.
函数y＝sin x的单调递增区间为(k∈Z)．
由2kπ－≤2x＋≤2kπ＋(k∈Z)，
得kπ－≤x≤kπ＋(k∈Z)．
所以f(x)的单调递增区间为(k∈Z)．
12．已知函数f(x)＝(sin x＋cos x)2＋cos 2x.
(1)求f(x)的最小正周期；
(2)求f(x)在区间上的最大值和最小值. 【导学号：62172142】
[解] (1)因为f(x)＝sin2x＋cos2x＋2sin x·cos x＋cos 2x＝1＋sin 2x＋cos 2x＝sin＋1，
所以函数f(x)的最小正周期为T＝＝π.
(2)由(1)的计算结果知，f(x)＝sin＋1.
当x∈时，2x＋∈，由正弦函数y＝sin x在上的图象知，当2x＋＝，即x＝时，f(x)取最大值＋1；
当2x＋＝，即x＝时，f(x)取最小值0.
综上，f(x)在上的最大值为＋1，最小值为0.
B组 能力提升
(建议用时：15分钟)
1．已知函数y＝cos x与y＝sin(2x＋φ)(0≤φ＜π)，它们的图象有一个横坐标为的交点，则φ的值是________．
[由题意cos ＝sin，
即sin＝，＋φ＝kπ＋(－1)k·(k∈Z)．因为0≤φ＜π，所以φ＝.]
2．已知函数f(x)＝3sin(ω>0)和g(x)＝2cos(2x＋φ)＋1的图象的对称轴完全相同，若x∈，则f(x)的取值范围是________．
[依题意得ω＝2，所以f(x)＝3sin.
因为x∈，所以2x－∈，
所以sin∈，
所以f(x)∈.]
3．已知函数f(x)＝sin(ωx＋φ)的最小正周期为π.
(1)求当f(x)为偶函数时φ的值；
(2)若f(x)的图象过点，求f(x)的单调递增区间．
[解] ∵f(x)的最小正周期为π，则T＝＝π，∴ω＝2，
∴f(x)＝sin(2x＋φ)．
(1)当f(x)为偶函数时，f(－x)＝f(x)，
∴sin(－2x＋φ)＝sin(2x＋φ)，
将上式展开整理得sin 2xcos φ＝0，
由已知上式对∀x∈R都成立，
∴cos φ＝0.∵0＜φ＜，∴φ＝.
(2)∵f(x)的图象过点时，sin＝，
即sin＝.
又∵0＜φ＜，∴＜＋φ＜π，
∴＋φ＝，φ＝，
∴f(x)＝sin.
令2kπ－≤2x＋≤2kπ＋，k∈Z，
得kπ－≤x≤kπ＋，k∈Z，
∴f(x)的单调递增区间为，k∈Z.
4．设函数f(x)＝sin2ωx＋2sin ωx·cos ωx－cos2ωx＋λ(x∈R)的图象关于直线x
＝π对称，其中ω，λ为常数，且ω∈.
(1)求函数f(x)的最小正周期；
(2)若y＝f(x)的图象经过点，求函数f(x)的值域．
[解] (1)因为f(x)＝sin2ωx－cos2ωx＋2sin ωx·cos ωx＋λ＝－cos 2ωx＋sin 2ωx＋λ＝2sin＋λ，
由直线x＝π是y＝f(x)图象的一条对称轴，可得sin＝±1.
所以2ωπ－＝kπ＋(k∈Z)，即ω＝＋(k∈Z)．
又ω∈，k∈Z，所以ω＝.
所以f(x)的最小正周期是.
(2)由y＝f(x) 的图象过点，
得f＝0，
即λ＝－2sin＝－2sin＝－，即λ＝－.
故f(x)＝2sin－，函数f(x)的值域为[－2－，2－]．
