内蒙古乌兰察布市北京八中乌兰察布分校2018-2019学年高一下学期教学质量调研三数学试题 19页

北京八中乌兰察布分校 ‎2018-2019学年第二学期第三次质量调研考试 高一年级数学试题 一、选择题：（本大题共12小题。每小题5分，满分60分。在每小题给出的四个选项中，只有一个选项是符合题意的。）‎ ‎1.已知全集，集合，，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据集合补集及交集的定义即可求解。‎ ‎【详解】由题可得 ，，所以，‎ 故答案选B。‎ ‎【点睛】本题主要考查集合间的运算，属于基础题。‎ ‎2.已知角的终边经过点（1，-2），则（ ）‎ A. B. ‎-2 ‎C. D. 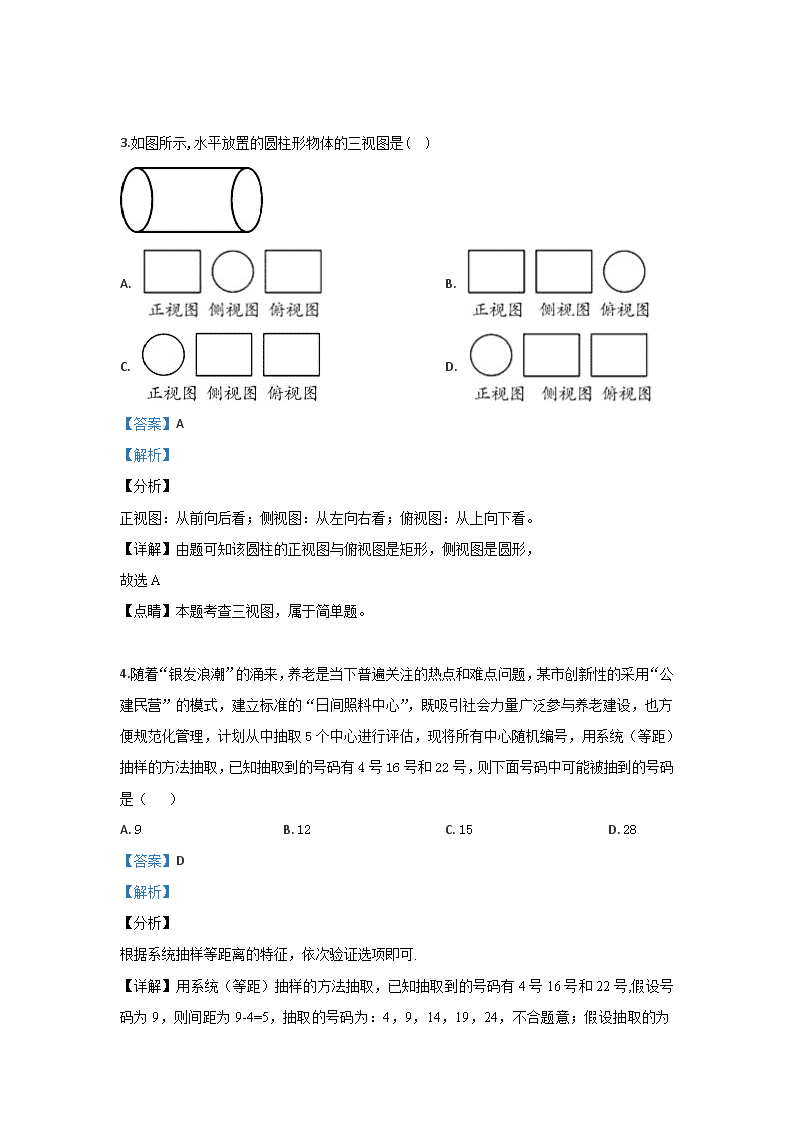‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 利用三角函数的定义，即可求解，得到答案．‎ ‎【详解】因为角的终边经过点，由三角函数的定义，可得，故选D.‎ ‎【点睛】本题主要考查了三角函数的定义的应用，其中解答中熟记三角函数的定义是解答的关键，着重考查了推理与运算能力．‎ ‎3.如图所示,水平放置的圆柱形物体的三视图是( )‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 正视图：从前向后看；侧视图：从左向右看；俯视图：从上向下看。‎ ‎【详解】由题可知该圆柱的正视图与俯视图是矩形，侧视图是圆形，‎ 故选A ‎【点睛】本题考查三视图，属于简单题。‎ ‎4.随着“银发浪潮”的涌来，养老是当下普遍关注的热点和难点问题，某市创新性的采用“公建民营”的模式，建立标准的“日间照料中心”，既吸引社会力量广泛参与养老建设，也方便规范化管理，计划从中抽取5个中心进行评估，现将所有中心随机编号，用系统（等距）抽样的方法抽取，已知抽取到的号码有4号16号和22号，则下面号码中可能被抽到的号码是（ ）‎ A. 9 B. ‎12 ‎C. 15 D. 28‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据系统抽样等距离的特征，依次验证选项即可.‎ ‎【详解】用系统（等距）抽样的方法抽取，已知抽取到的号码有4号16号和22号,假设号码为9，则间距为9-4=5，抽取的号码为：4，9，14，19，24，不合题意；假设抽取的为 ‎12，则4，16，12，22，间距分别为8，4，6，再插入一个数也不会等间距，故不合题意；如果插入的为15，则15，16相邻，不可能成立，故舍去；假设号码为28，则这五个数为：4，10，16，22，28.满足题意.‎ 故答案为：D.‎ ‎【点睛】这个题目考查了系统抽样的概念属于基础题.‎ ‎5.从中任取一个数x，从中任取一个数y，则使的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 在平面直角坐标系中作出图形，则x∈[0，2]，y∈[0，3]的平面区域为矩形，符合条件x2+y2≤4的区域为以原点为圆心，2为半径的扇形内部，则扇形面积与矩形面积的比为概率 ‎【详解】在平面直角坐标系中作出图形，如图所示，‎ 则x∈[0，2]，y∈[0，3]的平面区域为矩形OABC，‎ 符合条件x2+y2≤4的区域为以原点为圆心，‎ ‎2为半径的扇形OAD内部，‎ ‎∴P（x2+y2≤4）；‎ 故选：D．‎ ‎【点睛】本题考查了几何概型的概率计算，正确作出几何图形是解题的关键．‎ ‎6.已知函数 ，则的图象过定点（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 令，则，即所以函数的图象过定点，得到答案.‎ ‎【详解】由题意知，函数，令，则，‎ 所以函数的图象过定点，故选B.‎ ‎【点睛】本题主要考查了指数函数的性质的应用，其中解答中熟记指数函数的性质是解答的关键，着重考查了运算与求解能力，属于基础题.‎ ‎7.如图是一个半径为R的扇形，它的周长为4R，则这个扇形所含弓形（阴影区域）的面积是（ ）‎ A. ‎ B. ‎ C. ‎ D. ‎ ‎【答案】D ‎【解析】‎ 分析】‎ 通过扇形的周长，求出扇形的弧长，求出扇形的圆心角，然后求出扇形的面积，三角形的面积，即可得到这个扇形所含弓形的面积．‎ ‎【详解】，‎ S弓形＝S扇形﹣S三角形＝R2﹣sin1•cos1•R2‎ 故选：D．‎ ‎【点睛】本题是基础题，考查扇形的面积公式的应用，弓形面积的求法，考查计算能力，注意弓形面积的求法．‎ ‎8.已知，，则的值为 （ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 先求出，再根据得到，进而可得所求值．‎ ‎【详解】由题意得，‎ ‎∵，‎ ‎∴，‎ ‎∴．‎ 故选B．‎ ‎【点睛】本题考查同角三角函数关系式，解题时注意已知中的一个可以求出其他两个，其中关键是根据的范围得到这三个值的符号，属于基础题．‎ ‎9.已知，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由，利用诱导公式，得，即可求解，得到答案.‎ ‎【详解】由题意，可知，‎ 由三角函数的诱导公式，因为，‎ 则，故选C.‎ ‎【点睛】本题主要考查了三角函数的诱导公式的化简求值问题，其中解答中熟记三角函数的诱导公式，准确计算是解答的关键，着重考查了推理与计算能力，属于基础题.‎ ‎10.要得到函数的图象，只需将函数的图象（　　）‎ A. 向右平移个单位 B. 向右平移个单位 C. 向左平移个单位 D. 向左平移个单位 ‎【答案】D ‎【解析】‎ ‎【分析】‎ 利用左加右减的平移原则可对ABCD四个选项逐一排查，如A选项中=2x，即可得到答案．‎ ‎【详解】=cos2x．‎ ‎=cos（2x-）；‎ ‎=-cos2x；‎ ‎=cos（2x+）；‎ 可排除A、B、C；‎ 故选D．‎ ‎【点睛】本题考查函数y=Asin（ωx+φ）的图象变换，关键是掌握左加右减的平移原则及平移单位，属于中档题．‎ ‎11.记不超过实数的最大整数为，则函数称作取整函数，取整函数在科学和工程上有广泛应用．下面的程序框图是与取整函数有关的求和问题，若输出的的值为5，则判断框内填入的条件可以是( )‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 依次运行框图中的程序，结合输出的结果可得判断框中的条件．‎ ‎【详解】依次执行程序框图中的程序，可得：‎ 第一次循环，，，不满足条件，继续运行；‎ 第二次循环，，，不满足条件，继续运行；‎ 第三次循环，，，不满足条件，继续运行；‎ 第四次循环，，，不满足条件，继续运行；‎ 第五次循环，，，不满足条件，继续运行；‎ 第六次循环，，，满足条件，退出循环，输出的值为5，‎ 结合各选项可得判断框中的条件为．‎ 故选B．‎ ‎【点睛】程序框图的补全及逆向求解问题思路：①先假设参数的判断条件满足或不满足；②运行循环结构，一直到运行结果与题目要求的输出结果相同为止；③根据此时各个变量的值，补全程序框图．此类试题要求学生要有比较扎实的算法初步的基本知识，以及综合分析问题和解决问题的能力，要求较高，属中档题．‎ ‎12.函数 的一部分图像如图所示，则（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ 由图可知,,排除选项,由,排除选项,故选.‎ 二、填空题：（本大题共4小题。每小题5分，满分20.）‎ ‎13.两平行直线与之间的距离为________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 化为，利用平行线的距离公式可得结果.‎ ‎【详解】化为，‎ 由平行线的距离公式可得，‎ 两平行直线与之间的距离为，‎ 故答案为.‎ ‎【点睛】本题主要考查两平行线的距离公式，属于基础题.利用两平行线的距离公式解题时，一定要注意两直线方程中的系数分别相等.‎ ‎14.已知为钝角，，则____________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 利用三角函数的基本关系式，求得，再利用三角函数的诱导公式，即可求解，得到答案．‎ ‎【详解】由题意知，角为钝角，且，‎ 所以，‎ 又由.‎ ‎【点睛】本题主要考查了利用三角函数的诱导公式和基本关系式的应用化简、求值问题，其中解答中熟记三角函数的诱导公式和基本关系式，准确运算是解答的关键，着重考查了运算与求解能力，属于基础题．‎ ‎15.若函数，其中都非零实数，且满足，则__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由利用诱导公式求得，再利用诱导公式可求得的值.‎ ‎【详解】，‎ ‎，故答案为.‎ ‎【点睛】本题主要考查诱导公式的应用，意在考查灵活应用所学知识解答问题的能力，属于中档题.‎ ‎16.关于下列命题：‎ ‎①若是第一象限角，且，则；‎ ‎②函数是偶函数；‎ ‎③函数的一个对称中心是；‎ ‎④函数在上是增函数，‎ 所有正确命题的序号是_____．‎ ‎【答案】②③‎ ‎【解析】‎ ‎【分析】‎ 结合相关知识对给出的每个选项分别进行分析、判断可得正确的命题．‎ ‎【详解】对于①，若α，β是第一象限角，且α>β，可令α=390°，β=30°，则sin α=sin β，所以①错误；‎ 对于②，函数y=sin=-cos πx，f(x)=-cos(πx)=f(x)，则为偶函数，所以②正确；‎ 对于③，令2x-=kπ，解得x=(k∈Z)，所以函数y=sin的对称中心为，‎ 当k=0时，可得对称中心为，所以③正确；‎ 对于④，函数，当时，，所以函数在区间上单调递减，所以④不正确．‎ 综上，命题②③正确．‎ ‎【点睛】本题综合考查三角函数的有关内容，考查综合运用和解决问题的能力，解题时可根据题中的要求分别进行求解，但由于涉及的内容较多，所以解题时要注意结果的正确性．‎ 三、解答题：（本大题共6小题。17题10分，其余每小题12分，满分70.）‎ ‎17.已知函数 ‎（1）用五点法作出函数一个周期的简图；‎ ‎（2）写出函数的值域与单调区间。‎ ‎【答案】（1）见解析；（2）值域为，单调增区间为：（），减区间为：（）‎ ‎【解析】‎ ‎【分析】‎ ‎(1)本题首先可以根据函数解析式找出函数上的点、、、、，然后根据五点作图法即可得出结果；‎ ‎(2)本题首先可根据函数的图像得出函数的值域，然后根据正弦函数的单调性即可得出结果。‎ 详解】(1)根据函数解析式可知，‎ 函数过点，，，，，‎ 如图所示，可通过五点作图法绘出图像。‎ ‎(2)根据(1)可知：‎ 函数的最大值为，最小值为，故值域为，‎ 当，即时，‎ 函数是增函数；‎ 当，即时，‎ 函数是减函数。‎ ‎【点睛】本题考查三角函数的五点作图法、三角函数的值域以及三角函数的单调性，正弦函数的单调递增区间为，单调递减区间为，考查学生的绘图能力，体现了基础性，是简单题。‎ ‎18.已知，.‎ ‎（1）求的值；‎ ‎（2）求的值.‎ ‎【答案】(1) (2)‎ ‎【解析】‎ 分析：（1）由已知可得，求得或，又由，即可求得.‎ ‎（2）根据诱导公式，化简原式,即可求解.‎ 详解：（1）由已知可得，，‎ 即或.‎ 又，所以为所求.‎ ‎（2）‎ ‎ .‎ 点睛：本题主要考查了三角函数的化简求值，其中熟记诱导公式的应用是解答本题的关键，着重考查了推理与运算能力，属于基础题.‎ ‎19.已知圆，圆，直线l过点．‎ 若直线l被圆所截得的弦长为，求直线l的方程；‎ 若圆P是以为直径的圆，求圆P与圆的公共弦所在直线方程．‎ ‎【答案】（1）或；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据题意，可得圆心C1（0，0），半径r1＝2，可设直线l的方程为x﹣1＝m（y﹣2），即x﹣my+‎2m﹣1＝0，由点到直线的距离公式和圆的弦长公式，解方程可得m，进而得到所求直线方程；‎ ‎（2）根据题意，求得圆心C2的坐标，结合M的坐标可得圆P的方程，联立圆C2与圆P的方程，作差可得答案．‎ ‎【详解】根据题意，圆，其圆心，半径，‎ 又直线l过点且与圆相交，‎ 则可设直线l的方程为，即，‎ 直线l被圆所截得的弦长为，则圆心到直线的距离，‎ 则有，解可得：或；则直线l的方程为或：‎ 根据题意，圆，圆心为，‎ 其一般式方程为，‎ 又由，圆P是以为直径的圆，则圆P的方程为：，变形可得：，‎ 又由，作差可得：．‎ 所以圆P与圆的公共弦所在直线方程为 ‎【点睛】本题考查直线与圆的方程的应用，涉及直线与圆、圆与圆的位置关系，属于综合题．‎ ‎20.已知角，且满足，‎ ‎（1）求的值； ‎ ‎（2）求的值。‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用三角函数的基本关系式，求得，得出，再由三角函数的基本关系式，即可求解.‎ ‎（2）由（1）得，再由，即可求解.‎ ‎【详解】（1）由题意，因为角，且满足，‎ 则，‎ 解得，所以，所以，‎ 所以，‎ 所以 ‎（2）由（1）知，，即，‎ 所以.‎ ‎【点睛】本题主要考查了三角函数的基本关系式化简求值，其中解答中熟记同角三角函数的基本关系式，合理运算与化简是解答的关键，着重考查了推理与运算能力，属于基础题.‎ ‎21.已知．‎ ‎（1）求函数的单调递增区间与对称轴方程；‎ ‎（2）当时，求的最大值与最小值．‎ ‎【答案】（1）单调递增区间为，．对称轴方程为，其中． ‎ ‎（2）的最大值为2，最小值为–1．‎ ‎【解析】‎ ‎【分析】‎ ‎(1)先将函数表达式化简得到，由解得x的范围；（2）根据三角函数的性质得到最值.‎ ‎【详解】（1）因为，‎ 由，‎ 求得，k∈Z，‎ 可得函数f（x）的单调递增区间为，k∈Z．‎ 由，求得，k∈Z．‎ 故f（x）的对称轴方程为，其中k∈Z．‎ ‎（2）因为，所以，故有，‎ 故当即x=0时，f（x）的最小值为–1，‎ 当即时，f（x）的最大值为2．‎ ‎【点睛】已知三角函数解析式求单调区间：①求函数的单调区间应遵循简单化原则，将解析式先化简，并注意复合函数单调性规律“同增异减”；②求形如y=Asin（ωx＋φ）（其中ω>0）的单调区间时，要视“ωx＋φ”为一个整体，通过解不等式求解．但如果ω<0，那么一定先借助诱导公式将ω化为正数，防止把单调性弄错；③若ω<0，利用诱导公式二把y＝Asin(ωx＋φ)中x的系数化为大于0的数．‎ ‎22.某学校为担任班主任的教师办理手机语音月卡套餐，为了解通话时长，采用随机抽样的方法，得到该校100位班主任每人的月平均通话时长（单位：分钟）的数据，其频率分布直方图如图所示，将频率视为概率.‎ ‎（1）求图中的值；‎ ‎（2）估计该校担任班主任的教师月平均通话时长的中位数；‎ ‎（3）在，这两组中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求抽取的2人恰在同一组的概率.‎ ‎【答案】(1) (2)390分钟. (3) ‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据频率分布直方图中所有矩形的面积和为1，列出方程，即可求解；‎ ‎（2）设该校担任班主任的教师月平均通话时长的中位数为，根据频率分布直方图的中位数的计算方法，即可求解.‎ ‎（3）根据分层抽样，可得在内抽取人，分别记为，在内抽取2人，记为，利用古典概型及其概率计算公式，即可求解.‎ ‎【详解】（1）依题意，根据频率分布直方图的性质，可得：‎ ‎，解得.‎ ‎（2）设该校担任班主任的教师月平均通话时长的中位数为.‎ 因为前2组的频率之和为，‎ 前3组的频率之和为，‎ 所以，由，得.‎ 所以该校担任班主任的教师月平均通话时长的中位数为390分钟.‎ ‎（3）由题意，可得在内抽取人，分别记为，‎ 在内抽取2人，记为，‎ 则6人中抽取2人的取法有：，，，，，，，，，，，，，，，共15种等可能的取法.‎ 其中抽取的2人恰在同一组的有，，，，，，，共7种取法，‎ 所以从这6人中随机抽取的2人恰在同一组的概率.‎ ‎【点睛】本题主要考查了频率分布直方图的应用，以及古典概型及其概率的计算，其中解答中熟记频率分布直方图的相关性质，合理利用古典概型及其概率的计算公式，准确计算是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.‎