- 557.50 KB
- 2024-02-17 发布
阆中中学校2018年秋高2017级期中教学质量检测
数学试题(理科)
(总分:150分 时间:120分钟 )
注意事项:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,满分150分,考试时间l20分钟。考生作答时,将答案答在答题卡上(答题注意事项见答题卡),在本试卷上答题无效。考试结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,
只有一项是符合题目要求的)
1. 如图所示,正方体-的棱长为1,则点的坐标是
A.(1,0,0) B.(1,0,1)
C.(1,1,1) D.(1,1,0)
2. 直线的倾斜角为( )
A.30° B.60°
C.120° D.150°
3. 某校老年、中年和青年教师的人数见下表,采用分层抽样的
方法调查教师的身体健康状况,在抽取的样本中,若青年教
师有320人,则该样本中的老年教师人数为( )
类别
人数
老年教师
900
中年教师
1800
青年教师
1600
合计
4300
A.90 B.100 C.180 D.300
4. 圆的圆心到直线的距离为1,则( )
A. B. C. D.2
5. 光线自点射到后被轴反射,则反射光线所在直线与圆( )
A.相离 B.相切 C.相交且过圆心 D.相交但不过圆心
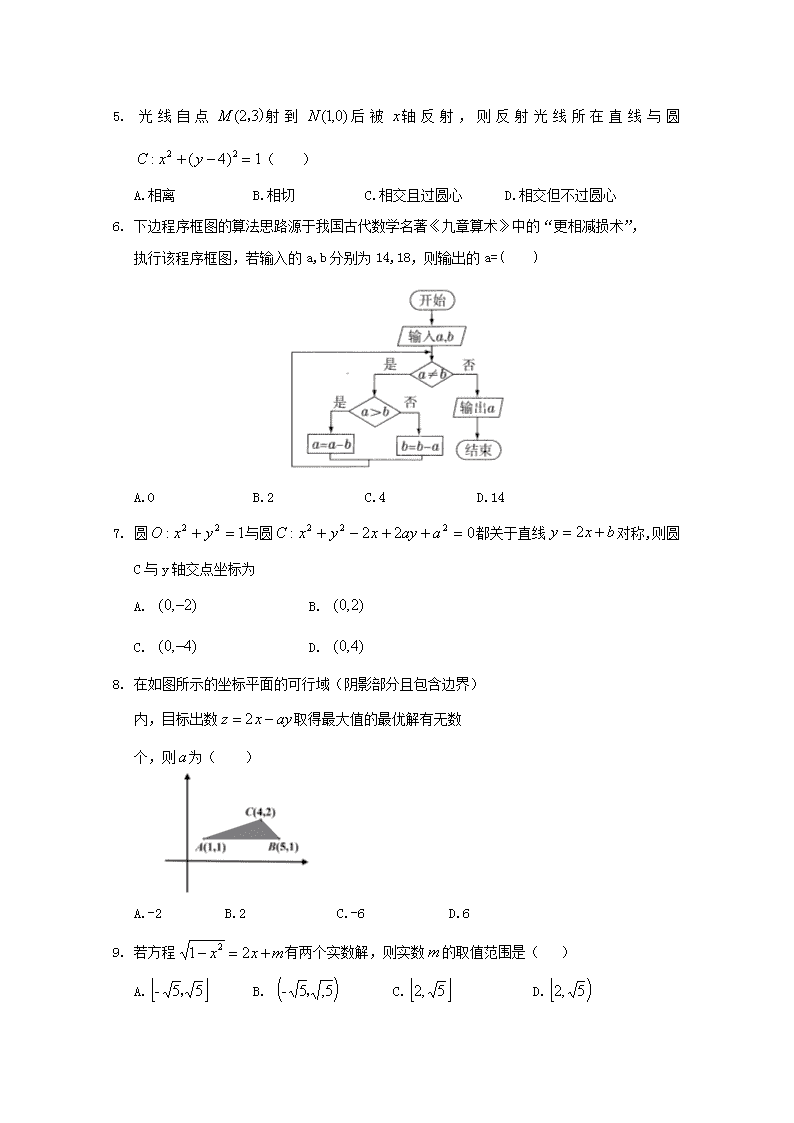
6. 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,
执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )
A.0 B.2 C.4 D.14
7. 圆与圆都关于直线对称,则圆C与y轴交点坐标为
A. B.
C. D.
8. 在如图所示的坐标平面的可行域(阴影部分且包含边界)
内,目标出数取得最大值的最优解有无数
个,则为( )
A.-2 B.2 C.-6 D.6
9. 若方程有两个实数解,则实数的取值范围是( )
A. B. C. D.
10.过点作圆的两条切线,切点分别为A,B,则直线AB的方程为( )
A. B. C. D.
11.在圆内,过点P有n条弦的长度成等差数列,最短弦长为数列的首项,最长弦为,若公差,那么的取值集合为( )
A. B. C. D.
12.在矩形中,,动点P在以点C为圆心且与BD相切的圆上,若,则的最大值为( )
A.3 B. C. D.2
二、填空题(本大题共4个小题,每小题5分,共20分)
13. 若直线与直线垂直,且_____________.
14. 把二进制数化为十进制数是________________.
15. 总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行第5列的数字开始向右读,则选出来的第5个个体的编号为_____________.
7816 6572 0802 6314 0702 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
16. 设满足约束条件,若目标函数的最大值为12,则的最小值为_________________.
三、解答题(本大题共6个小题,共70分)
17.(本小题10分)直线与的交点为P,直线过点P且与直线平行.
(1)求直线的方程;
(2)若点到直线的距离为,求实数的值.
18.(本小题12分)如图所示的程序框图的输入值
(1)当输入的时,求输出的的值;
(2)写出关于的函数解析式并求的最大值.
19.(本小题12分)已知的三顶点坐标分别为:,,的外接圆为圆M.
(1)求圆M的方程;
(2)已知过点的直线被圆M截得的弦长为,求直线的一般式方程.
20.(本小题12分)一元二次方程有两个根,一个根在区间(0,1)内,
另一个根在区间(1,2)内,求:
(1)点对应的区域的面积;
(2)的取值范围.
21.(本小题12分)某研究所计划利用“神十”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A,B,该所要根据该产品的研制成本、产品质量、搭载实验费用和预计产生的利益来决定具体搭载安排,有关数据如下表:
每件产品A
每件产品B
研制成本、搭载费用之和(万元)
20
30
计划最大资金额300万元
产品重量(千克)
10
5
最大搭载重量110千克
预计收益(万元)
80
60
分别用x,y表示搭载新产品A,B的件数,总收益用Z表示.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别搭载新产品A,B各多少件,才能使总预计收益达到最大?并求出此最大收益.
22. (本小题12分)已知圆M的半径为3,圆心在轴正半轴上,直线
与圆M相切.
(1)求圆M的标准方程;
(2)过点的直线L与圆M交于不同的两点,,而且满足
,求直线L的方程.
阆中中学校2018年秋高2017级期中教学质量检测
数学试题答案(理科)
1-5:CDCAD 6-10:BBADA 11-12: AA
13.2 14.51 15.01 16.
17.(1)由得,即 (3分)
∵
∴的方程为
即: (6分)
(2)∵,∴ (10分)
18. (1)当时, (4分)
(2) (8分)
∴函数在[-1,0)上单调递减,[0,3]上单调递增.
又∵时,;时,
∴ (12分)
19.设外接圆M的方程:
则有,解之得
则外接圆M的方程:. (6分)
(2)由(1)及题意知圆心到直线的距离
①当直线的斜率不存在时,符合题意 (8分)
②当直线的斜率存在时,设直线即
∴,解之得 (10分)
∴
综上,直线的一般式方程为:. (12分)
20.解:(1)设
∵方程的一个根在区间(0,1)内,另一个根在区间(1,2)内
∴可得 (2分)
作出满足上述不等式组对应的点所在的平面区域,得到及其内部,即如图所示的阴影部分(不含边界)
(4分)
其中
∴即为点对应的区域的面积.(6分)
(2)设点为区间内的任意一点
可得,表示区域内的点D、E之间的距离的平方
运动点E,可得当E在C点时满足
(9分)
在当E在A点满足 (11分)
由此可得取值范围为:(8,17). (12分)
21.(1)由已知满足的数学关系式为,且(4分)
该二元一次不等式组所表示的区域为图中的阴影部分.
(6分)
(2)设最大收益为万元,则目标函数 (8分)
作出直线并平移,由图像知,
当直线经过M点时,能取到最大值.
由是最优解. (11分)
所以(万元)
答:搭载A产品9件,B产品4件,能使总预计收益达到最大值,最大预计收益为960万元 (12分)
22.(1)设圆心为
∵直线与圆M相切,
∴,解得或(舍去), (3分)
所以圆的方程为 (5分)
(2) 当直线L的斜率不存在时,直线,
则,,此时满足条件,
(7分)
当直线L的斜率存在时,设直线
由消去,得
整理得:
所以 (9分)
由已知得:
整理得:
把值代入到方程(1)中的判别式
中,
判别式的值为正数,所以,
所以直线L为:
即 (11分)
综上:直线L为:
(12分)