2011初三数学二模题答案-燕山 4页

‎ 燕山初四数学二模评卷参考2011.6.2‎ 一、 ACBD　BCDB 二、 题号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 x ≠-3‎ ‎6，4.4‎ ‎1+， 1+‎ 三、13.原式= m（9x4-6 x2+1） ………………………………………1分 = m (3 x2-1)2 ………………………………………………3分 ‎ = m (x+1)2 (x-1) 2 . ………………………………………………5分 ‎ 14.解①得 x<3； ……………………………………………1分 解②得 x-2 . ………………………………………………2分 ‎ ∴ 不等式组的解集是-2x<3. ……………………………………………3分 ‎ ∴ 不等式组的非负整数解是0，1，2 . ………………………………………5分 ‎ 15. (x+1)2=(x-2) (x+1)-(x-2), ……………………………………………1分 ‎ x2+2x+1= x2-x-2 -x +2, …………………………………………2分 ‎ 4x=-1, ……………………………………………3分 ‎ x= -. ……………………………………………4分 ‎ 经检验：x= -是原分式方程的解. ……………………………………5分 ‎16.证法一：‎ 在△ABC和△DCB中, ‎ ‎∵AB=CD，∠ABC =∠BCD，BC边公用， ‎ ‎∴△ABC≌△DCB. ………………………………1分 ‎∴AC=DB， ……………………………………2分 且∠ACB =∠DBC. ……………………………………3分 ‎∴ OB=OC. ……………………………………4分 ‎∴ OA=OD. ………………………………………5分 证法二：‎ ‎……（同证法一）‎ ‎∴△ABC≌△DCB. ………………………………1分 ‎∴∠ACB =∠DBC. ………………………………2分 ‎∴∠ABO=∠DCO. ‎ 又∵∠AOB=∠DOC， …………………………………3分 ‎∴△AOB≌△DOC. ……………………………………4分 ‎∴ OA=OD. ………………………………………5分 ‎ ‎ ‎17.设该班捐献7册和8册图书的人数分别是x、y ……………………………1分 ‎ 依题意,得 ……………………………………3分 ‎ 解得 x=10，y=4 ……………………………………4分 ‎ 答: 该班捐献7册图书的有10人，捐献8册图书的有4人 . 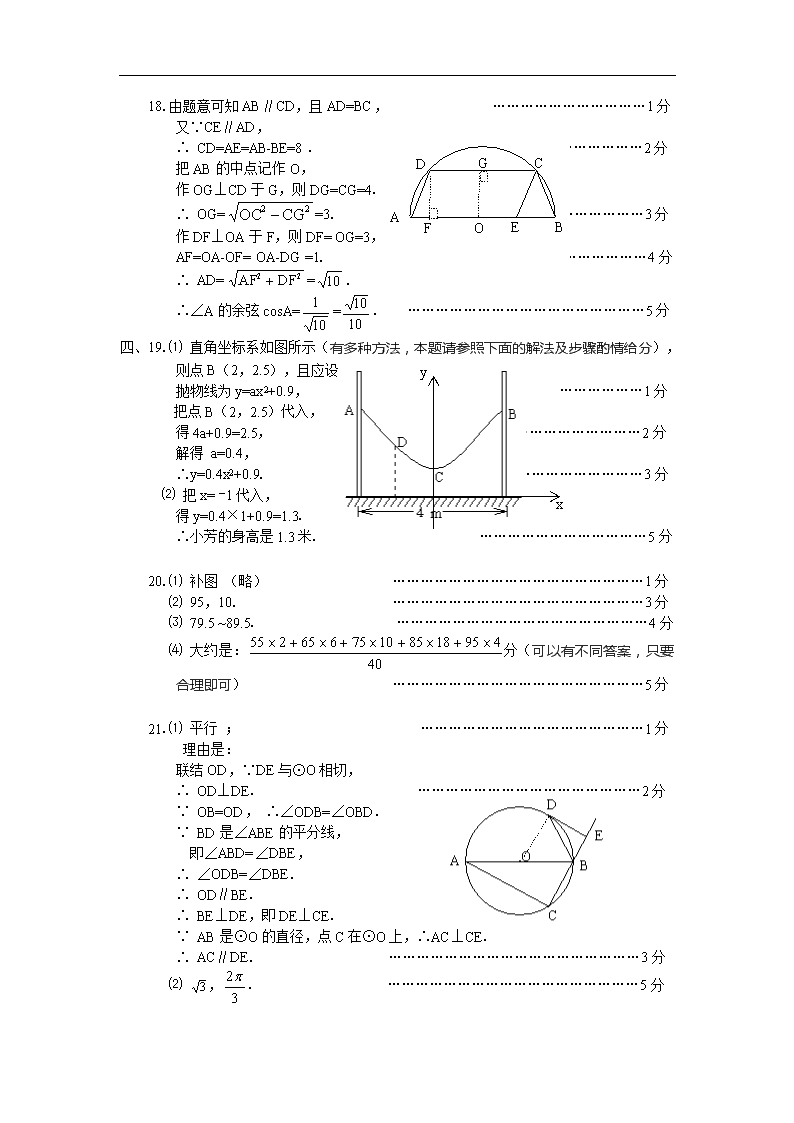…………………5分 ‎18.由题意可知AB∥CD，且AD=BC， ……………………………1分 ‎ 又∵CE∥AD， ‎ O G F ‎∴ CD=AE=AB-BE=8. ………………2分 把AB的中点记作O， 作OG⊥CD于G，则DG=CG=4.‎ ‎∴ OG==3. …………………………………3分 作DF⊥OA于F，则DF= OG=3， AF=OA-OF= OA-DG =1. …………………………4分 ‎∴ AD==. ‎ ‎∴∠A的余弦cosA==. ……………………………………………5分 x y 四、19.⑴ 直角坐标系如图所示（有多种方法，本题请参照下面的解法及步骤酌情给分）， 则点B（2，2.5），且应设 抛物线为y=ax2+0.9， ………………1分 ‎ 把点B（2，2.5）代入， 得‎4a+0.9=2.5， ………………………2分 解得 a=0.4，‎ ‎∴y=0.4x2+0.9. …………………………3分 ‎⑵ 把x= -1代入， 得y=0.4×1+0.9=1.3.‎ ‎∴小芳的身高是‎1.3米. ………………………………5分 ‎ ‎ ‎ 20.⑴ 补图 （略） ………………………………………………1分 ‎ ⑵ 95，10. ………………………………………………3分 ‎ ⑶ 79.5 ~89.5. ………………………………………………4分 ‎ ⑷ 大约是：分（可以有不同答案，只要合理即可） ………………………………………………5分 ‎ ‎ ‎21.⑴ 平行 ； …………………………………………1分 ‎ 理由是：‎ 联结OD，∵DE与⊙O相切，‎ ‎∴ OD⊥DE. …………………………………………2分 ‎ ∵ OB=OD， ∴∠ODB=∠OBD. ‎ ‎ ∵ BD是∠ABE的平分线， 即∠ABD=∠DBE，‎ ‎∴ ∠ODB=∠DBE.‎ ‎∴ OD∥BE.‎ ‎∴ BE⊥DE，即DE⊥CE.‎ ‎∵ AB是⊙O的直径，点C在⊙O上，∴AC⊥CE.‎ ‎∴ AC∥DE. ………………………………………………3分 ‎ ⑵ ，. ………………………………………………5分 ‎22.说明：画出1解给1分，画出2解给2分，画出3解给4分 下面各图供参考：‎ ‎ ‎ 五、23.⑴ 画图基本准确. ………………………………………………1分 B＇‎ ‎ 点A（2，0）、点B＇(3，2) . ………………………3分 ‎⑵ 把点A、点B＇的坐标分别代入y =kx+b，‎ M ‎ 得 ‎ 解得k=2，b= -4.‎ ‎∴直线AB＇表示的函数关系式是y =2x-4 . ………………4分 ‎⑶ ∵△ABB＇为等腰直角三角形，直角边AB==， ‎ ‎∴ S△ABB＇==. ……………………………………5分 在y =+1中，当x=1时，y=0.5. ‎ 即直线x=1与AB交于点M（1，0.5）.‎ 又∵点A和B到CM的距离之和显然为2，‎ ‎∴ S△ABC=CM×2= |a-0.5|=. …………………………………6分 解得，a=3，或-2. …………………………………8分 ‎24.⑴ 证明：∵AC平分∠BAD，‎ ‎∴∠BAC=∠DAC.‎ 又∵∠D =∠B=Rt∠，AC公用，‎ ‎ ∴△ABC≌△ADC.‎ ‎ ∴ BC=CD. …………………………………………1分 ‎ ⑵ 一定相等 . ………………………………………………2分 证明：如图2，不妨设∠B为锐角，作CE⊥AB于E，则点E必在线段AB上 E F ‎ ∵∠B和∠D互为补角，‎ ‎∴∠D是钝角，作CF⊥AD于F， 则点F必在线段AD的延长线上.‎ ‎∴∠CDF与∠ADC互补.‎ ‎∴∠B=∠CDF.‎ 又∵AC是∠BAD的平分线， ∴ CE=CF.‎ ‎∴Rt△BCE≌Rt△DCF ‎∴ BC=CD. ………………………………………………4分 ‎⑶ AB+AD=AC. ………………………………………………5分 ‎ 理由是：图2中，由已知条件，易知AE=AF，BE=DF.‎ ‎∴AB+AD=（AE+BE）+（AF-DF）=AE+AF=2AE.‎ 当∠BAD=60°时，∠CAE=30°，AE=AC.‎ ‎∴AB+AD=2AE=AC. ………………………………………………7分 A D E C B F ‎25. ⑴ (，k -) . …………………………………………1分 ‎⑵ 当m=2，k= -4时，‎ 点C（0，-4），‎ 直线DE为x=3 .‎ 再由 ‎ 代①入②，得x2-10x-24=0，‎ ‎ 解得，x1= -2，x2= 12.‎ ‎∴点A（-2，0）、点E（3，5）. …………………………2分 设抛物线与x轴的另一交点是B，DE与x轴相交于点F（3，0）， ‎ ‎∵CF=AF=EF=BF=5，且△ABE是等腰直角三角形.‎ ‎∴点A、B、C、E都在⊙F上，∠ACE=∠ABE=45°. ………………………4分 ‎⑶ 当m=k＞0时，‎ 由x+m= ，‎ 得x1=0，x2= ‎3m+4＞0. ‎ A E G P1‎ D(P2)‎ ‎∴点A（0，m）. …………………………………5分 显然，经过点A且平行于x轴的直线 与抛物线的另一交点即为点P1（‎3m，m）.‎ ‎ 又∵由题意，点P2只能有一解，‎ 再结合抛物线的对称性，可知点P2只能 重合于点D.‎ 设DE与AP1交于点G，‎ 由DG=AG，即m -（k -）=，得m=. ………………6分 ‎ ∴点P1（8，）、点P2（4，-）. …………………………………8分