2020年广东东莞市莞城街道东莞中学初三一模数学试卷（详解 18页

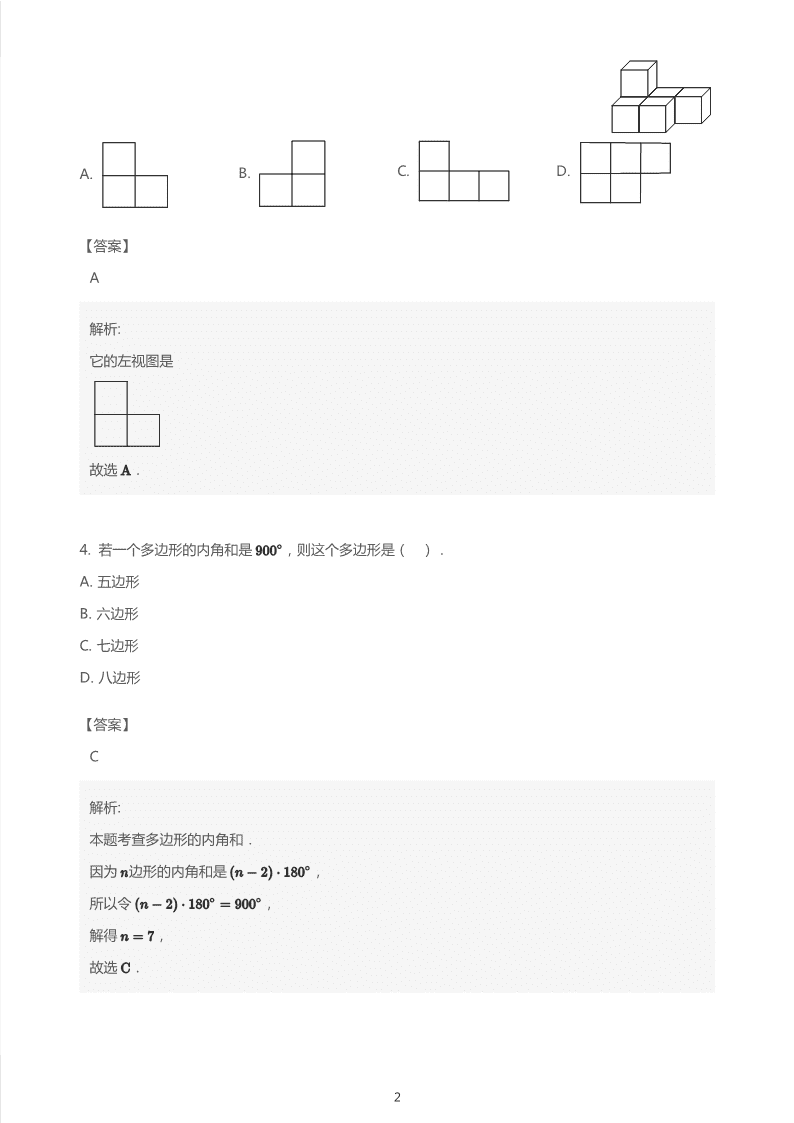
1 2019-2020学年度***学校11月月考卷 考试范围：xxx 考试时间：xxx分钟 命题人：xxx 注意事项: 1. 答题前填写好自己的姓名、班级、考号等信息； 2. 请将答案正确填写在答题卡上。 一、标题 A. B. C. D. 1. 的倒数是（ ）． 【答案】 C 解析: ∵ ， ∴ 的倒数为 ． 故选 ． A. B. C. D. 2. 据民政部网站消息截至 年底，我国 岁以上老年人口已经达到 亿人．其中 亿用科学记 数法表示为（ ）． 【答案】 B 解析: 将 亿用科学记数法表示为 ． 故选 ． 3. 如图是由几个相同的小正方体堆砌成的几何体，它的左视图是（ ）． 2 A. B. C. D. 【答案】 A 解析: 它的左视图是 故选 ． 4. 若一个多边形的内角和是 ，则这个多边形是（ ）． A. 五边形 B. 六边形 C. 七边形 D. 八边形 【答案】 C 解析: 本题考查多边形的内角和． 因为 边形的内角和是 ， 所以令 ， 解得 ， 故选 ． 3 5. 下列图形中，是轴对称图形但不是中心对称图形的是（ ）． A. 等边三角形 B. 正六边形 C. 正方形 D. 圆 【答案】 A 6. 不等式组 的解为（ ）． A. B. C. D. 或 【答案】 C 解析: ， 解①得 ， 解②得 ， ∴ ． 故选 ． ① ② 7. 如图，已知直线 ，一块含 角的直角三角板如图所示放置， ，则 等于（ ）． A. B. 4 C. D. 【答案】 A 解析: 如图所示，作直线 ，则 ， ∴ ， ， ． 选 ． 8. 关于 的一元二次方程 的常数项是 ，则（ ）． A. B. C. 或 D. 【答案】 D 解析: ∵常数项为 ， ∴ 解得 ， 又∵是一元二次方程， ∴ ，所以 ． 故选 ． 5 9. 在 中， ， ，则 的值为（ ）． A. B. C. D. 【答案】 B 解析: ∵ ， ∴ ， ∴ ， ∵ ， ∴ ， ∴ ， ∴ ， 故选 ． 四边形 四边形 10. 如图，在 中， ， ，动点 从点 出发，以 的速度沿 方向运动到点 ，动点 同时从点 出发，以 的速度沿折线AC→CB方向运动到点 ．设 的面积为 ，运动时间为 ，则下列图象能反映 与 之间关系的是（ ）． 6 图 图 A. B. C. D. 【答案】 D 解析: 过点 作 于点 ， ①如图 ，当点 在 上运动时，即 ， 由题意知 、 ， ∵ ， ∴ ， 则 ； ②如图 ，当点 在 上运动时，即 ，此时点 与点 重合， 由题意知 、 ， ∵ ， ∴ ， 则 ． 7 故选： . 11. 若分式 有意义，则 的取值范围为 ． 【答案】 且 解析: 由题意得： ，且 ， 解得： 且 ， 故答案为 且 ． 12. 同时抛掷两枚硬币，恰好均为正面向上的概率是 ． 【答案】 解析: 画树状图为： 正 正正 反反 反 共有 种等可能的结果数，其中两枚硬币全部正面向上的结果数为 ， ∴恰好均为正面向上的概率是 ． 故答案为： ． 13. 分解因式： ． 【答案】 解析: 8 原式 ． 故答案为： ． 14. 如图， 的弦 与半径 交于点 ， ， ，则 的度数为 ． 【答案】 解析: ∵ ， ∴ ， ∵ ， ∴ ， ∵ 和 对的弧都是 ， ∴ ， ∴ ， ∵ ， ∴ ， ∴ ， ∴ ． 15. 已知 ，则 ． 【答案】 解析: 9 ∵ ， ∴ ， 解得 ， ∴ ． 16. 如图， 中， ， ，在以 的中点 为坐标原点， 所在直线 为 轴建立的平面直角坐标系中，将 绕点 顺时针旋转，使点 旋转至 轴正半轴上的 处，则 图中阴影部分面积为 ． 【答案】 解析: ∵ ， ， ∴ 是等腰直角三角形， ∴ ， ∵ 绕点 顺时针旋转点 在 处， ∴ ， ∴ ， ∴ ， ∴ ， 即旋转角为 ， 阴影 扇形 扇形 扇形 扇形 10 ． 故答案为 ． 17. 将一些形状相同的小五角星如下图所示的规律摆放，据此规律，第 个图形有 个五角星． ☆ ☆ ☆ 第 个图形 ☆ ☆ ☆☆ ☆☆☆ ☆ 第 个图形 ☆ ☆ ☆ ☆☆ ☆ ☆☆ 第 个图形 ☆☆☆ ☆☆ ☆ ☆ ☆☆ ☆ ☆ ☆☆ ☆ ☆☆ 第 个图形 ☆☆☆☆ ☆☆ ☆ ☆☆ ☆ ☆☆☆☆ ☆ 【答案】 解析: 第 个图形中小五角星的个数为 ； 第 个图形中小五角星的个数为 ； 第 个图形中小五角星的个数为 ； 第 个图形中小五角星的个数为 ； 则知第 个图形中小五角星的个数为 ； 故第 个图形中小五角星的个数为 个． 故答案为： ． 18. 计算： ． 【答案】 ． 解析: 原式 ． 19. 11 先化简，再求值： ，其中 ． 【答案】 ． 解析: ． 当 时，原式 ． 故答案为： ． （ 1 ） （ 2 ） 20. （ 1 ） 如图， 中， ， ．点 在边 上，且点 到边 和边 的距离 相等． 用直尺和圆规作出点 （不写作法，保留作图痕迹，在图上标注出点 ）． 求点 到边 的距离． 【答案】 （ 1 ） （ 2 ） 画图见解析． ． 解析: 作 的角平分线（或 的垂直平分线）与 的交点即为点 ． 如图： 12 （ 2 ）∵ ， 是 角平分线， ∴ ，垂足为 ， ∵ ， ∴ ， ∵ ，在 中， ∴根据勾股定理求得 ， 设点 到 的距离为 ，则 ，解得 ， 所以点 到边 的距离为 ． （ 1 ） （ 2 ） （ 3 ） 21. 某校积极开展“阳光体育”活动，并开设了跳绳、足球、篮球、跑步四种运动项目，为了解学生最 喜爱哪一种项目，随机抽取了部分学生进行调查，并绘制了如下的条形统计图和扇形统计图（部分信息 未给出）． 跳绳足球 篮球 跑步项目 人数 某校各项运动项目最喜爱 的人数条形统计图 篮球 跑步 足球 跳绳 某校各项运动项目最喜爱 的人数扇形统计图 求本次被调查的学生人数． 补全条形统计图． 该校共有 名学生，请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少? 【答案】 （ 1 ） （ 2 ） ． 画图见解析． 13 （ 1 ） （ 2 ） （ 3 ） （ 3 ） 人． 解析: 观察条形统计图与扇形统计图知：喜欢跳绳的有 人，占 ， 故总人数有 人． 喜欢足球的有 人， 喜欢跑步的有 人， 故条形统计图补充为： 跳绳足球 篮球 跑步项目 人数 某校各项运动项目最喜爱 的人数条形统计图 全校最喜爱篮球的人数比最喜爱足球的人数多 人． （ 1 ） （ 2 ） 22. （ 1 ） 如图，把矩形纸片 沿 折叠后，使得点 落在点 的位置上，点 恰好落在边 上的点 处，连接 ． 求证： 是等腰三角形． 若 ， ，求 的长度． 【答案】 （ 1 ） （ 2 ） 证明见解析． 的长为 ． 解析: ∵四边形 是长方形， 14 （ 2 ） ∴ ， ∴ ， ∵长方形纸片 沿 翻折， ∴ ， ∴ ， ∴ ， ∴ 是等腰三角形． ∵长方形纸片 沿 翻折， ∴ ， ， ，设 的长为 ， ∵ ， ∴ ， 在 中， ，解得 ， ∴ 的长为 ． （ 1 ） （ 2 ） 23. （ 1 ） 六一前夕，某幼儿园园长到厂家选购 、 两种品牌的儿童服装，每套 品牌服装进价比 品牌服 装每套进价多 元，用 元购进 种服装数量是用 元购进 种服装数量的 倍． 求 、 两种品牌服装每套进价分别为多少元？ 该服装 品牌每套售价为 元， 品牌每套售价为 元，服装店老板决定，购进 品牌服装 的数量比购进 品牌服装的数量的 倍还多 套，两种服装全部售出后，可使总的获利超过 元，则 最少购进 品牌的服装多少套？ 【答案】 （ 1 ） （ 2 ） 元， 元 套 解析: 设 品牌服装每套进价为 元，则 品牌服装每套进价为 元，由题意得： ， 解得 ． 经检验： 是原分式方程的解， ． 15 （ 2 ） 答： 、 两种品牌服装每套进价分别为 元， 元． 设购进 品牌的服装 套，则购进 品牌服装 套，由题意得： ， 解得 ． 答：至少购进 品牌的服装是 套． （ 1 ） （ 2 ） （ 3 ） 24. （ 1 ） 如图，在⊙ 中，弦 与弦 相交于点 ， 于点 ，过点 的直线与 的延长线交于 点 ， ． 若 ，求证： 是⊙ 的切线． 若 ， ，请用 表示⊙ 的半径． 求证： ． 【答案】 （ 1 ） （ 2 ） （ 3 ） 证明见解析． ． 证明见解析． 解析: ∵ ， ∴ ， ∵ ， ∴ ， 又∵ ， ， ∴ ， 即 ， 16 （ 2 ） （ 3 ） ∴ ， ∵ 是⊙ 的弦， ∴点 在⊙ 上， ∴ 是⊙ 的切线． ∵ ， ∴ ， ∵ ， ， ∴ ， ∵ ， ∴ ， 即 ， 解得 ， 连接 ，设圆的半径为 ，则 ， 在 中， ， 即 ， 解得 ． 连接 ， ∵ ， （已证）， 17 ∴ ， 又∵ ， ∴ ， ∴ ， 即 ， ∴ ， 即 ． （ 1 ） （ 2 ） （ 3 ） 25. （ 1 ） 已知二次函数 经过点 、 ，与 轴交于另一点 ，抛物线的顶点为 ． x y O 求此二次函数解析式． 连接 、 、 ，求证： 是直角三角形． 在对称轴右侧的抛物线上是否存在点 ，使得 为等腰三角形？若存在，求出符合条件的 点 的坐标．若不存在，请说明理由． 【答案】 （ 1 ） （ 2 ） （ 3 ） 证明见解析． 或 ． 解析: ∵二次函数 经过点 、 ， ∴根据题意，得 ， 解得 ， ∴抛物线的解析式为 ． 18 （ 2 ） （ 3 ） 由 得， 点坐标为 ， ∴ ， ， ， ∵ ， ， ∴ ， ∴ 是直角三角形． 存在． 对称轴为直线 ． ①若以 为底边，则 ， 设 点坐标为 ，根据勾股定理可得 ， ， 因此 ， 即 ． 又 点 在抛物线上， ∴ ， 即 ， 解得 ， ，应舍去， ∴ ， ∴ ， 即点 坐标为 ． ②若以 为一腰， ∵点 在对称轴右侧的抛物线上，由抛物线对称性知，点 与点 关于直线 对称， 此时点 坐标为 ． ∴符合条件的点 坐标为 或 ．