- 332.00 KB
- 2024-01-19 发布
绝密★启用前
2017-2018第二学期汪清六中期末考卷
高二文科数学试卷
考试时间:120分钟;命题人:孙成敏
姓名:__________班级:__________
题号
一
二
三
总分
得分
注意事项:
1. 答题前填写好自己的姓名、班级、考号等信息
2. 请将答案正确填写在答题卡上
评卷人
得分
一、单项选择(每小题5分,共计60分)
1、已知集合,,则集合( )
. . . .
2、已知复数,则=( )
A. B. C. D.
3、函数的零点所在的区间是( )
A. B. C. D.
4、如图2所示,程序框图的输出结果是( )
A. 3 B. 4 C. 5 D. 8
5、袋中有五张卡片,其中红色卡片三张,标号分别为1,2,
3;蓝色卡片两张,标号分别为1,2;从以上五张卡片中任取两张,这两张卡片颜色不同且标号之和小于4的概率为( )
A. B. C. D.
6、一个几何体的三视图如上图所示,则该几何体的体积为 ( )
A. B. C. D.
7、点在极坐标系中的坐标为( )
A. B. C. D.
8、将函数y=2sin (2x+)的图像向右平移个周期后,所得图像对应的函数为
A. y=2sin(2x+) B. y=2sin (2x–)
C. y=2sin(2x–) D. y=2sin(2x+)
9、已知向量,若()与平行,则的值为( )
A. B. C. D.
10、在区间上随机选取一个数,则的概率为( )
A. B. C. D.
11、圆的圆心到直线的距离为1,则( ).
A. B. C. D.
12在中,内角的对边分别是 .若,, ,则等于( )
A. B. C. D.
评卷人
得分
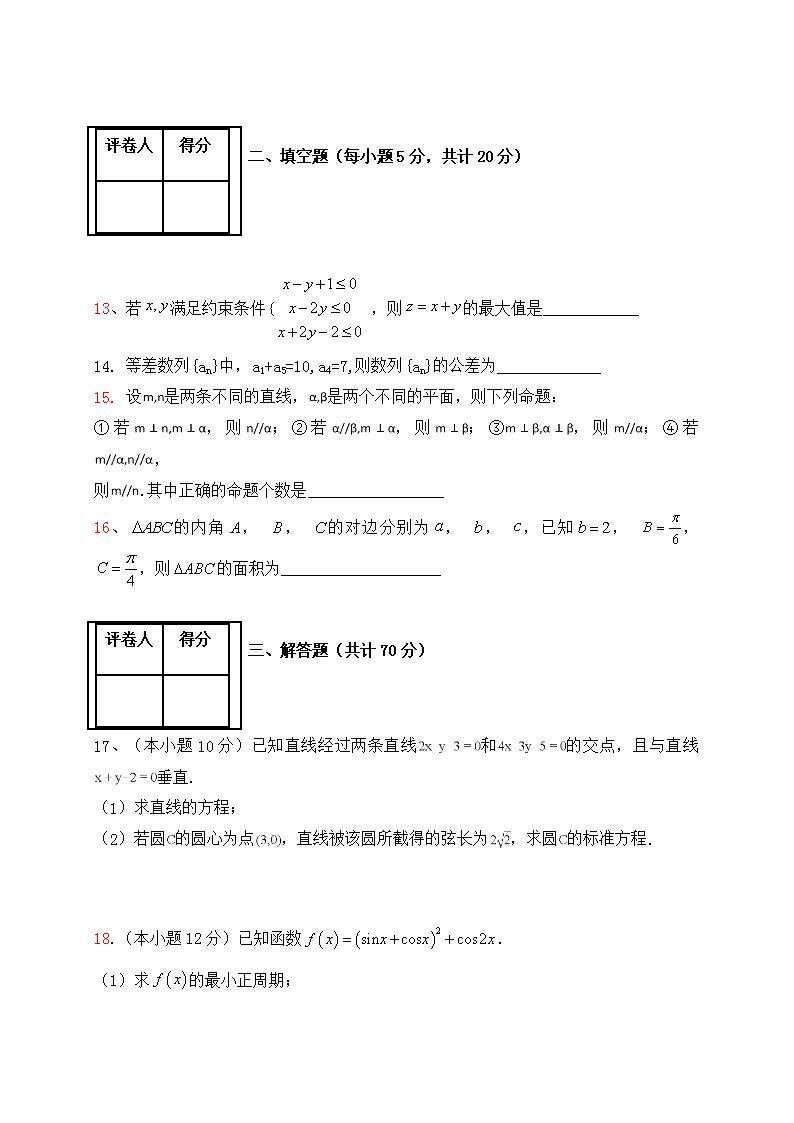
二、填空题(每小题5分,共计20分)
13、若满足约束条件,则的最大值是____________
14. 等差数列{an}中,a1+a5=10,a4=7,则数列{an}的公差为_____________
15. 设是两条不同的直线,是两个不同的平面,则下列命题:
①若,则;②若,则;③,则;④若,
则.其中正确的命题个数是_________________
16、的内角, , 的对边分别为, , ,已知, , ,则的面积为____________________
评卷人
得分
三、解答题(共计70分)
17、(本小题10分)已知直线经过两条直线和的交点,且与直线垂直.
(1)求直线的方程;
(2)若圆的圆心为点,直线被该圆所截得的弦长为,求圆的标准方程.
18.(本小题12分)已知函数.
(1)求的最小正周期;
(2)求在区间上的最大值和最小值.
19.(本小题12分)如图,四棱锥的底面是正方形,侧棱⊥底面是的中点.
(Ⅰ)求证:∥;
(Ⅱ)证明:.
20、(本小题12分)已知{an}为等比数列,a1=1,a4=27;Sn为等差数列{bn}的前n项和,b1=3,S5=35.
(1)求{an}和{bn}的通项公式;
(2)设数列{cn}满足cn=anbn(n∈N),求数列{cn}的前n项和Tn.
21.(本小题12分)在△ABC中,角A为锐角,记角A、B、C所对的边分别为a、b、c,设向量与的夹角为。
(I)求及角A的大小。
(II)若,求△ABC的面积。
22、(本小题12分)已知曲线的参数方程为(为参数)以原点为极点,轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线的极坐标方程;
(Ⅱ)若直线 交曲线于两点,求.
参考答案
一、单项选择
1、【答案】A
3、【答案】C
2、【答案】B
4、【答案】B
5、【答案】C
6、【答案】B
【解析】解:
由已知中的三视图,可得该几何体是:
一个三棱柱挖掉一个三棱锥,所得的组合体,
∵三棱柱的体积V=×22×2=2,
挖去的棱锥体积V=(×22)×1=,
故该几何体的体积为:2﹣=
7、【答案】A
8、【答案】B
9、【答案】A
10、【答案】B
11、【答案】A
12、【答案】D
二、填空题
13、【答案】
14、【答案】d=2
15、【答案】 1
16、【答案】
三、解答题
17.【解】 【答案】(1);(2) .
【解析】试题分析:(1)求出两直线交点,直线的斜率,即可求直线的方程;(2)利用待定系数法求圆的标准方程.
试题解析:(1)由已知得:, 解得两直线交点为,
设直线的斜率为
∵与垂直
∴
∵过点
∴的方程为,即
(2)设圆的半径为,依题意,圆心到直线的距离为,则由垂径定理得
∴
∴圆的标准方程为.
18、【答案】(1);(2)最大值为+1,最小值为0.
试题分析:(1)利用平方和公式,二倍角的正弦函数公式,两角和的正弦函数公式即可化简为f(x)=Asin(ωx+φ)+k的形式,利用周期公式即可得解f(x)最小正周期;
(2)由已知可求,利用正弦函数的图象和性质即可得解f(x)在区间上的最大值和最小值.
试题解析:
(1)∵,
∴f(x)的最小正周期为;
(2)由(1)的计算结果知,f(x)=sin+1.
,
∴,
∴sin(2x+)∈[﹣,1],
∴.
19、【答案】【答案】试题分析:(1)由线线平行得出线面平行;(2)由线面垂直的判定定理证出BD⊥平面PAC,再由线面垂直的性质证得。
试题解析
证:(Ⅰ)连结AC交BD于O,连结OE,
因为四边形ABCD是正方形,所以O为AC中点.
又因为E是PA的中点,所以PC∥OE,
因为PC平面BDE,OE平面BDE,
所以PC∥平面BDE.
(Ⅱ)因为四边形ABCD是正方形,所以BD⊥AC.
因为PA⊥底面ABCD,且BD平面ABCD,所以PA⊥BD.
又AC∩PA=A,AC?平面PAC,PA平面PAC,所以BD⊥平面PAC
又CE平面PAC,所以BD⊥CE.
20、【答案】(1)(2)
试题分析:(1)设等比数列的公比为,由,可得,解得,设等差数列的公差为,由,可得,解得,从而可得结果;(2)由(1)可得,利用“错位相减法”与等比数列的求和公式即可得出.
试题解析:(1)设等比数列{an}的公比为q,∵a1=1,a4=27;∴1×q3=27,解得q=3.
∴.
设等差数列{bn}的公差为d,∵b1=3,S5=35.∴5×3+=35,解得d=2.
∴bn=3+2(n﹣1)=2n+1.
(2)cn=anbn=(2n+1)?3n﹣1.
∴数列{cn}的前n项和Tn=3+5×3+7×32++(2n+1)?3n﹣1.
3Tn=3×3+5×32++(2n﹣1)?3n﹣1+(2n+1)?3n.
∴﹣2Tn=3+2×(3+32++3n﹣1)﹣(2n+1)?3n=3+﹣(2n+1)?3n.
∴Tn=n?3n.
21、【答案】(1),
(2)
试题分析:解(1)由已知得
又
∴
(2)由余弦定理
22、【答案】(1)(2)
试题分析:(Ⅰ)将曲线的参数方程消去参数即可得到普通方程,再将将代入普通方程可得极坐标方程为;(Ⅱ)根据条件可求得直线的直角坐标方程为,由圆的弦长的求法可得弦长。
试题解析:
(Ⅰ)∵曲线的参数方程为(为参数)
∴曲线的普通方程为
曲线表示以为圆心,为半径的圆.
将代入并化简得:
即曲线的极坐标方程为.
(Ⅱ)∵,
∴,
可得直线的直角坐标方程为;
∴圆心到直线的距离为
∴弦长为.