- 503.25 KB
- 2024-01-07 发布
§8.3
直线、平面平行的判定与性质
高考数学
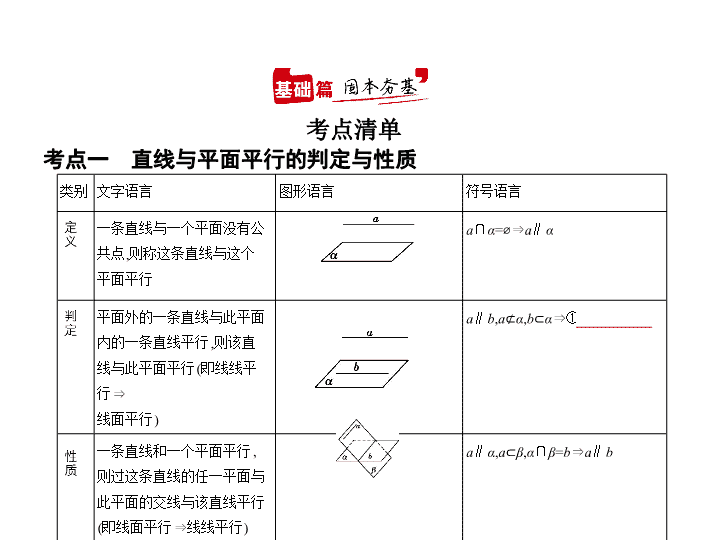
考点一 直线与平面平行的判定与性质
类别
文字语言
图形语言
符号语言
一条直线与一个平面没有公共点,则称这条直线与这个平面平行
a
∩
α
=
⌀⇒
a
∥
α
平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行(即线线平行
⇒
线面平行)
a
∥
b
,
a
⊄
α
,
b
⊂
α
⇒
①
a
∥
α
一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(即线面平行
⇒
线线平行)
a
∥
α
,
a
⊂
β
,
α
∩
β
=
b
⇒
a
∥
b
考点清单
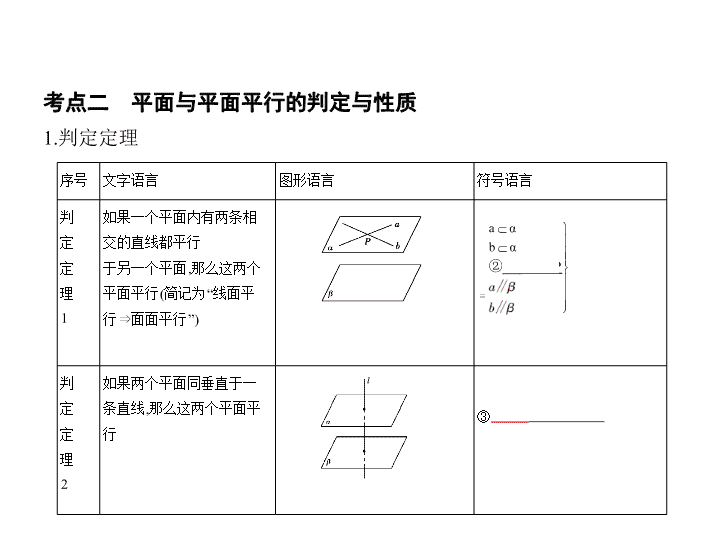
考点二 平面与平面平行的判定与性质
1.判定定理
序号
文字语言
图形语言
符号语言
判
定
定
理
1
如果一个平面内有两条相交的直线都平行
于另一个平面,那么这两个平面平行(简记为“线面平行
⇒
面面平行”)
⇒
α
∥
β
判
定
定
理
2
如果两个平面同垂直于一条直线,那么这两个平面平行
③
⇒
α
∥
β
判定定理3
平行于同一个平面的
两个平面平行
④
2.性质定理
序号
文字语言
图形语言
符号语言
性质
定理1
如果两个平面平行,那么在一个平面内的所有直线都平行于另一个平面
α
∥
β
且
a
⊂
α
⇒
a
∥
β
性质
定理2
如果两个平行平面同时和第三个平面相交,那么它们的交线平行(简记为“面面平行
⇒
线线平行”)
α
∥
β
且
γ
∩
α
=
a
且
γ
∩
β
=
b
⇒
a
∥
b
性质定理3
如果两个平行平面中有一个垂直于一条直线,那么另一个平面也垂直于这条直线
α
∥
β
且
l
⊥
α
⇒
l
⊥
β
知识拓展
线线平行、线面平行、面面平行的相互转化
利用线线平行、线面平行、面面平行的相互转化,解决平行关系的判定时,
一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平
行”,再到“面面平行”;而应用性质定理时,其顺序正好相反.在实际应用
中,判定定理和性质定理一般要相互结合,灵活运用.
考法一
直线与平面、平面与平面平行的证明方法
知能拓展
例1
正方形
ABCD
与正方形
ABEF
所在平面相交于
AB
,在
AE
、
BD
上各有
一点
P
、
Q
,且
AP
=
DQ
.求证:
PQ
∥平面
BCE
.
解题导引
证法一:
证法二:
证明
证法一:如图所示,作
PM
∥
AB
交
BE
于
M
,作
QN
∥
AB
交
BC
于
N
,连接
MN
.
∵正方形
ABCD
和正方形
ABEF
有公共边
AB
,∴
AE
=
BD
.
又
AP
=
DQ
,∴
PE
=
QB
,
∵
PM
∥
AB
∥
QN
,∴
=
=
,
=
,∴
=
,
∴
PM