专题10+对数与对数函数（检测）-2019年高考数学（文）名师揭秘之一轮总复习 24页

‎《2019年高考数学名师揭秘》之一轮总复习（理科）‎ 专题10对数与对数函数 本专题特别注意：‎ ‎1.对数的概念陷阱；‎ ‎2.对数函数的性质陷阱；‎ ‎3.隐含条件陷阱；‎ ‎4.数形结合陷阱；‎ ‎5．参数讨论陷阱；‎ ‎6.根据对数函数图象判断底数大小判断 ‎7.多个函数值比较大小 ‎【学习目标】‎ ‎1．理解对数的概念，掌握指数与对数的相互转化，会运用指数、对数运算法则进行有关运算．‎ ‎2．掌握对数函数的定义、图象和性质及其应用．‎ ‎3．掌握以对数函数为载体的复合函数的有关性质．‎ ‎4．了解指数函数y＝ax与对数函数y＝logax互为反函数(a>0且a≠1)的关系．‎ ‎【知识要点】‎ ‎1．对数的定义 如果ax＝N(a>0且a≠1)，那么数x叫做以a为底N的对数，记作_______________________，其中a叫做对数的底数，N叫做真数．‎ ‎2．几种常见的对数 对数形式 特　　点 记法 一般对数 底数为a(a>0且a≠1)‎ logaN 常用对数 底数为10‎ lg N 自然对数 底数为e ln N N ‎ ‎3.对数的性质(a>0，且a≠1，N>0)‎ N ‎ ‎① ＝________；‎ ‎②logaaN＝________；‎ ‎③换底公式：_____________________________；logab＝，推广logab·logbc·logcd＝logad.‎ logaM＋logaN ‎ ‎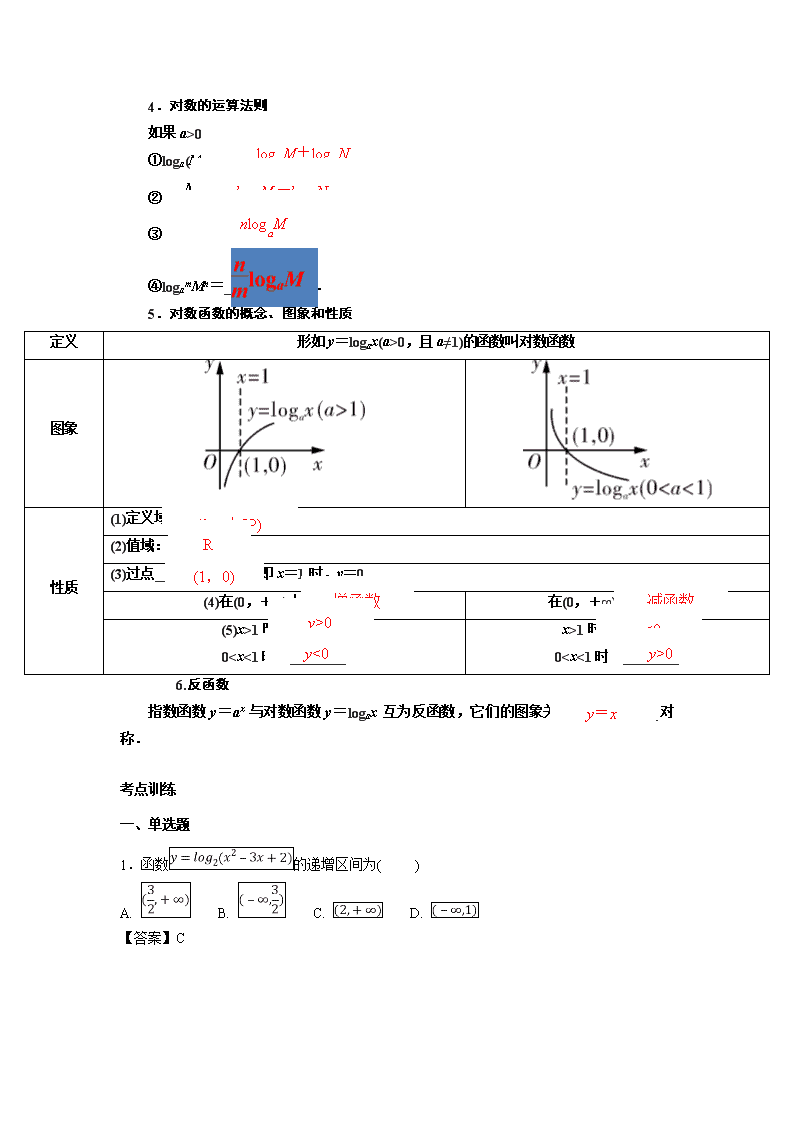4．对数的运算法则 如果a>0且a≠1，M>0，N>0，那么 logaM－logaN ‎ ‎①loga(MN)＝__________________；‎ nlogaM ‎ ‎②loga＝___________________；‎ ‎③logaMn＝_______________；‎ ‎④logamMn＝_____________．‎ ‎5．对数函数的概念、图象和性质 定义 形如y＝logax(a>0，且a≠1)的函数叫对数函数 图象 ‎(0，＋∞) ‎ 性质 R ‎ ‎(1)定义域：_____________‎ ‎(2)值域：________‎ 增函数 ‎ 减函数 ‎ ‎(1，0) ‎ ‎(3)过点_____________，即x＝1时，y＝0‎ y>0 ‎ ‎(4)在(0，＋∞)上是_______‎ y<0 ‎ 在(0，＋∞)上是______‎ y<0 ‎ ‎(5)x>1时，________‎ ‎00 ‎ x>1时，________‎ ‎00，且a≠1)的值域为{y|00，且a≠1)的值域为{y|0b>1‎ ‎1>a>b>0‎ 图象 底数大于1时，底数越大图象越靠近坐标轴 底数小于1时，底数越小图象越靠近坐标轴 无论底数是大于1还是小于1，在x>1时都是“底小图高”．‎