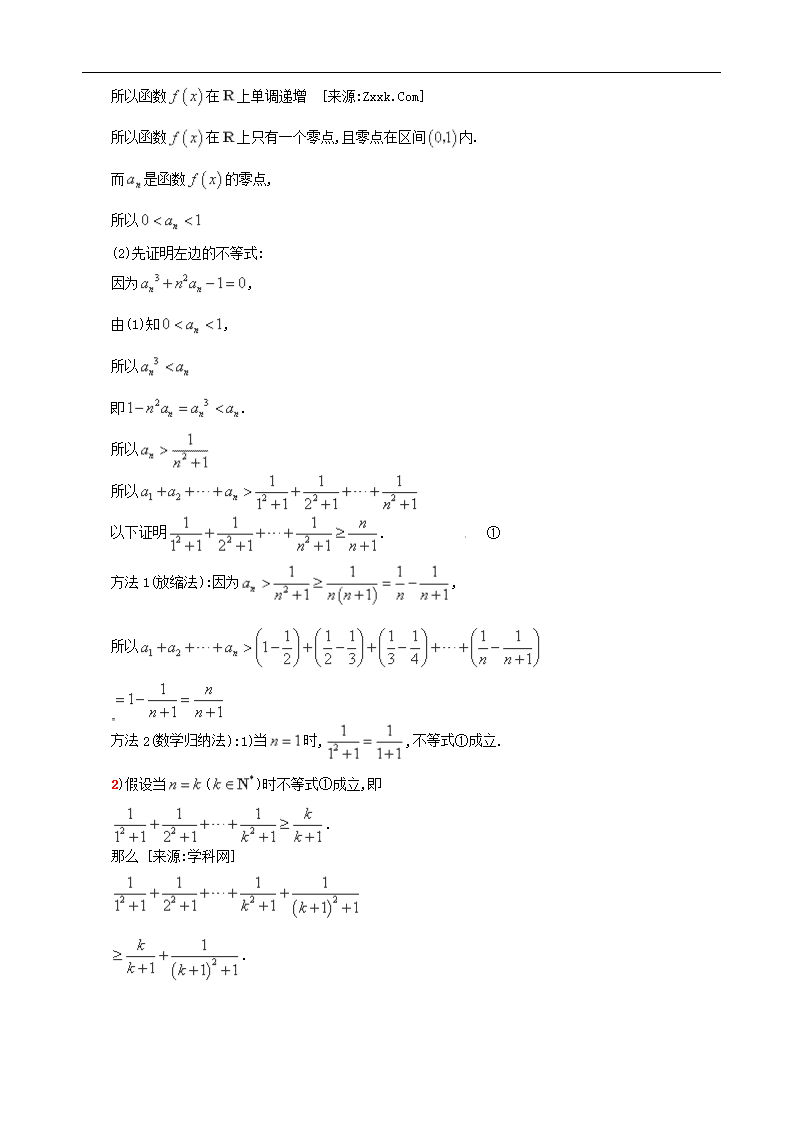广东省2013届高三数学理科试题精选分类汇编16：推理与证明 6页

广东省2013届高三最新理科试题精选（37套含13大市区的二模）分类汇编16：推理与证明 一、选择题 ．（广东省华附、省实、深中、广雅四校2013届高三上学期期末联考数学（理）试题）观察(x2)′=2x,(x4)′=4x3,(cos x)′=-sin x,由归纳推理可得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)= （　　）‎ A．f(x) B．-f(x) C．g(x) D．-g(x)‎ ‎【答案】解:由所给函数及其导数知,偶函数的导函数为奇函数,因此当f(x)是偶函数时,其导函数应为奇函数,故g(-x)=-g(x).选 D． ‎ 二、填空题 ．（2013年广东省佛山市普通高中高三教学质量检测（一）数学（理）试题）观察下列不等式:‎ ‎①;②;③;则第个不等式为_______________.‎ ‎【答案】 ‎ ．（广东省茂名市2013届高三第一次模拟考试数学（理）试题）已知 依此类推,第个等式为_____________.‎ ‎【答案】; ‎ ．（广东省韶关市2013届高三第三次调研考试数学(理科)试题（word版） ）已知正三角形内切圆的半径是高的,把这个结论推广到空间正四面体,类似的结论是____________________.‎ ‎【答案】 ‎ 三、解答题 ．（广东省广州市2013届高三4月综合测试（二）数学理试题（WORD版））设是函数的零点.‎ ‎(1)证明:;‎ ‎(2)证明:.‎ ‎【答案】(本小题主要考查函数的零点、函数的导数和不等式的证明等基础知识,考查运算求解能力和推理论证能力等,本小题满分14分) ‎ 证明:(1)因为,,且在上的图像是一条连续曲线, ‎ 所以函数在内有零点 ‎ 因为, ‎ 所以函数在上单调递增 [来源:Zxxk.Com]‎ 所以函数在上只有一个零点,且零点在区间内. ‎ 而是函数的零点, ‎ 所以 ‎ ‎(2)先证明左边的不等式: ‎ 因为, ‎ 由(1)知, ‎ 所以 ‎ 即. ‎ 所以 ‎ 所以 ‎ 以下证明. ① ‎ 方法1(放缩法):因为, ‎ 所以 ‎ ‎ ‎ 方法2(数学归纳法):1)当时,,不等式①成立. ‎ ‎2)假设当()时不等式①成立,即 ‎ ‎. ‎ 那么 [来源:学科网]‎ ‎ ‎ ‎. ‎ 以下证明. ② ‎ 即证. ‎ 即证. ‎ 由于上式显然成立,所以不等式②成立. ‎ 即当时不等式①也成立. ‎ 根据1)和2),可知不等式①对任何都成立. ‎ 所以 ‎ 再证明右边的不等式: ‎ 当时,. ‎ 由于,, ‎ 所以 ‎ 由(1)知,且,所以 ‎ 因为当时,, ‎ 所以当时, ‎ ‎. ‎ 所以当时,都有. ‎ 综上所述, ‎ ．（广东省广州市2013届高三调研测试数学（理）试题）若函数对任意的实数,,均有,则称函数是区间上的“平缓函数”. ‎ ‎(1) 判断和是不是实数集R上的“平缓函数”,并说明理由;‎ ‎(2) 若数列对所有的正整数都有 ,设, ‎ 求证: .‎ ‎【答案】(本小题主要考查函数、绝对值不等式等基础知识,考查函数与方程、分类与整合、化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力、创新意识) ‎ ‎(1) 解:是R上的“平缓函数”,但不是区间R的“平缓函数”; ‎ 设,则,则是实数集R上的增函数, ‎ 不妨设,则,即, ‎ 则. ① ‎ 又也是R上的增函数,则, ‎ 即, ② ‎ 由①、②得 . ‎ 因此,,对都成立 ‎ 当时,同理有成立 [来源:学*科*网Z*X*X*K]‎ 又当时,不等式, ‎ 故对任意的实数,R,均有. ‎ 因此 是R上的“平缓函数” ‎ 由于 ‎ 取,,则, [来源:Zxxk.Com]‎ 因此, 不是区间R的“平缓函数” ‎ ‎(2)证明:由(1)得:是R上的“平缓函数”, ‎ 则, 所以 ‎ 而, [来源:学科网]‎ ‎∴ ‎ ‎∵, [来源:学+科+网] ‎ ‎∴ ‎ ‎∴ ‎ ‎ ‎ ‎ ‎ ‎[来源:学§科§网]‎ ．（广东省珠海一中等六校2013届高三第二次联考数学（理）试题）设函数.‎ ‎(1)证明:存在唯一实数,使;‎ ‎(2)定义数列 ‎ ‎① 对(1)中的,求证:对任意正整数都有;‎ ‎② 当时,若,证明:对任意都有 ‎[来源:Z§xx§k.Com]‎ ‎【答案】(1)解:有令 ‎ 由所以有且只有一个实数,使; ‎ ‎(1) (Ⅰ)(数学归纳法)先证: ‎ 证明: ① ; ‎ ‎② 假设 由递减性得: ‎ 即 [来源:学科网ZXXK]‎ 又 ‎ 所以时命题成立 所以对成立 ‎ ‎(2)(Ⅱ)解:当时, 为减函数,且 ‎ ‎ ‎ 由 [来源:学科网ZXXK]‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎[来源:学科网]‎