- 2.83 MB
- 2023-11-13 发布
2013 年上海市奉贤区中考数学一模试卷
(满分 150 分,考试时间 100 分钟) 2013.01
一、选择题:(本大题共 6 题,每题 4 分,满分 24 分)
[每小题只有一个正确选项,在答题纸的相应题号的选项上用 2 B 铅笔填涂]
1.把抛物线 2xy 向右平移 2 个单位后得到的抛物线是(▲)
A. 2)2( xy ; B. 2)2( xy ; C. 22 xy ; D. 22 xy ;
2.在 Rt ABC 中, 90C ,a,b,c 分别是 ,,A B C 的对边,下列等式中正确的是(▲)
A.sin bA c ; B. cos cB a ; C. tan aA b ; D. cot bB a ;
3.等腰直角三角形的腰长为 2 ,该三角形的重心到斜边的距离为(▲)
A.
3
22 ; B.
3
2 ; C.
3
2 ; D.
3
1 ;
4.若两个相似三角形的面积之比为 1:4,则它们的最大边的比是(▲)
A. 1:2; B. 1:4; C. 1:5; D. 1:16;
5.如图,已知直线 a∥b∥c,直线 m、n 与 a、b、c 分别交于点 A、C、E、B、
D、F,AC=4,CE=6,BD=3,则 BF=(▲)
A. 7; B. 7.5; C. 8; D.8.5;
6.在两个圆中有两条相等的弦,则下列说法正确的是(▲)
A.这两条弦所对的弦心距相等; B.这两条弦所对的圆心角相等;
C.这两条弦所对的弧相等; D.这两条弦都被垂直于弦的半径平分;
二、填空题:(本大题共 12 题,每题 4 分,满分 48 分)
【请将结果直接填入答题纸的相应位置】
7. 二次函数 32 xy 图像的顶点坐标是 ▲ ;
8.抛物线 2y ax )0( a 的图像一定经过 ▲ 象限;
9.抛物线 )5)(1( xxy 的对称轴是:直线 ▲ ;
10.已知抛物线 322 xxy ,它的图像在对称轴 ▲ (填“左侧”或“右侧”)的部分是下降的;
11.已知 D 、E 分别是 ABC 的边 AB 、AC 的延长线上的点, 若
3
7AB
AD ,则
AE
AC 的值是 ▲ 时,DE
∥ BC ;
a
b
c
A B
C D
E F
m n
第 5 题
A l1
第 20 题
F
G
B C l2
12.已知线段 3a cm , 6c cm ,若线段c 是线段 a 、b 的比例中项,则b = ▲ cm;
13.已知三角形三边长为 3、4、5,则最小角的正弦是 ▲ ;
14.在高为 100 米的楼顶测得地面上某十字路口的俯角为 ,那么楼底到这十字路口
的水平距离是▲ 米;(用含角 的三角比的代数式表示)
15.在 RtΔ ABC 中,∠C=90º,tanA=
2
1 ,那么 cotB 的值为 ▲ ;
16.若⊙O 的一条弦长为 24,弦心距为 5,则⊙O 的直径长为 ▲ ;
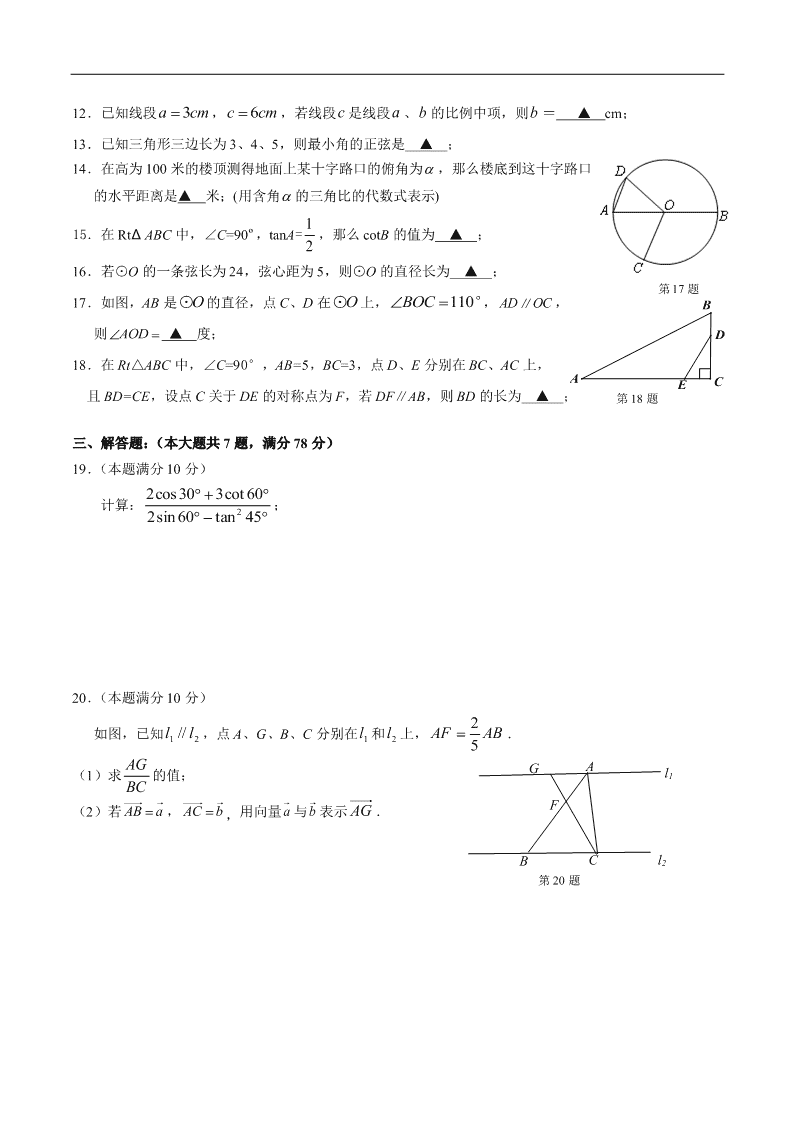
17.如图,AB 是 O⊙ 的直径,点 C、D 在 上, 110BOC°, AD OC∥ ,
则 AOD ▲ 度;
18.在 Rt△ABC 中,∠C=90°,AB=5,BC=3,点 D、E 分别在 BC、AC 上,
且 BD=CE,设点 C 关于 DE 的对称点为 F,若 DF∥AB,则 BD 的长为 ▲ ;
三、解答题:(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
计算:
45tan60sin2
60cot330cos2
2 ;
20.(本题满分 10 分)
如图,已知 21 // ll ,点 A、G、B、C 分别在 1l 和 2l 上, ABAF 5
2 .
(1)求
BC
AG 的值;
(2)若 AB a , AC b ,用向量 a 与b 表示 AG .
A C
B
D
E
第 18 题
第 17 题
21.(本题满分 10 分,每小题满分各 5 分)
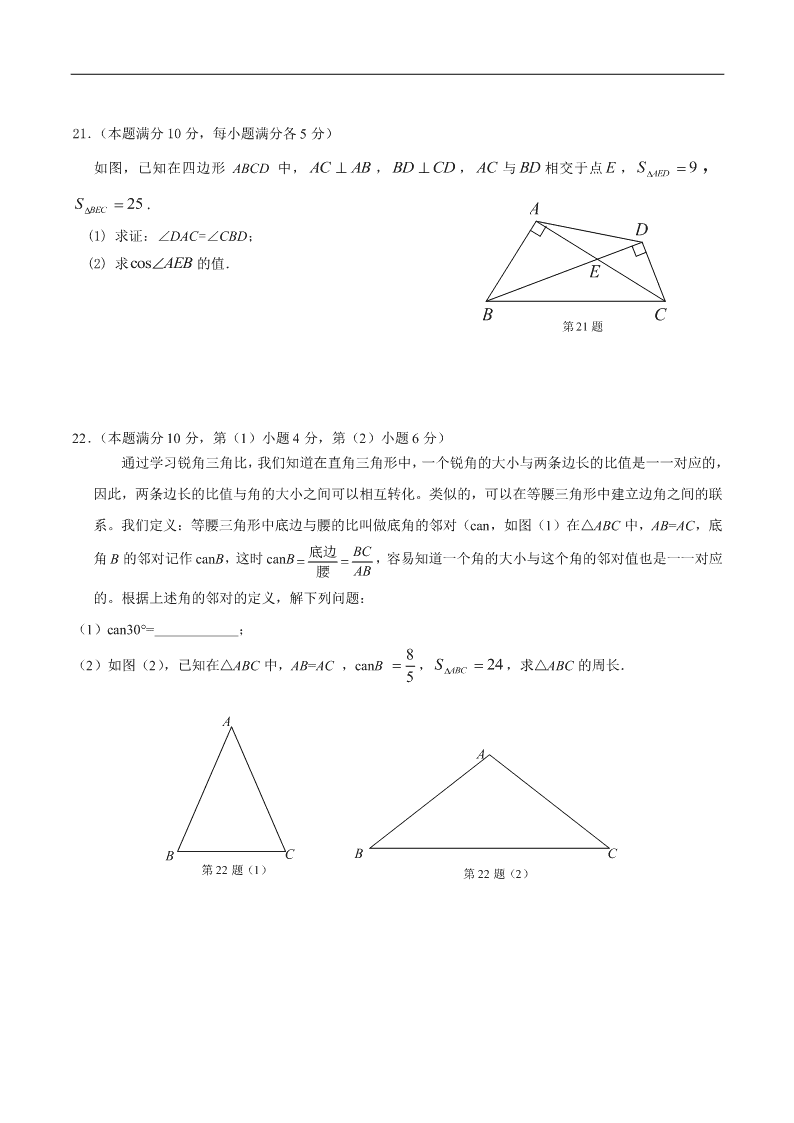
如图,已知在四边形 ABCD 中, ABAC , CDBD , AC 与 BD 相交于点 E , 9AEDS ,
25BECS .
(1) 求证:∠DAC=∠CBD;
(2) 求 AEBcos 的值.
22.(本题满分 10 分,第(1)小题 4 分,第(2)小题 6 分)
通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,
因此,两条边长的比值与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联
系。我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can,如图(1)在△ABC 中,AB=AC,底
角 B 的邻对记作 canB,这时 canB BC
AB底边
腰
,容易知道一个角的大小与这个角的邻对值也是一一对应
的。根据上述角的邻对的定义,解下列问题:
(1)can30°= ;
(2)如图(2),已知在△ABC 中,AB=AC ,canB
5
8 , 24ABCS ,求△ABC 的周长.
第 21 题
E
D
CB
A
B
A
A
第 22 题(2)
B C C
第 22 题(1)
B
第 23 题
D
E
F C B
A
23.(本题满分 12 分,每小题满分各 6 分)
如图,已知在 ABCRt 中, 90ACB , ABCD 于 D ,
E 是 AC 的中点, DE 的延长线与 BC 的延长线交于点 F .
(1)求证:△FDC∽△FBD;
(2)求证:
BC
AC
BF
DF .
24.(本题满分 12 分,每小题 4 分)
如图,已知直线 xy 与二次函数 2y x bx c 的图像交于点 A、O,(O 是坐标原点),点 P 为二次函数图
像的顶点,OA=32,AP 的中点为 B.
(1)求二次函数的解析式;
(2)求线段 OB 的长;
(3)若射线 OB 上存在点 Q,使得△AOQ 与△AOP 相似,
求点 Q 的坐标.
第 24 题
O
A
x
y
P
B
25.(本题满分 14 分,第(1)小题 4 分,第(2)小题 5 分,第(3)小题 5 分)
如图(1),已知∠MON=90°,点 P 为射线 ON 上一点,且 OP=4,B、C 为射线 OM 和 ON 上的两个动点
( OPOC ),过点 P 作 PA⊥BC,垂足为点 A,且 PA=2,联结 BP .
(1)若 1
2
PAC
ABOP
S
S
四边形
时,求 tan∠BPO 的值;
(2)设 ,, yBC
ABxPC 求 y 与 x 之间的函数解析式,并写出定义域;
(3)如图(2),过点 A 作 BP 的垂线,垂足为点 H,交射线 ON 于点 Q,点 B、C 在射线 OM 和 ON 上运动
时,探索线段 OQ 的长是否发生变化?若不发生变化,求出它的值。若发生变化,试用含 x 的代数式表
示 OQ 的长.
P C
第 25 题 (1)
A
B
M
O P C
第 25 题 (2)
A
B
M
O Q
H
N N
2013 年上海市奉贤区中考数学一模试卷
参考答案 201301
一 、选择题:(本大题共 8 题,满分 24 分)
1.A ; 2.C; 3.D; 4.A; 5.B ; 6.D;
二、填空题:(本大题共 12 题,满分 48 分)
7.( 0,3); 8.一、二; 9. 2x ; 10.左侧;
11.
7
3 ; 12.12; 13.
5
3 ; 14. cot100 ;
15.1; 16.26; 17.40; 18.1;
三.(本大题共 7 题,满分 78 分)
19. (本题满分 10 分)
解:原式=
212
32
2
332
32
-------------------------------------------------(每个值得 2 分,共 8 分)
= 33
13
32
---------------------------------------------------------------------(2 分)
20.(本题满分 10 分,4+6)
(1)∵ 21 // ll ∴
BC
AG
BF
AF ------------------------------------------------------------------(2 分)
∵ ABAF 5
2 ∴
3
2BF
AF ∴
3
2BC
AG ---------------------------------------------(2 分)
(2) ∵ AB a , AC b ∴ abBC --------------------------------------------------(3 分)
∵ ∴ AG = baabBC 3
2
3
2)(3
2
3
2 ---------------------(3 分)
21.(本题满分 10 分,每小题满分各 5 分)
(1)∵ ABAC , CDBD ∴∠CAB=∠BDC=90°-------------------------------(1 分)
∵∠AEB=∠DEC ∴△AEB∽△DEC------------------------------------------------(1 分)
∴
CE
BE
DE
AE -----------------------------------------------------------------------------------(1 分)
∵∠AED=∠BEC ∴△AED∽△BEC---------------------------------------------------(1 分)
∴∠DAC=∠CBD-------------------------------------------------------------------------------(1 分)
(2) ∵△AED∽△BEC ∴ 2)( BE
AE
S
S
BEC
AED
---------------------------------------------(2 分)
∵ 9AEDS , 25BECS ∴
5
3BE
AE ----------------------------------------(1 分)
∴RtΔ ABE 中, AEBcos = -----------------------------------------------------------(2 分)
22.(本题满分 10 分,第(1)小题 4 分,第(2)小题 6 分)
(1)can30°= 3 -------------------------------------------------------------------------------------(4 分)
(2)∵在△ABC 中, canB
5
8 ,∴
5
8AB
BC -----------------------------------------------(1 分)
设 kABkBC 5,8
过点 A 作 AH BC 垂足为点 H,
∵AB=AC ∴ kBH 4
∵ 24ABCS ∴ 24482
1 kk 2k ---------------------------------------(2 分)
∴ 28,25 BCACAB ---------------------------------------------------------------------(2 分)
∴△ABC 的周长= 218 .----------------------------------------------------------------------------(1 分)
23.(本题满分 12 分,每小题满分各 6 分)
(1)∵ 90ACB , ABCD
∴∠ACD+∠DCB=∠B=∠DCB=90°
∴∠ACD=∠B--------------------------------------------------------------------------------------------(2 分)
∵ E 是 AC 的中点 ∴DE=EC
∴∠ACD=∠FDC
∴∠FCD=∠B-------------------------------------------------------------------------------------------(2 分)
∴△FDC∽△FBD--------------------------------------------------------------------------------------(2 分)
(2) ∵△FDC∽△FBD ∴
BD
DC
BF
DF ----------------------------------------------------------------(2 分)
∵在 ABCRt 和 DBCRt 中,
BD
DC
BC
ACB tan ------------------------------------------(2 分)
∴
BC
AC
BF
DF -----------------------------------------------------------------------------------------------(2 分)
24.(本题满分 12 分,每小题各 4 分)
H
M
O N
A
B
P CQ E
∵点 A 在直线 xy 上,且 32OA ∴A(3,3) ------------------------------------------------(1 分)
∵ 点 O(0,0) A(3,3)在 2y x bx c 的图像上,
∴
339
0
cb
c
解得:
0
2
c
b
------------------------------------------------------(2 分)
∴二次函数的解析式为 2 2y x x---------------------------------------------------------------------(1 分)
(2)由题意得顶点 P(1,-1) ---------------------------------------------------------------------------(1 分)
∴ 52,2,23 APPOAO
∴ 222 APPOAO ∴∠AOP=90°---------------------------------------------------------(2 分)
∵∠AOP=90°,B 为 AP 的中点 ∴ 5OB ------------------------------------------------(1 分)
(3) ∵∠AOP=90°,B 为 AP 的中点
∴OB=AB ∴∠AOB=∠OAB
若△AOQ 与△AOP
则①△AOP∽△OQA ∴
OA
AP
OQ
AO ∴ 55
9
1 OQ ---------------------------------------(1 分)
②△AOP∽△OAQ ∴
OQ
AP
AO
AO 522 OQ ----------------------------------------------(1 分)
∵B(2,1) ∴ )2,4(),5
9,5
18( 21 QQ -------------------------------------------------------------------(2 分)
即点 Q 的坐标 时,△AOQ 与△AOP 相似。
25.(本题满分 14 分,第(1)小题 4 分,第(2)小题 5 分,第(3)小题 5 分)
(1)∵∠ACP=∠OCB ∠CAP=∠O=90°
∴△CAP∽△COB-------------------------------------(1 分)
∴ 2()PAC
COB
AP
OB
S
S
-------------------------------(1 分)
∵ 1
2
PAC
ABOP
S
S
四边形
∴ 1
3
PAC
COB
S
S
∴ 2 1()3
AP
OB
∵AP=2 ∴ 23OB -------------------------(1 分)
在 Rt△OBP 中, 3tan 2
OBOPB OP -----------------(1 分)
(2)作 AE⊥PC,垂足为 E,---------------------------------------------------------------------(1 分)
易证△PAE∽△PCA ∴
PA
PE
PC
PA
∴ 22 PE x ∴ 4PE x -------------------------------------------------------------------(1 分)
∵∠MON=∠AEC=90° ∴ AE∥OM
∴ AB OE
BC OC ----------------------------------------------------------------------------------(1 分)
∴
44
4
xy x
整理得 2
44
4
xy xx
(x>2) ------------------------------(2 分)
(3)线段 OQ 的长度不会发生变化-----------------------------------------------------------(1 分)
由△PAH∽△PBA 得
PA
PH
PB
PA 即 2PA PH PB------------------------(1 分)
由△PHQ∽△POB 得
PO
PH
PB
PQ 即 PQ PO PH PB ---------------------(1 分)
∴ 2PA PQ PO
∵PA=2 PO=4 ∴PQ=1 ----------------------------------------------------------------(1 分)
∴OQ=3--------------------------------------------------------------------------------------------------(1 分)
即 OQ 的长度等于 3。
浦东新区 2012 学年度第一学期期末质量测试
初三数学试卷 2013.1.17
(测试时间:100 分钟,满分:150 分)
考生注意:
1.本试卷含三个大题,共 25 题,答题时,考生务必按答题要求在答题纸规定的位置作答,在草稿纸、本试
卷上
答题一律无效;
2. 除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤;
3.本次测试可使用科学计算器.
一、选择题:(本大题共 6 题,每题 4 分,满分 24 分)
1.如果延长线段 AB 到C ,使得 1
2BC AB ,那么 :AC AB 等于( )
A .2:1; B .2:3; C .3:1; D.3:2.
2.已知 Rt ABC 中, 90C , A , 2AB ,那么 BC 长( )
. 2sin ; . 2cos ; . 2
sin
; . 2
cos
.
3.如果将抛物线 2yx 向左平移 2 个单位,那么所得到的抛物线表达式为( )
. 2 2yx; . 2 2yx; . 2( 2)yx ; . 2( 2)yx .
4.如果抛物线 2y ax bx c 经过点( 1, 0) 和(3, 0) ,那么对称轴是直线( )
. =0x ; . =1x ; . =2x ; . =3x .
5.如果乙船在甲船的北偏东 40 方向上,丙船在甲船的南偏西 40 方向上,那么丙船在乙船的方向是( )
.北偏东 40 ; .北偏西 40 ; .南偏东 40 ; .南偏西 40 .
6.如图,已知在 ABC 中,边 6BC ,高 3AD ,正方形 EFGH 的顶点 FG、 在边 BC 上,顶点 EH、
分别在边 AB 和 AC 上,那么这个正方形的边长等于( )
.3;
.2.5;
.2;
.2.5.
二、填空题:(本大题共 12 题,,每题 4 分,满分 48 分)
7. 已知线段b 是线段 a 、c 的比例中项,且 a=1、 =2b 那么 =c .
8.计算: 11( ) (2 )22a b a b .
9.如果抛物线 2(2 )y a x 的开口方向向下,那么 a 的取值范围是 .
10.二次函数 2 3yx的图像的最低点坐标是 .
11.在边长为6 的正方形中间挖去一个边长为 (0 6)xx 的小正方形,如果设剩余部分的面积为 y ,那么
关于 x 的函数解析式为 .
12.已知 是锐角, 2 30tan cos ,那么 度.
13.已知从地面进入地下车库的斜坡的坡度为1: 2.4,地下车库的地坪与地面的垂直距离等于5 米,那么此
斜坡的长度等于 米.
14.小明用自制的直角三角形纸板 DEF 测量树 AB 的高度.测量时,使直角边 DF 保持水平状态,其延长
线交 AB 于点G ;使斜边 DE 与点 A 在同一条直线上.测得边 DF 离地面的高度为1.4m,点 D 到 AB 的距
离等于6m (如图所示)。已知 30DF cm , 20EF cm ,那么树 AB 的高度等于 m .
15.如图,将△ ABC 沿射线 BC 方向平移得到△ DEF ,边 DE 与 AC 相交于点G ,如果 3BC cm ,
△ 的面积为 29cm ,△ 的面积等于 24cm ,那么 BE cm .
16.相邻两边长的比值是黄金分割数的矩形,叫做黄金矩形,从外形看,它最具美感. 现在想要制作一张“黄
金矩形”的贺年卡,如果较长的一条边长等于 20 厘米,那么相邻一条边的边长等于 厘米.
17.九年级数学课本上,用“描点法”画二次函数 2y ax bx c 的图像时,列出了如下的表格:
x … 0 1 2 3 4 …
… 3 0 1 0 3 …
那么该二次函数在 5x 时, y .
18.已知在 Rt △ ABC 中, 90A , 5sin 5B , BC a ,点 D 在边 BC 上,将这个三角形沿直线
AD 折叠,点C 恰好落在边 AB 上,那么 BD .(用 a 的代数式表示)
三、解答题:(本大题共 7 题,满分 78 分)
19.(本题满分 10 分,其中第(1)小题 6 分,第(2)小题 4 分)
已知:抛物线 2y x bx c 经过 (3 0)B , 、 (0, 3)C 两点,顶点为 A .
求:(1)抛物线的表达式;
(2)顶点 A 的坐标.
20.(本题满分 10 分,其中第(1)小题 6 分,第(2)小题 4 分)
如图,已知在平行四边形 ABCD中, MN、 分别是边 AD DC、 的中点,设 AB a , AD b .
(1)求向量 MD MN、 (用向量 ab、 表示);
(2)求作向量 MN 在 AB AD、 方向上的分向量.
(不要求写作法,但要指出所作图中表示结论的向量)
21.(本题满分 10 分)
某条道路上通行车辆限速为60 /千米 时,在离道路50 米的点处建一个监测点 P ,道路 AB 段为检测
区(如图). 在△ ABP 中,已知 32PAB, 45PBA,那么车辆通过 AB 段的时间在多少秒以内
时,可认定为超速(精确到 0.1秒)?
(参考数据: 32 0.53sin , 32 0.85cos , 32 0.62tan , 32 1.60cot )
22.(本题满分 10 分)
如图,在平行四边形 ABCD中,点 E 在边 BC 上,连接 AE 并延长,交对角线 BD 于点 F 、 DC 的延
长线于点G ,如果 3
2
BE
EC .求 EF
EG
的值.
23.(本题满分 12 分,每小题各 6 分)
已知:如图,在梯形 ABCD中, AD ∥ BC , AB BC ,点 M 在边 BC 上,且 MDB ADB ,
2BD AD BC.
(1)求证: BM CM ;
(2)作 BE DM ,垂足为点 E ,并交CD 于点 F . 求证: 2AD DM DF DC .
24.(本题满分 12 分,其中第(1)小题 3 分,第(2)小题 4 分,第(3)小题 5 分)
如图,在直角坐标系 xOy 中,二次函数 22 53y x bx 的图像与 x 轴、 y 轴的公共点分别为
(5 0)A 、 、 B ,点C 在这个二次函数的图像上,且横坐标为3 .
(1)求这个二次函数的解析式;
(2)求 BAC 的正切值;
(3)如果点 D 在这个二次函数的图像上,且 45DAC,求点 D 的坐标.
25.(本题满分 14 分,其中第(1)小题 4 分,第(2)、(3)小题各 5 分)
如图,已知在△ ABC 中, =90A , = =3 2AB AC ,经过这个三角形重心的直线 DE ∥ BC ,分别
交边 AB 、 AC 于点 D 和点 E , P 是线段 DE 上的一个动点,过点 P 分别做 PM BC , PF AB ,
PG AC ,垂足分别为点 M 、 F 、G . 设 BM x ,四边形 AFPG 的面积为 y .
(1)求 PM 的长;
(2)求 y 关于 x 的函数解析式,并写出它的定义域;
(3)连接 MF 、 MG ,当△ PMF 与△ PMG 相似时,求 BM 的长.
浦东新区 2012 学年第一学期期末教学质量调研 初中九年级 数学试卷
参考答案及评分标准 2013.1.17
一、选择题:(本大题共 6 题,每题 4 分,满分 24 分)
1.D; 2.A; 3.C; 4.B; 5.D; 6.C.
二、填空题:(本大题共 12 题,每题 4 分,满分 48 分)
7.4; 8. b ; 9. 2a ; 10.(0,-3); 11. 2 36yx ; 12.60;
13.13; 14.5.4; 15.1; 16.10 5 10 (或 12.36); 17.8; 18. 2
3 a .
三、解答题:(本大题共 7 题,满分 78 分)
19.解:(1)∵ 抛物线 2y x b x c 经过 B(3,0)、C(0,3)两点,
∴ 9 3 0 ,
3.
bc
c
………………………………………………… (2 分)
解得 2,
3.
b
c
…………………………………………………………(2 分)
∴ 抛物线的解析式是 2 23y x x .……………………………(2 分)
(2)由 222 3 ( 1) 4y x x x ,…………………………………(2 分)
得顶点 A 的坐标为(1,4). …………………………………………(2 分)
20.解:(1)∵ M 是边 AD 的中点,∴ 11
22MD AD b.……………………(2 分)
∵ 四边形 ABCD 是平行四边形,∴ DC // AB,DC = AB.
∴ DC AB a.……………………………………………………(1 分)
又∵ N 是边 DC 的中点,∴ aDN 2
1 . …………………………(1 分)
∴ 11
22MN MD DN b a .……………………………………(2 分)
(2)作图正确,3 分;结论正确,1 分.
21.解:过点 P 作 PC⊥AB,垂足为点 C.…………………………………………(1 分)
根据题意,可知 PC = 50 米.
在 Rt△PBC 中,∠PCB = 90º,∠B = 45º,
∴ cot 50 cot 45 50BC PC B .……………………………………(3 分)
在 Rt△PAC 中,∠PCA = 90º,∠PAB = 32º,
∴ cot 50 cot32 80AC PC PAB .………………………………(2 分)
∴ AB = AC +BC ≈ 80 +50 = 130(米).…………………………………(1 分)
∵ 130 3600 7.860 1000
(秒),…………………………………………(2 分)
∴ 车辆通过 AB 段的时间在 7.8 秒以内时,可认定为超速.…………(1 分)
22.解:∵ 四边形 ABCD 是平行四边形,
∴ BC // AD,AB // CD,BC = AD.………………………………………(2 分)
∴ EF BE
AF AD , AE BE
GE CE .………………………………………………(2 分)
又∵ 3
2
BE
EC ,∴ 3
5
BE
BC .……………………………………………(2 分)
即得 3
5
BE EF
AD AF, 3
2
AE
GE .∴ 3
8
EF
AE .…………………………(2 分)
∴ 3 3 9
8 2 16
EF AE
AE EG .
即得 9
16
FE
EG .……………………………………………………………(2 分)
23.证明:(1)∵ AB⊥BC,∴ ∠ABC = 90º.
∵ AD // BC,∴ ∠CBD =∠ADB,∠BAD +∠ABC = 180º.
即得 ∠BAD = 90º.
∵ 2BD AD BC,∴ AD BD
BD BC .……………………………(1 分)
又∵ ∠CBD =∠ADB,
∴ △BCD∽△DBA.………………………………………………(1 分)
∴ ∠BDC =∠BAD = 90º.…………………………………………(1 分)
∴ ∠DBC +∠C = 90º.
∵ ∠MDB=∠ADB,∠MBD =∠ADB,
∴ ∠MBD =∠MDB.∴ BM = MD.……………………………(1 分)
又∵ ∠BDM +∠CDM =∠BDC = 90º,
∴ ∠C =∠CDM.…………………………………………………(1 分)
∴ CM = MD.∴ BM = CM.……………………………………(1 分)
(2)∵ BE⊥DM,
∴ ∠DEF =∠BDC = 90º.
∴ ∠FDE +∠DFE = 90º,∠DBF +∠DFE = 90º.
∴ ∠FDE =∠DBF.………………………………………………(1 分)
又∵ ∠FDE =∠C,
∴ ∠DBF =∠C. …………………………………………………(1 分)
于是,由 ∠FDB =∠BDC = 90º,∠DBF =∠C,
得 △FDB∽△BDC.………………………………………………(1 分)
∴ DF BD
BD CD .即 2BD DF CD.……………………………(1 分)
∵ BM = CM,∠BDC = 90º,∴ BC = 2DM.…………………(1 分)
又∵ ,
∴ 2AD DM DF DC .…………………………………………(1 分)
24.解:(1)∵ 二次函数 22 53y x b x 的图像经过点 A(5,0),
∴ 22 5 5 5 03 b . ……………………………………………(1 分)
解得 7
3b .…………………………………………………………(1 分)
∴ 二次函数的解析式是 227533y x x .………………………(1 分)
(2)当 x = 0 时,得 y = 5.∴ B(0,5).……………………………(1 分)
当 x = 3 时,得 2273 3 5 633y ,∴ C(3,6). ……(1 分)
联结 BC.
∵ 22(5 0) (0 5) 5 2AB ,
22(0 3) (5 6) 10BC ,
22(5 3) (0 6) 2 10AC ,
∴ 2 2 2AB BC AC.
∴ 90ACB .……………………………………………………(1 分)
∴ 10 1tan 22 10
BCBAC AC .……………………………………(1 分)
(3)设 D(m,n).
过点 D 作 DE⊥x 轴,垂足为点 E.则 5AE m ,DE = n.
∵ A(5,0), B(0,5), ∴ OA = OB.
又∵ 90AOB ,∴ 45BAO ,……………………………(1 分)
即得 ∠DAE +∠BAD = 45º .
又∵ ∠DAC = 45º,即 ∠BAD +∠BAC = 45º,
∴ ∠DAE =∠BAC.
又∵ ∠DEA =∠ACB = 90º,
∴ △DAE∽△BAC.…………………………………………………(1 分)
∴ 1
2
DE BC
AE AC.……………………………………………………(1 分)
∴ 1
52
n
m
.即得 1(5 )2nm.
∵ 点 D 在二次函数 227533y x x 的图像上,
∴ 22 7 15 (5 )3 3 2m m m .
解得 1
3
4m ,m2 = 5(不合题意,舍去).………………………(1 分)
∴ 1 3 23(5 )2 4 8n .
∴ 3 23( , )48D .……………………………………………………(1 分)
25.解:(1)过点 A 作 AH⊥BC,垂足为点 H,交 DE 于点 Q.
∵ ∠BAC = 90°, 32AB AC ,∴ BC = 6.…………………(1 分)
又∵ AH⊥BC,∴ 1 32BH CH BC ,Q 是△ABC 的重心.
∴ 1 13QH AH.…………………………………………………(2 分)
∵ DE // BC,PM⊥BC,AH⊥BC,
∴ PM = QH = 1.……………………………………………………(1 分)
(2)延长 FP,交 BC 于点 N.
∵ ∠BAC = 90°,AB = AC,∴ ∠B = 45°.
于是,由 FN⊥AB,得 ∠PNM = 45°.
又由 PM⊥BC,得 MN = PM = 1, 2PN .
∴ BN = BM +MN = x +1, 2 ( 1)2FB FN x .…………………(1 分)
∴ 223 2 ( 1) (5 )22AF AB FB x x ,
22( 1) 2 ( 1)22FP FN PN x x .…………………(1 分)
∵ PF⊥AB,PG⊥AC,∠BAC = 90°,∴ ∠BAC =∠PFA =∠PGA = 90°.
∴ 四边形 AFPG 是矩形.
∴ 22( 1) (5 )22y FP AF x x ,……………………………(1 分)
即 所求函数解析式为 215322y x x .…………………………(1 分)
定义域为15x.……………………………………………………(1 分)
(3)∵ 四边形 AFPG 是矩形,∴ )5(2
2 xAFPG .…………(1 分)
由 ∠FPM =∠GPM = 135°,可知,当△PMF 与△PMG 相似时,有两种
情况:∠PFM =∠PGM 或∠PFM =∠PMG.
(ⅰ)如果 ∠PFM =∠PGM,那么 PF PM
PG PM .即得 PF = PG.
∴ 22( 1) (5 )22xx .………………………………………(1 分)
解得 x = 3.即得 BM = 3.………………………………………(1 分)
(ⅱ)如果 ∠PFM =∠PMG,那么 PF PM
PM PG .即得 2PM PF PG.
∴ 22( 1) (5 ) 122xx .………………………………………(1 分)
解得 1 32x , 2 32x .
即得 32BM 或 32BM .………………………………(1 分)
∴ 当△PMF 与△PMG 相似时,BM 的长等于32 或 3 或32 .
2013 年上海市普陀区中考数学一模试卷
(测试时间:100 分钟,满分:150 分) 2013.1 月
考生注意:
1.本试卷含三个大题,共 25 题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、
本试卷上答题一律无效.
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题:(本大题共 6 题,每题 4 分,满分 24 分)
1.如果 : 2:3xy ,那么下列各式不成立的是………………………………………( ).
(A) 5
3
xy
y
; (B) 1
3
xy
y
; (C) 1
23
x
y ; (D) 13
14
x
y
.
2.某一时刻,身髙 1.6 m 的小明在阳光下的影长是 0.4 m,同一时刻同一地点测得某旗杆的影长是 5m,那
么该旗杆的高度是……………………………………………………( ).
(A)1.25m; (B)10m; (C)20 m; (D)8m.
3.如果二次函数 2y x bx c 配方后为 2( 2) 1yx- ,那么b, c 的值分别为…( ).
(A) 4 ,5; (B)4,3; (C) 4 , 3; (D)4,5.
4.如图,已知抛物线 cbxxy 2 的对称轴为 2x ,点 A, B 均在抛物线上,且 AB 与 x 轴平行,其
中点 A 的坐标为(0,3),则点 B 的坐标为……………………( ).
(A)(2,3); (B)(4,3); (C)(3,3); (D)(3,2).
5.如图所示,△ABC 的顶点是正方形网格的格点,则 sinA 的值为……………………( ).
(A) 1
2 ; (B) 5
5
; (C) 25
5
; (D) 10
10
.
6. 已知线段 a、b、c,求作第四比例线段 x,下列作图正确的是……………………( ).
O x
y
A
x = 2
B
(第 4 题) (第 5 题)
a
x
b c
a
c
b x
x
c
b a
x
c
a
c
x b
(A) (B) (C) (D)
二、填空题:(本大题共 12 题,每题 4 分,满分 48 分)
7.如果在比例尺为 1︰1 000 000 的地图上,A、B 两地的图上距离是 1.6 厘米,那么 A、B 两地的实际距离
是 千米.
8.把长度为 4cm 的线段进行黄金分割,则较长线段的长是__________cm.
9.如果两个相似三角形的对应角平分线比是 1︰4,那么它们的周长比是 .
10.如果抛物线 21) 2 1y m x mx ( 的图像开口向下,那么 m 的取值范围是__________.
11.将二次函数 22yx 的图像向右平移 1 个单位,再向下平移 2 个单位,所得图像的解析式
为 ________________.
12.二次函数 2y ax bx c 中,函数 y 与自变量 x 的部分对应值如下表,则 m 的值为__________ .
2 1 0 1 2 3 4
7 2 2 m 2
13.在 Rt△ABC 中,∠C=90°, B ,AB=2,那么 BC= _____________.(结果用 的锐角三角比表示)
14.如图,点 D、E、F 分别是△ABC 三边的中点,那么与 DF 相等的向量是__________ .
15.如图,点 G 是△ABC 的重心,AG⊥GC,AC=4,那么 BG 的长为 ___________.
16.如图,△ABC 中,∠C=90°,BC=6cm,cot
2
3A ,那么△ABC 的面积是____________ cm2.
17.如图,某公园入口处原有三级台阶,每级台阶高为 18cm,深为 30cm,为方便残疾人士,拟将台阶改为
斜坡,设台阶的起点为 A,斜坡的起始点为 C,现设计斜坡 BC 的坡度 1:5i ,那么 AC 的长度是 cm.
18. 如图,在△ABC 中,∠C=90°,将△ABC 沿直线 MN 翻折后,顶点 C 恰好落在 AB 边上的点 D 处,已
知 MN∥AB,MC=6,NC= 23,那么四边形 MABN 的面积是______________.
(第 14 题) (第 15 题) (第 16 题)
(
(第 17 题) (第 18 题)
三、解答题:(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
计算:
2 cot 30cos30 (sin 60 )
2 cos45
.
20.(本题满分 10 分)
如图,已知两个不平行的向量 a 、b .
先化简,再求作: 13( 3 ) ( )22a b a b .
(不要求写作法,但要指出所作图中表示结论的向量)
21.(本题满分 10 分)
已知:在直角梯形 ABCD 中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接 BD,AE⊥BD,垂足为点 E.
(1)求证:△ABE∽△DBC;
(2)求线段 AE 的长.
b
a
(第 20 题图)
(
(第 21 题)
(
(第 22 题)
22.(本题满分 10 分)
21.3 , 0
63.5
9 2 9 sin21.3 , tan 21.3 ,sin 63.5 , tan 63.5 2)25 5 10
AC
BC
C
一艘轮船自西向东航行,在 处测得东偏北 方向有一座小岛 继续向东航行8
海里到达 处,测得小岛 此时在轮船的东偏北 方向上。之后,轮船继续向东航
行多少海里,距离小岛 最近?
(参考数据:
C
A B
23.(本题满分 12 分,其中第(1)小题 3 分,第(2)小题 4 分, 第(3)小题 5 分)
如图,点 E 是矩形 ABCD 的边 BC 上一点,EF⊥AE,
EF 分别交 AC、CD 于点 M、F,BG⊥AC,垂足为点 G,
BG 交 AE 于点 H.
(1)求证:△ABE∽△ECF;
(2)找出与△ABH 相似的三角形,并证明;
(3)若 E 是 BC 中点,BC=2AB,AB=2,求 EM 的长.
(第 23 题)
24.(本题满分 12 分,其中第(1)小题 2 分,第(2)小题 5 分,第(3)小题 5 分)
如图,点 A 在 x 轴上,OA=4,将线段 OA 绕
点 O 顺时针旋转 120°至 OB 的位置.
(1)求点 B 的坐标;
(2)求经过点 A、O、B 的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点 P,
使得以点 P、O、B 为顶点的三角形是等腰三角形?
若存在,求点 P 的坐标;若不存在,说明理由.
25.(本题满分 14 分,其中第(1)小题 3 分,第(2)小题 5 分,第(3)小题 6 分)
将△ABC 绕点 A 按逆时针方向旋转 θ 度,并使各边长变为原来的 n 倍,得△AB′C′,即如图①,我们
将这种变换记为[θ,n].
(1)如图①,对△ABC 作变换[60°, 3 ]得△AB′C′,那么 AB C
ABC
S
S
= ;
直线 BC 与直线 B′C′所夹的锐角为 度.
(2)如图②,△ABC 中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',
使点 B、C、C′在同一直线上,且四边形 ABB'C'为矩形,求 θ 和 n 的值.
(3)如图③,△ABC 中,AB=AC,∠BAC=36°,BC=l,对△ABC 作变换[θ,n]得△AB′C′,使点 B、C、B′
在同一直线上,且四边形 ABB'C'为平行四边形,求 θ 和 n 的值.
(
(第 24 题)
2013 年上海市普陀区中考数学一模试卷
参考答案及评分说明
一、选择题(本大题共 6 题,每题 4 分,满分 24 分)
1.(D); 2. (C); 3.(A); 4.(B); 5.(B); 6.(D).
二、填空题(本大题共 12 题,每题 4 分,满分 48 分)
7.16; 8.( 2 5 2 ); 9.1︰4; 10. 1m ; 11. 22( 1) 2yx ;
12. 1 ; 13. 2cos ; 14. EA 和 CE ; 15.4; 16.12; 17.210 ; 18.18 3 .
三、解答题:(本大题共 7 题,满分 78 分)
19.解:原式 23 3 3()22 22 2
……………………………………………………(4 分)
33 324 ………………………………………………………………(4 分)
53
8 . …………………………………………………… ……………(2 分)
20. 解: 13( 3 ) ( )22a b a b
13322a b a b ………………………………………………………(1 分)
2ab …………………………………………………………………(4 分)
画图正确 4 分(方法不限),结论 1 分.
21.(1)证明:∵AB=AD=25,∴∠1 =∠2.……………… (1 分)
∵AD∥BC,∴∠1=∠3.……………………(1 分)
∴∠2=∠3. …………………………………(1 分)
∵AE⊥BD,
∴∠AEB=∠C=90°. ………………………(1 分)
∴△ABE∽△DBC. ………………………(1 分)
(2)解:∵AB=AD,又 AE⊥BD,∴BE=DE.
1
2 3
∴BD=2BE.…………………………………………………………………(1 分)
由△ABE∽△DBC,得 AB BE
BD BC . ……………………………………(1 分)
∵AB=AD=25,BC=32,∴ 25
2 32
BE
BE .
∴BE=20. ………………………………………………………………(2 分)
∴ 22AE AB BE 2225 20 (25 20) (25 20)
=15. ……………………………………………………………………(1 分)
22.解:过点 C 作 CD⊥AE,垂足为点 D,
此时轮船离小岛最近,BD 即为所求.………(1 分)
由题意可知:
∠A=21.3°,AB=80 海里,∠CBE=63.5°.…(1 分)
在 Rt△ACD 中,tan∠A= CD
AD 2
5
,……………………………………………(1 分)
2(80 )5CD BD;………………………………………………………(1 分)
同理: 2CD BD ;………………………………………………………………(2 分)
∴ 22 (80 )5BD BD,…………………………………………………………(2 分)
解得: 20BD .…………………………………………………………(1 分)
C 答:轮船继续向东航行20海里,距离小岛 最近. ……………………………………(1 分)
23.
(1)证明:∵四边形 ABCD 是矩形,
∴∠ABE=∠ECF=90°.………………(1 分)
∵AE⊥EF,∴∠1+∠2=90°.
又∵∠1+∠3=90°,
∴∠3=∠2, …………………………(1 分)
∴△ABE∽△ECF. …………………(1 分)
(2)答:△ABH∽△ECM.………………………(1 分)
证明:∵BG⊥AC,∠ABE=90°,
∴∠4+∠BAG=∠5+∠BAG= 90°.
∴∠4=∠5.………………………………………………………………………(1 分)
由(1)知,∠3=∠2,…………………………………………………………(1 分)
∴△ABH∽△ECM.………………………………………………………………(1 分)
(3)解:过点 M 作 MR⊥BC,垂足为 R.…………………………………………………(1 分)
∵AB=BE=EC=2,
∴AB∶BC=MR∶RC=1∶2,…………………………………………………… (1 分)
∠1=45°,CR=2MR,
1 2
3
4
5
C
A B D E
∴∠2=45°,………………………………………………………………………(1 分)
∴ER=MR, ………………………………………………………………………(1 分)
∴MR= 2
3
,∴ 2 2 2233EM .……………………………………………(1 分)
24. 解:
(1)如图,过点 B 作 BC⊥ x 轴,垂足为的点 C.
……………………………………………(1 分)
∵∠AOB=120°,∴∠BOC=60°.又∵OA=OB=4,
∴ =2OC , =2 3BC .
∴点 B 的坐标为(﹣2,﹣ 23).…………………………………………………(2 分)
(2)∵抛物线过原点 O 和点 A、B,
∴可设抛物线的解析式为 2 ( 0)y ax bx a ,……………………………………(1 分)
将 A(4,0), B(﹣2,﹣ 23)代入,得
16 4 0,
4 2 2 3.
ab
ab
……………………………………………………………………(2 分)
解得
3 ,6
23.3
a
b
∴此抛物线的解析式为 3 2 3
63yx .………………………………………………(2 分)
(3)存在.……………………………………………………………………………………(1 分)
解:如图,抛物线的对称轴是 =2,直线 =2 与 轴的交点为 D,
设点 P 的坐标为(2,y).
①若 OB=OP,则 22+|y|2=42,解得 y=±23,
当 y= 时,在 Rt△POD 中,∠PDO=90°,
sin∠POD= PD
OP
3
2 ,∴∠POD=60°.
∴∠POB=∠POD+∠AOB=60°+120°=180°,
即 P、O、B 三点在同一直线上.∴y= 23不符合题意,舍去.
∴点 P 的坐标为(2,﹣ ).………………………………………………………(1 分)
②若 BO=BP,则 42+|y+ |2=42,解得 y=﹣ .
∴点 P 的坐标为(2,﹣ ).……………………………………………………………(1 分)
③若 PO=PB,则 22+|y|2=42+|y+ |2,解得 y=﹣ .
∴点 P 的坐标为(2,﹣ ).……………………………………………………………(1 分)
综上所述,符合条件的点 P 只有一个,其坐标为(2,﹣ ).…………………(1 分)
25.
解:(1) 3;60. …………………………………………………………………………(2 分)
(2)∵四边形 ABB′C′是矩形,∴∠BAC′=90°.………………………………………(1 分)
∴θ=∠CAC′=∠BAC′﹣∠BAC=90°﹣30°=60°.……………………………………(1 分)
在 Rt△AB B' 中,∠ABB'=90°,∠BAB′=60°,∴∠AB′B=30°.…………………(1 分)
∴AB′=2 AB,即 2ABn AB
.……………………………………………………(1 分)
(3)∵四边形 ABB′C′是平行四边形,∴AC′∥BB′.
又∵∠BAC=36°,∴θ=∠CAC′=∠ACB=72°. …………………………………(1 分)
∴∠C′AB′=∠BAC=36°. …………………………………………………………(1 分)
而∠B=∠B,∴△ABC∽△B′BA. ………………………………………………(1 分)
∴AB∶BB′=CB∶AB. ……………………………………………………………(1 分)
∴AB2=CB•BB′=CB(BC+CB′). …………………………………………………(1 分)
而 CB′=AC=AB=B′C′,BC=1,∴AB2=1(1+AB), ………………………………(1 分)
解得,AB
15
2
.…………………………………………………………………(1 分)
∵AB>0,∴
51
2
BCn BC
.…………………………………………………(1 分)
(以上各题,若有其他解法,请参照评分标准酌情给分)
2012 学年第一学期徐汇区初三年级数学学科
期终学习能力诊断卷 2013、1
(时间 100 分钟 满分 150 分)
考生注意∶
1.本试卷含三个大题,共 25 题;答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、
本试卷上答题一律无效;
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一.选择题(本大题共 6 题,每题 4 分,满分 24 分)
【下列各题的四个选项中,有且只有一个选项是正确的】
1.在 ABCRt 中, 90C , 5AC , 13AB ,那么 Atan 等于…………( )
A.
13
5 ; B.
12
5 .; C.
5
12 ; D.
5
13 .
2.将抛物线 2xy 沿 y 轴向上平移 1 个单位后所得抛物线的解析式是 …………( )
A. 12 xy ; B. 12 xy ; C. 2)1( xy ; D. 2)1( xy .
3.坡比等于 1∶ 3 的斜坡的坡角等于 ………………………………………………( )
A. 30 ; B. 45 ; C. 50 ; D. 60 .
4.关于二次函数 2)2( xy 的图像,下列说法正确的是…………………………( ).
A.开口向下; B.最低点是 )0,2( ;
C.对称轴是直线 2x ; D.对称轴的右侧部分是上升的.
5.如图 1, BDAC、 相交于点O ,下列条件中能判定CD ∥ AB 的是 …………( )
A.
CO
BO
DO
AO ; B.
CD
AB
CO
AO ;
C.
AO
CO
DO
BO ; D.
BD
BO
AC
AO .
6.如图 2,在 中, 90ACB , ABCD 垂足为 D ,那么下列结论中错误的
是………………………………………………………………………………………( )
A. ADBCBDAC 22 ; B. ABCDBDBC 22 ;
C. CDACBCAD ; D. BDACBCCD .
二.填空题(本大题共 12 题,每题 4 分,满分 48 分)
7.计算: 45tan60sin2 .
8.计算: )2(2
1 baba
.
9.抛物线 342 2 xxy 与 y 轴的交点坐标是 .
A
C
D
B
(图 2)
A B
C D
E F
(图 3)
B
C D
A
O
(图 1)
10.如果两个相似三角形对应角平分线的比是 3:2 ,那么它们对应高的比是 .
11.如图 3,已知 AB ∥CD ∥ EF , 3:2: CEAC , 15BF ,那么 BD .
12.点C 是线段 AB 上一点, ACBC 2 ,点 NM、 分别是线段 BCAC、 的中点,那么
BCMN : 等于 .
13.抛物线 cbxaxy 2 过 )0,1( 和 )0,5( 两点 ,那么该抛物线的对称轴是 .
14.在以 O 为坐标原点的直角坐标平面内有一点 A(2,4), 如果 AO 与 x 轴正半轴的夹角
为 ,那么 αcos = .
15.小明同学身高 1.5 米,经太阳光照射,在地面的影长为 2 米,他此时测得旗杆在同一地
面的影长为 12 米,那么旗杆高为 __ 米.
16.抛物 线 32 bxaxy 与 x 轴交于 点 BA、 (点 A 在点 B 的 左侧 ),与 y 轴交 于点 C ,且
3:1: OBOA , OCOB ,那么 a 的值是 .
17.两个等腰直角三角形 ACB 和 DCE 的位置如图 4 所示,
点 ECA 、、 和点 DCB 、、 分别在一直线上, 90ACB ,
24AE , DEAB 3 ,点 HG、 分别是 ACB 、
DCE 的重心,联结GH ,那么 GH .
18.在 ABCRt 中, 90C , 5AB , 4AC ,点 D 是斜边 AB 的中点,把 ABC 绕点C 旋转,
使得点 B 落在射线CD 上,点 A 落在点 A .那么 AA 的长是_____________.
三.(本大题共 7 题,第 19—22 题每题 10 分;第 23、24 题每题 12 分;第 25 题 14 分;
满分 78 分)
19.(本题满分 10 分)
抛物线 cxaxy 22 经过点 )0,3(B 、 )3,0(C 两点.
(1)求抛物线顶点 D 的坐标; (5 分)
(2)抛物线与 x 轴的另一交点为 A ,求 ABC 的面积. (5 分)
20.(本题满分 10 分)
如图 5,在 ABC 中,点 D 是边 AB 的中点, ACAB 2 , 4BC .
(1)求CD 的长; (5 分)
(2)设 AB a , AC =b
,求向量CD (用向量 a 、 b 表示). (5 分)
G
C
A B
D E
H
(图 4)
A
B C
D
(图 5)
21.(本题满分 10 分)
如图 6,在 ABC 中, BE 平分 ABC 交 AC 于点 E ,过点 E 作 ED ∥ BC 交 AB 于
点 D .
(1)求证: ACBDBCAE ; (5 分)
(2)如果 3ADES , 2BDES , 6DE ,求 BC 的长. (5 分)
22.(本题满分 10 分)
如图 7,小岛 B 正好在深水港口 A 的东南方向,一艘集装箱货船从港口 出发,沿正东方向以每小时
30 千米的速度行驶,40 分钟后在C 处测得小岛 在它的南偏东 15 方向,求小岛 离开深水港口 的
距离.(精确到 1.0 千米)
参考数据: 41.12 , 45.26 , 26.015sin , 97.015cos , 27.015tan .
A
B C
D E
(图 6)
A
B
C
北
北
(图 7)
23.(本题满分 12 分)
“数学迷”小楠通过从“特殊到一般”的过程,对倍角三角形(一个内角是另一个内角的 2 倍的三角形)
进行研究.得出结论:如图 8,在 ABC 中, CBA 、、 的对边分别是 cba 、、 ,如果 BA 2 ,
那么 bcba 22 .
下面给出小楠对其中一种特殊情形的一种证明方法.
已知:如图 9,在 中, 90A , 45B .
求证: .
证明:如图 9,延长CA 到 D ,使得 ABAD .
∴ ABDD ,
∵ DABDDCAB 2 , 90CAB
∴ 45D ,∵ 45ABC ,
∴ ABCD ,又 CC
∴ ABC ∽ BCD
∴
BC
AC
CD
BC ,即
a
b
cb
a
∴ bcba 22
根据上述材料提供的信息,请你完成下列情形的证明(用不同于材料中的方法也可以):
已知:如图 8,在 中, .
求证: .
b
C
A
B a
c
(图 8)
A
C
B
a b
c
(图 9)
D
24.(本题满分 12 分)
抛物线 nmxmxy 52 与 y 轴正半轴交于点C ,与 x 轴分别交于点 A 和点 )0,1(B ,
且 OBOAOC 2 .
(1)求抛物线的解析式; (6 分)
(2)点 P 是 轴上一点,当 PBC 和 ABC 相似时,求点 的坐标. (6 分)
25.(本题满分 14 分)
梯形 ABCD 中, AB ∥CD , 10CD , 50AB ,
5
4cos A , 90BA ,
点 M 是边 的中点,点 N 是边 AD 上的动点.
(1)如图 10,求梯形 的周长; (4 分)
(2)如图 11,联结 MN ,设 xAN , yNMAMN cos ( 0 < NMA < 90 ),求 关于 的关系
式及定义域; (4 分)
(3)如果直线 与直线 BC 交于点 P ,当 AP 时,求 AN 的长. (6 分)
B
C D
A
(图 10)
N
M B
C D
A
(图 11)
B
C D
A
(备用图)
M
2012 学年第一学期徐汇区初三年级数学学科
期终学习能力诊断卷参考答案和评分标准
一、选择题:(本大题共 6 题,每题 4 分,满分 24 分)
1.C; 2.B; 3.A; 4.D; 5.D; 6.B.
二.填空题:(本大题共 12 题,满分 48 分)
7. 3 ; 8. b
2
3 ; 9. )3,0( ; 10. 3:2 ; 11.6 ; 12. 4:3 (或
4
3 );
13.直线 2x ; 14.
5
5 ; 15.9 ; 16.1或 1 ; 17.
3
22 (或
3
8 ); 18.
5
58 .
三、(本大题共 7 题,第 19、20、21、22 题每题 10 分,第 23、24 题每题 12 分,第 25 题 14 分,满分 78
分)
19. 解:(1)由题意,得
;3
,069
c
ca ………………………………………(1 分)
解得
;3
,1
c
a ………………………………………………………(1 分)
∴ 322 xxy ………………………………………………(1 分)
∴ )4,1(D ……………………………………………………………(2 分)
(2)由题意,得 0322 xx ,解得 3,1 21 xx ;
∴ )0,1(A …………………………………………………………(2 分)
又 )0,3(B 、 )3,0(C
∴ 6342
1 ABCS …………………………………………(3 分)
20.解:(1)∵点 D 是边 AB 的中点, ACAB 2 ,∴ ACABAD 2
2
2
1 (1 分)
∴
2
2AC
AD ,
2
2
2
1 AB
AC ………………………………(1 分)
∴
AB
AC
AC
AD ,又 AA .∴ ADC ∽ ACB ……………(1 分)
∴
AB
AC
BC
CD ,即
2
2
4 CD ,∴ 22CD …………………(2 分)
(2)∵点 D 是边 AB 的中点,∴ AD aAB
2
1
2
1 …………………(2 分)
∴ CD AD baAC
2
1 .…………………………………(3 分)
21.(1)证明:∵ BE 平分 ABC ,∴ CBEABE .……………………(1 分)
∵DE∥BC ,∴ CBEDEB ……………………………(1 分)
∴ DEBABE .∴ DEBD ……………………………(1 分)
∵DE∥BC ,∴
BC
DE
AC
AE ……………………………………(1 分)
∴
BC
BD
AC
AE ,∴ ACBDBCAE ………………………(1 分)
(2)解:设 ABE 中边 AB 上的高为 h .
∴
2
3
2
1
2
1
BD
AD
hBD
hAD
S
S
BDE
ADE ,…………………………………(2 分)
∵DE∥BC,∴
AB
AD
BC
DE . ………………………………………(1 分)
∴
5
36 BC
,∴ 10BC . …………………………………………(2 分)
22.解: 由题意,得 203
230 AC . ……………………………………(2 分)
【方法一】过点C 作 ABCD ,垂足为 D .……………………………………(1 分)
在 ADCRt 中, 90ADC , 45CAD
∴ 21045cos ACAD , 21045sin ACCD ……(2 分)
在 BDCRt 中, 90BDC , 30154590B …(1 分)
∴ 61030cot CDBD …………………………………………(2 分)
∴ )62(10 BDADAB ≈ 6.38)45.241.1(10 .…(2 分)
【方法二】过点 B 作 ACBD ,交 AC 延长线于 . ………………………(1 分)
在 BDCRt 中, 90BDC , 15CBD
设 xBD ,∴ xBDCD 27.015tan . ………………………(2 分)
∵ DABDABABD 45459090 ……………(1 分)
∴ BDAD ,∴ xx 27.020 ,得
73.0
20x ……………………(2 分)
∴ 6.3873.0
2041.173.0
2022 BDAB …………………(2 分)
答:小岛 B 离开深水港口 A 的距离是 6.38 千米.
23.证明: 延长CA 到 D ,使得 ABAD .……………………………………(2 分)
∴ ABDD ,……………………………………………………(2 分)
∵ DABDDCAB 2 ,………………………………(2 分)
∵ ABCCAB 2 ,∴ ABCD ,又 CC
∴ ABC ∽ BCD …………………………………………………(2 分)
∴
BC
AC
CD
BC ,即
a
b
cb
a
………………………………………(2 分)
∴ bcba 22 ………………………………………………………(2 分)
24.解:(1)由题意,得抛物线对称轴是直线
2
5x ,……………………………(1 分)
∵点 A 和点 B 关于直线 对称,点 )0,1(B ,∴ )0,4(A ………(1 分)
∵ 4142 OBOAOC ,∴ 2OC …………………………(1 分)
∵点C 在 y 轴正半轴上,∴ )2,0(C ………………………………(1 分)
∴ 22
5
2
1 2 xxy ………………………………………………(2 分)
(2)由题意,可得 3AB , 5BC , 52AC …………………(1 分)
∵ OBOAOC 2 ,∴
OA
OC
OC
OB ,又 COABOC
∴ BOC ∽ COA ,∴ OACOCB ………………………(1 分)
∴ PBC 和 ABC 相似时,分下列两种情况:
1 当
AC
AB
BC
CP 时,得
52
3
5
CP ,∴
2
3CP ,
∴
2
1
2
32 CPOCOP ,∴ )2
1,0(P .………………………(2 分)
2 当
AB
AC
BC
CP 时,得
3
52
5
CP ,∴
3
10CP ,
∴
3
423
10 OCCPOP ,∴ )3
4,0( P .………………(2 分)
综合 21 、 ,当 和 相似时 或 .
25.解:(1)过点C 作CF ∥ AD ,交 AB 于点 F .………………………………(1 分)
∴ ACFB ,∵ 90BA ,
∴ 90BCFB ,∴ 90FCB
∵ AB ∥CD ,∴四边形CDAF 是平行四边形;
∴ ADCF , 10 CDAF ,∴ 40 AFABBF
在 BCFRt 中, 90FCB ,∴
BF
CFCFB cos ,
∴ ADCFBBFCF 325
440cos ………………………(1 分)
∴ 243240 2222 CFBFBC …………………………(1 分)
∴ 11624503210 ABCDC .…………………………………(1 分)
(2)过点 N 作 ABNQ ,垂足为Q .∴ 90NQMNQA ,…(1 分)
∴
AN
AQA cos ,∴ xAANAQ 5
4cos ,
∴
MN
MQNMA cos ,∴ yNMAMNMQ cos ,
∵点 M 是边 AB 的中点,∴ 252
1 ABAM ,
∴ xy 5
425 ;…………………………………………………………(2 分)
定义域是0 < x <
4
125 .…………………………………………………(1 分)
(3)分别延长 BCAD、 交于点 E ,联结 EM .
∵ 90BA ,∴ 90AEB , 25 BMEMAM ;
∴ 405
450cos AABAE .
直线 MN 与直线 BC 交于点 P ,当 AP 时,分两种情况:
1 当点 P 在CB 的延长线上时,
∵ EMBM ,∴ EBMBEM ;∵ 90ABEA ,
∴ 90MEBP ,∴ 90EMNEMP ;
∵ EMAM ,∴ AAEM ;∴
EN
EMAEM cos ,
∴
4
125
5
4
25
cos A
EMEN ;∴
4
35
4
12540 ENAEAN .…(3 分)
2 当点 在 BC 的延长线上时,
∵ 90PNEP , PNEANM ,∴ 90ANMA ,
∴ 90AMN ,∴
AN
AMA cos ,∴
4
125
5
4
25
cos A
AMAN .…(3 分)
综合 、 2 ,当 时,
4
35AN 或
4
125 .
2013 年上海市闸北区中考数学一模试卷
(2013 年 1 月)
(考试时间:100 分钟,满分:150 分)
考生注意:
1、本试卷含三个大题,共 25 题;
2、答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3、除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要
步骤.
一、 选择题(本大题共 6 题,每题 4 分,满分 24 分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位
置上.】
1.抛物线 y=-x2 向左平移 2 个单位后所得的抛物线解析式是………………( )
(A)y=-x2-2; (B)y=-(x-2)2;
(C)y=-(x+2)2; (D)y=-x2+2.
2.已知 D、E 分别在△ ABC 的 BA、CA 的延长线上,下列给出的条件中能判定 ED∥BC 的
是………………………………………………………………………………………( )
(A)
AD
AE =
AC
AB ; (B)
BD
AB =
CE
AC ;
(C)
BC
DE =
AB
AD ; (D)
BC
DE =
CE
BD .
3.在 Rt△ABC 中,∠C=90°,∠B=α,AC=b,那么 AB 等于……………( )
(A)
cos
b
; (B)
sin
b
; (C)
tan
b
; (D)
cot
b
.
4.如果四条线段 a、b、c、d 构成
b
a =
d
c ,m>0,则下列式子中,成立的是……( )
(A)
a
b =
d
c ; (B)
b
a =
md
mc
;
(C)
b
ba =
d
cd ; (D)
db
ca
= .
5.在△ABC 中,中线 AD、BE 相交于点 O,且 S△ BOD=5,则△ ABC 的面积是( )
(A)30; (B)20; (C)15; (D)5.
6.根据二次函数 y=-x2+2x+3 的图像,判断下列说法中,错误..的是………( )
(A)二次函数图像的对称轴是直线 x=1;
(B)当 x>0 时,y<4;
(C)当 x≤1 时,函数值 y 是随着 x 的增大而增大;
(D)当 y≥0 时,x 的取值范围是-1≤x≤3 时.
二、填空题(本大题共 12 题,每题 4 分,满分 48 分)
7.钓鱼岛列岛是我国最早发现、命名,并行使主权的.在一幅比例尺是 1︰100000 的地图上,测得钓
鱼岛的东西走向长为 3.5 厘米,那么它的东西走向实际长大约为 ▲ 米.
8.已知点 D 是线段 AB 的黄金分割点,且线段 AD 的长为 2 厘米,则最短线段 BD 的长是 ▲ 厘
米.
9.如果 a +b =2( -3 ),那么用 表示 ,得 = ▲ .
10.抛物线 y= 4x2+2x-1 有最 ▲ 点(填“高”、“低”).
11.某印刷厂一月份印书 50 万册,如果从二月份起,每月印书量的增长率都为 x,那么三月份的印书
量 y(万册)与 x 的函数解析式是 ▲ .
12.在坡度为 i=1︰2.4 的斜坡上每走 26 米就上升了 ▲ 米.
13.如图一,已知点 D、E 分别在△ ABC 的边 AB
和 AC 上,且 DE∥BC,S△AED︰S 梯形 EDBC=1︰2,则
AE︰AC 的比值是 ▲ .
14.若二次函数 y=mx2-(2m-1)x+m 的图像
顶点在 y 轴上,则 m= ▲ .
15.如图二,在 Rt△ ABC 中,∠C=90°,点 D
在边 BC 上,且∠ADC+∠B=90°,DC=3,BD=6,
则 cosB= ▲ .
16.如图三,在边长相同的小正方形组成的网格
中,点 A、B、C 都在这些小正方形的顶点上,则
∠ABC 的正切值是 ▲ .
17.如图四,在△ABC 中,AB=AC,∠A=36°,
BD 平分∠ABC 交 AC 于点 D,DE 平分∠BDC 交 BC
于点 E,则
AD
EC = ▲ .
18.如图五,在 Rt△ ABC 中,AB=6cm,BC=
4cm,点 D 是斜边 AB 上的中点,把△ ADC 沿着 AB
方向平移 1cm 得△ EFP,EP 与 FP 分别交边 BC 于
点 H 和点 G,则 GH= ▲ .
三、解答题(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
计算:
145sin2
1
-2 2)30cot1( +sin260°+cos260°.
(
图
一
)
D
A
B C
E
(
图
三
)
A
B
C
(
图
二
)
D
A B
C
(
图
四
)
E
D
A
B C
(
图
五
)
H
F
G
E D A B
C P
(
图
六
)
H F E
D A B
C
(
图
七
)
N
O
M
D A
B C
20.(本题满分 10 分 第(1)小题 4 分,第(2)小题 6 分)
已知:二次函数 2 (y ax bx c a ≠0) 的图像经过点(3,5)、(2,8)、(0,8).
(1)求这个二次函数的解析式;
( 2 ) 已 知 抛 物 线 2
1 1 1 1 1(y a x b x c a ≠ 0 , 2
2 2 2 2 2(y a x b x c a ≠ 0 , 且 满 足
111
222
(a b c kka b c ≠0,1 ,则我们称抛物线 12yy与 互为“友好抛物线”,请写出当 1
2k 时第(1)小
题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
21.(本题满分 10 分)
已知:如图六,九年级某班同学要测量校园内旗杆
CH 的高度,在地面的点 E 处用测角器测得旗杆顶点 C
的仰角∠CAD=45°,再沿直线 EF 向着旗杆方向行走
10 米到点 F 处,在点 F 又用测角器测得旗杆顶点 C 的
仰角∠CBA=60°;已知测角器的高度为 1.6 米,求旗
杆 CH 的高度(结果保留根号).
22.(本题满分 10 分)
已知:如图七,在平行四边形 ABCD 中,对角线
AC、BD 相交于点 O,点 M、N 分别在边 AO 和边 OD
上,且 AM=
3
2 AO,ON=
3
1 OD,设 AB = a , BC
=b ,试用 、 的线性组合表示向量OM 和向量 MN .
23.(本题满分 12 分 第(1)小题 6 分,第(2)小题 6 分)
已知:如图八,在△ ABC 中,BD⊥AC 于点 D,
CE⊥AB 于点 E,EC 和 BD 相交于点 O,联接 DE.
(1)求证:△ EOD∽△BOC;
(2)若 S△ EOD=16,S△ BOC=36,求 AE
AC
的值.
24.(本题满分 12 分 第(1)小题 6 分,第(2)小题 6 分)
已知:如图九,二次函数 2
3y x2 4
3 x 16
3 的图
像与 x 轴交于点 A、B(点 A 在点 B 的左侧),抛物线的
顶点为 Q,直线 QB 与 y 轴交于点 E.
(1)求点 E 的坐标;
(2)在 x 轴上方找一点 C,使以点 C、O、B 为顶点
的三角形与△ BOE 相似,请直接写出点 C 的坐标.
(
图
八
)
E
O
D
A
B C
(
图
九
)
E
O
Q
x
B A
y
25.(本题满分 14 分 第(1)小题 4 分,第(2)小题 4 分,第(3)小题 6 分)
已知:如图十,在△ ABC 中,AB=AC=15,
cos∠A=
5
4 .点 M 在 AB 边上,AM=2MB,点 P 是
边 AC 上的一个动点,设 PA=x.
(1)求底边 BC 的长;
(2)若点 O 是 BC 的中点,联接 MP、MO、OP,
设四边形 AMOP 的面积是 y,求 y 关于 x 的函数关系
式,并出写出 x 的取值范围;
(3)把△ MPA 沿着直线 MP 翻折后得到△ MPN,
是否可能使△ MPN 的一条边(折痕边 PM 除外)与 AC
垂直?若存在,请求出 x 的值;若不存在,请说明
理由.
(
图
十
)
C O
P
B
A
M
(
备
用
图
)
·
C B
A
M
(
备
用
图
)
·
C B
A
M
2013 年上海市闸北区中考数学一模试卷
答案及评分参考
(考试时间:100 分钟,满分:150 分)
一、选择题(本大题共 6 题,每题 4 分,满分 24 分)
题号 1 2 3 4 5 6
答案 C B B D A B
二、填空题(本大题共 12 题,每题 4 分,满分 48 分)
7、3500. 8、 5 -1. 9、 1
7 a .
10、低. 11、 250( 1)yx或 250 100 50y x x 12、10.
13、 3
3
. 14、 1
2
. 15、 3
2
.
16、2. 17、 35
2
. 18、 2
3
.
三、解答题(本大题共 12 题,满分 78 分)
19、(本题满分 10 分)
解: 2 2 21 2 (1 cot 30 ) sin 60 cos 602sin 45 1
=
2
221 3 12 (1 3) ( )222212
……………………………………(4 分)
= 1 3 12( 3 1) 4421
………………………………………………………(4 分)
= 2 1 2 3 2 1 ………………………………………………………………(1 分)
= 2 2 3 4………………………………………………………………………(1 分)
20、(本题满分 10 分第(1)小题 4 分,第(2)小题 6 分)
(1)根据题意,得
8
4 2 8
9 3 5
c
a b c
a b c
可以解得
1
2
8
a
b
c
…………………………(3 分)
∴这个抛物线的解析式是 2 28y x x .……………………………………(1 分)
(2)根据题意,得
2 2 2
1 2 8 1
2a b c
或 1 1 1 1
1 2 8 2
a b c
解得 2 2 22, 4, 16a b c 或 1 1 1
1 , 1, 42a b c ……………………(2 分)
友好抛物线的解析式是: 22 4 16y x x 或 21 42y x x ……………(2 分)
∴它的顶点坐标是(1, 18 )或( 91, 2 )……………………………………(2 分)
(
图
六
)
H F E
D A B
C
(
图
七
)
N
O
M
D A
B C
21、(本题满分 10 分)
根据题意,设 DB= x 米在 Rt△CBD 中,∠CBD=60°
∴CD=DB·tan60°= 3x 米……………(2 分)
在 Rt△ACD 中,∠CAD=45°
∴CD=AD= 米………………………(2 分)
∴ + =10…………………………………………………………………………(2 分)
解得 (5 3 5)x 米…………………………………………………………………(1 分)
CD= 3 (5 3 5) (15 5 3) 米…………………………………………………(1 分)
∴CH=15 5 3 1.6 (16.6 5 3) 米……………………………………………(1 分)
答:旗杆 CH 的高度是(16.6 5 3) 米.……………………………………………(1 分)
22、(本题满分 10 分)
∵ AC AB BC= ab ……………………………(1 分)
∵平行四边形 ABCD
∴ 1
2AO AC …………………………………………(1 分)
∴ 11()22AO AC a b ……………………………(1 分)
∵ 2
3AM OA 即 1
3OM AO
∴ 1
3OM AO ………………………………………………………………………(1 分)
∴ 1 1 1()6 6 6OM a b a b …………………………………………………(1 分)
∵AM= 2
3 AO,ON= 1
3 OD
∴ 1
3
OM ON
OA OD……………………………………………………………………(1 分)
∴MN∥AD ………………………………………………………………………(1 分)
∴ 1
3
MN OM
AD AO……………………………………………………………………(1 分)
∴ 1
3MN AD ………………………………………………………………………(1 分)
又∵平行四边形 ABCD
∴ AD BC b
∴ 1
3MN b …………………………………………………………………………(1 分)
23.(本题满分 12 分 第(1)小题 6 分,第(2)小题 6 分)
(1)证明:在△BOE 与△DOC 中
∵∠BEO=∠CDO,∠BOE=∠COD
∴△BOE∽△COD………………………………………(2 分)
∴ OE OB
OD OC ……………………………………………(1 分)
即 OE OD
OB OC ……………………………………………(1 分)
又∵∠EOD=∠BOC……………………………………(1 分)
∴△EOD∽△BOC………………………………………(1 分)
(2) ∵△EOD∽△BOC
∴ 2()EOD
BOC
S OD
S OC
………………………………………………………………(1 分)
∵S△EOD=16,S△BOC=36
∴ 2
3
OD
OC ………………………………………………………………………(1 分)
在△ODC 与△EAC 中
∵∠AEC=∠ODC,∠OCD=∠ACE
∴△ODC∽△AEC………………………………………………………………(1 分)
∴ OD OC
AE AC ……………………………………………………………………(1 分)
即 OD AE
OC AC ……………………………………………………………………(1 分)
∴ 2
3
AE
AC ………………………………………………………………………(1 分)
24.(本题满分 12 分第(1)小题 6 分,第(2)小题 6 分)
(1)令 y=0,得 22 4 16 03 3 3xx …………………(1 分)
解方程得 122, 4xx
(4,0)B …………………(1 分)
又 22 ( 1) 63yx
∴ (1, 6)Q …………………(1 分)
设直线 BQ: ( 0)y kx b k
40
6
kb
kb
解得 28yx………………………………………………………………(1+1 分)
(0, 8)E……………………………………………………………………(1 分)
(2) 1 2 3 4 5 6
16 8 4 8(0,2) , (0,8) , (4,2) , (4,8) , ( , ) , ( , )5 5 5 5C C C C C C (6 分)
(
图
八
)
E
O
D
A
B C
25.(本题满分 14 分第(1)小题 4 分,第(2)小题 4 分,第(2)小题 6 分)
解:(1)作 BH⊥AC 于点 H(如图一),
∵在 Rt△ABH 中,cos∠A=
5
4 ,AB=15,
∴AH=12………………………………………………(1 分)
∴BH=9.………………………………………………(1 分)
∵AC=15
∴CH=3.………………………………………………(1 分)
∵BC2=BH2+CH2,∴BC2=92+32=90,∴BC=3 10 .…(1 分)
(2)作 OE⊥AB 于点 E,OF⊥AC 于点 F(如图一),
∵点 O 是 BC 的中点,∴OE=OF=
2
1 BH=
2
9 .
∵AM=2MB,AB=AC=15,∴AM=10,BM=5.
∵PA=x,∴PC=15-x,
∴y = S△ABC-S△BOM-S△COP= BH·AC― OE·BM― OF·PC
= ×9×15- × ×5- × ×(15-x)…………………(1+1 分)
=
4
9 x+ 45
2
.…………………………………(1 分)
定义域:(0<x≤15). …………………………… (1 分)
(3)①当 PN⊥AC 时(如图二),作 MG⊥AC 于点 G,
∵在 Rt△AMG 中,cos∠A= ,AM=10
∴AG=8,∴MG=6.
①若点 P1 在 AG 上,由折叠知:∠AP1M=135°,∴∠MP1G=45°.
∵MG⊥AC,∴P1G=MG=6,………(1 分)∴AP1=AG-P1G=2.…………(1 分)
②若点 P2 在 CG 上,由折叠知:∠AP2M=45°.
∵MG⊥AC,∴P2G=MG=6,∴AP2=AG+P2G=14.…………(2 分)
③当 MN⊥AC 时(如图三),
由折叠知:∠AMP3=∠NMP3,P3N3=AP3=x,MN3=MA=10,
∴P3G=8-x,GN3=4.
∵P3N3
2=P3G2+GN3
2,∴x2=(8-x)2+42,∴x=5.……(2 分)
综上所述,x=2 或 5 或 14 时满足△MPN 的一条边与 AC 垂直.
E
H
F
(
图
一
)
C O
P
B
A
M
(
图
二
)
G
N1
C
P1
B
A
M
P2
N2
(
图
三
)
N3
C
P3
B
A
M G
2012 学年嘉定区九年级第一次质量调研
数学试卷
一、选择题:(本大题共 6 题,每题 4 分,满分 24 分)
1. 对于线段 a 、b ,如果 3:2: ba ,那么下列四个选项一定正确的是( )
(A) ba 32 ; (B) 1 ab ; (C)
3
2
3
2
b
a ; (D)
2
5
b
ba .
2. 如图 1,在直角坐标平面内有一点 )4,3(P ,那么射线OP 与 x 轴正半轴的
夹角 的余弦值是( )
(A)
3
4 ; (B)
3
5 ; (C)
5
3 ; (D)
5
4 .
3. 已知抛物线 cbxxy 2 如图 2 所示,那么b 、c 的取值范围是( )
(A) 0b , 0c ; (B) , 0c ;
(C) 0b , ; (D) , 0c .
4.下列四个命题中,真命题的个数为( )
①面积相等的两个直角三角形相似;
②周长相等的两个直角三角形相似;
③有一个锐角相等的两个直角三角形相似;
④斜边和直角边对应成比例的两个直角三角形相似.
(A) 4 ; (B)3 ; (C) 2 ; (D)1.
5.正多边形的一个内角的度数不可能是( )
(A) 80 ; (B) 135 ; (C) 144 ; (D) 150 .
6. 已知⊙ 1O 的半径长为 2 ,若⊙ 2O ( 与 不重合)上的点 P 满足 21 PO ,则下列位置关系中,⊙
1O 与⊙ 2O 不可能存在的位置关系是( )
(A)相交; (B)内切; (C)外切; (D)外离.
二、填空题(本大题共 12 题,每题 4 分,满分 48 分)
7. 如图 3,在△ABC 中, DE ∥ BC , DE 与边 AB 相交于点 D ,与边 AC
相交于点 E ,如果 6AD , 8BD , 4AE ,那么CE 的长为 .
8. 已知 2a , 4b
,且b
与 a 反向,如果用向量b
表示向量 a ,那么 = .
9. 如图 4,飞机 P 在目标 A 的正上方1000米处.如果飞行员测得目标 B 的俯角
为 30 ,那么地面目标 、 之间的距离为 米(结果保留根号).
图 1
y
x O
P
x
y
O
图 2
A
B C 图 3
D E
A B
P
图 4
图 5
10.如果二次函数 13 2 mxxy 的图像经过原点,那么 m 的值为 .
11.二次函数 cxy 22 的图像在 y 轴左侧的部分是 的.(从“上升”或“下降”中选择).
12.二次函数 xxy 42 图像的对称轴是直线 .
13.把抛物线 2( 1) 4yx 先向右平移 3 个单位,再向下平移 2 个单位,所得抛物线的顶点坐标是 .
14.已知⊙O 的半径长为 2 ,点 P 满足 2PO ,那么过点 的直线l 与⊙
不可能存在的位置关系是 (从“相交”、“相切”、“相离”中选择).
15.正六边形的边心距与半径长的比值为 .
16.对于平面图形 A ,如果存在一个圆,使图形 A 上的任意一点到圆心的距离都不大于这个圆的半径,则称
图形 被这个圆“覆盖”.例如图 5 中的三角形被一个圆“覆盖”.如果边长为1的正六边形被一个半径
长为 R 的圆“覆盖”,那么 R 的取值范围为 .
17.如图 6,已知⊙ 1O 与⊙ 2O 相交于点 A 、 B , 8AB , 121 OO ,⊙ 1O 的半径长为5 ,那么⊙ 2O 的
半径长为 .
18.如图 7,弧 EF 所在的⊙O 的半径长为5 ,正三角形 ABC 的顶点 A 、B 分别在半径OE 、OF 上,点C
在弧 上, 60EOF .如果 OFAB ,那么这个正三角形的边长为 .
三、简答题(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
计算:
tan45cos452
60cos45sin30cos60cot .
A
B
C
O F
图 7
E
图 6
A
B
1O 2O
20.(本题满分 10 分)
如图 8,已知△ABC 中, 10 ACAB , 16BC ,矩形
DEFG 的边 EF 在△ABC 的边 BC 上,顶点 D 、G 分别在
边 AB 、 AC 上,设 DE 的长为 x ,矩形 的面积为 y .
求 y 关于 的函数关系式,并写出这个函数的定义域.
21.(本题满分 10 分,第(1)小题 5 分,第(2)小题 5 分)
如图 9,已知点 D 、 E 分别在△ABC 的边 AB 和 AC 上, DE ∥ BC , DBAD 2
1 ,四边形 DBCE
的面积等于16.
(1)求△ABC 的面积;
(2)如果向量 aAD ,向量 bAE
,请用 a 、b
表示向量 BC .
22.(本题满分 10 分,第(1)小题 6 分,第(2)小题 4 分)
如图 10,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O 到球心的长度OG 为50 厘米,小
球在左、右两个最高位置时(不考虑阻力等其他因素),细绳相应所成的角为 90 .
(1)求小球在最高位置和最低位置时的高度差;
(2)联结 EG ,求 OGE 的余切值.
A
B C
D
E F
G
图 8
A
B C
D E
图 9
O
E F
G
图 10
23.(本题满分 12 分,第(1)小题 6 分,第(2)小题 6 分)
已知:点 D 是 Rt ABC△ 的 BC 边的一个动点(如图 11),过点 作 ABDE ,垂足为 E ,点 F 在 AB
边上(点 与点 B 不重合),且满足 BEFE ,联结CF 、 DF .
(1)当 DF 平分 CFB 时,求证:
FB
BD
CB
CF ;
(2)若 10AB ,
4
3tan B .当 CFDF 时,求 BD 的长.
24.( 本题满分 12 分,每小题满分 4 分)
在平面直角坐标系 xOy 中(图 12),已知抛物线 caxaxy 42 ( 0a )经过 )4,0(A 、 (-3,1)B 两
点,顶点为C .
(1)求该抛物线的表达式及点 的坐标;
(2)将(1)中求得的抛物线沿 y 轴向上平移 m( 0m )个单位,所得新抛物线与 y 轴的交点记为点 D .
当△ ACD 是 等腰三角形时,求点 的坐标;
(3)若点 P 在(1)中求得的抛物线的对称轴上,联结 PO ,将线段 绕点 P 逆时针旋转 90 得到线段
OP ,若点O恰好落在(1)中求得的抛物线上,求点 的坐标.
A B
C
D
E F 图 11 A B
C
备用图
O
y
1 x 2 4 3 5 6 -6 -5 -3 -4
3
-2
5
-1
4
5
6
7
8
9
-1
-2
5 图 12
3
2
1
10
25.(本题满分 14 分,第(1)小题 4 分,第(2)、( 3)小题各 5 分)
已知点 A 、B 、C 是半径长为 2 的半圆O 上的三个点,其中点 A 是弧 BC 的中点(如图 13),联结 AB 、
AC ,点 D 、 E 分别在弦 AB 、 AC 上,且满足 CEAD ,联结OD、OE .
(1)求证: OEOD ;
(2)联结 BC ,当 22BC 时,求 DOE 的度数;
(3)若 120BAC ,当点 在弦 AB 上运动时,四边形 ADOE 的面积是否变化?若变化,请简述理由;
若不变化,请求出四边形 的面积.
B
O
A
D
E
图 13
C
O
备用图
O
备用图
2012 学年嘉定区九年级第一次质量调研
数学试卷答案要点与评分标准
说 明:
1.解答只列出试题的一种或几种解法.如果学生的解法与所列解法不同,可参照解答中评分标准相应评分;
2.第一、二大题若无特殊说明,每题评分只有满分或零分;答案若为分数,需要化成最简分数.
3.第三大题中各题右端所注分数,表示学生正确解答到这一步应得分数;
4.评阅试卷,要坚持每题评阅到底,不能因学生解答中出现错误而中断对本题的评阅.如果学生的解答在某
一步出现错误,影响后继部分而未改变本题解答的实质,视影响的程度决定后继部分的给分,但原则上
不超过后继部分应得分数的一半;
5.评分时,给分或扣分均以 1 分为基本单位.
一、选择题:(本大题共 6 题,每题 4 分,满分 24 分)
1.C; 2.C; 3.B; 4.C; 5.A; 6.D.
二、填空题(本大题共 12 题,每题 4 分,满分 48 分)
7.
3
16 (或者
3
15 ); 8. ba
2
1 ; 9. 31000 ; 10. 1m ;
11.下降; 12. 2x ; 13.(4,2); 14.相离;
15.
2
3 ; 16. 1R ; 17. 52 ; 18. 217
5 .
三、简答题(本大题共 7 题,满分 78 分)
19.解:
tan45cos452
60cos45sin30cos60cot =
12
22
2
1
2
2
2
3
3
3
…………(6 分)
22)223(2
1
2
1
)12(2
12
2
1
.……………………………(2+1+1)分
20.解:过点 A 作 BCAH ,交 BC 于 H ,交 DG 于 P (如图 8).…………(1 分)
∵四边形 DEFG , EF 在 BC 边上,
∴ DG ∥ .…………………………………………………………………(1 分)
得 △ADG∽△ABC.………………………………………………………(1 分)
∵ ∥ , BCAH ,∴ DGAP .
∴
BC
DG
AH
AP .……………………………………………………………(1 分)
在△ABC 中,∵ ACAB , BCAH , 16BC ,∴ 82
1 BCBH .
6810 2222 BHABAH .…………………………………(1 分)
∵ BCPH , BCDE ,∴ PH ∥ DE .
又 DG ∥ BC , ∴ DEPH .∴ xPHAHAP 6 .…(1 分)
由 xAP 6 , 6AH , 得
166
6 DGx .…………(1 分)
解得 )6(3
8 xDG .……(1 分)
∴ 2
3
816)6(3
8 xxxxy .……(1 分)
定义域为 60 x .…………………………………………………………(1 分)
21.解:(1)∵ DE ∥ BC ,∴△ADE∽△ABC.∴ 2)( AB
AD
S
S
ABC
ADE
.………(1+1 分)
∵ DBAD 2
1 ,∴ ABAD 3
1 . ∴
9
1
ABC
ADE
S
S .…………………………(1 分)
又∵ 16DBCES四边形 ,∴
9
1
16
ADE
ADE
S
S .解得 2ADES .………………(1 分)
∴ 18216 ABCS .………………………………………………………(1 分)
(2)∵向量 aAD ,向量 bAE
,∴向量 abDE
.…………………(1 分)
∵ ∥ ,∴
AB
AD
BC
DE .………………………………………………(1 分)
∵ ,∴ DEBC 3 .………………………… … ……………(1 分)
∴ 向量 ababBC
33)(3 .………………… ……… ……………(2 分)
22.解:(1)过点 E 作 OGEH ,垂足为点 H . ……………(1 分)
小球在最高位置和最低位置时的高度差就是GH 的长.
根据题意,可知 452
1 EOFEOH .………(1 分)
在 EOH△Rt 中,∵
OE
OHEOH cos ,
∴ 22545cos50cos EOHOEOH . …… (2 分)
A
B C
D
E F
G
图 8
P
H
O
E F
G
H
∴ 22550 OHOGGH .……………(2 分)
(2)联结 EG .……………………………………(1 分)
在 EOH△Rt 中, 22545sin OEEH …(1 分)
∴ 12
225
22550cot EH
GHOGE .…(2 分)
23.解:(1)∵ ABDE , BEFE ,
∴ DBDF , BDFE .………………………………(1 分)
∵ DF 平分 CFB ,∴ BFDCFD .
∵ ,∴ BCFD . …… …………(1 分)
又∵ FCBDCF ,∴△DCF∽△FCB. ………………(1 分)
∴
FB
DF
CB
CF .……………………(2 分)
∵ ,∴
FB
DB
CB
CF . …(1 分)
(2)在 Rt ABC△ 中,由 10AB ,
4
3tan B ,
易得
5
3sin B ,
5
4cos B , 6AC , 8BC .………………………(1 分)
过点C 作 ABCH ,垂足为 H (如图 11-2).
在 Rt△BCH 中,
5
24
5
38sin BBCCH .………………………(1 分)
5
32
5
48cos BBCBH .
设 xBD 5 (备注:也可以设 xBD ),
在 Rt△BDE 中, xxBBDDE 35
35sin , xxBBDBE 45
45cos .
由 xBEEF 4 ,可得 xBFBHHF 85
32 . …………………(1 分)
由 CFDF ,易得 90CFHDFE ,
又 90CFHFCH ,∴ DFEFCH .
方法 1:∴ DFEFCH tantan .………………………………………(1 分)
∵
3
54tan x
CH
FHFCH ,
4
3tantan BDFE ,
∴
4
3
3
54 x . …………………………(1 分)
解得
4
75 x .即
4
7BD .………………(1 分)
方法 2:∴△HCF∽△EFD. ………(1 分)
∴
EF
CH
ED
HF .
A B
C
D
E F 图 11
A B
C
图 11-2
F H
D
E
将 xHF 85
32 , xDE 3 , xEF 4 ,
5
24CH 代入上式,得
xx
x
4
5
24
3
85
32
. ……………………………………………………………………(1 分)
解得
4
75 x .即
4
7BD .………………………………………………………(1 分)
24.解:(1)由抛物线 caxaxy 42 经过 )4,0(A , (-3,1)B ,
得
.1129
,4
caa
c ……………………………(1 分)
解这个方程组,得
.1
,4
a
c
……………………………………………………(1 分)
因此,所求的抛物线的表达式为 442 xxy .…………………………………(1 分)
由 22 )2(44 xxxy ,易得顶点C 的坐标为( 2 ,0 ).…………(1 分)
(2)因为点 D 是将抛物线 442 xxy 沿 y 轴向上
平移 m ( 0m )个单位所得新抛物线与 轴的交点.
所以,点 D 必定在点 A 的上方(如图 12-1),
得 90AOCDAC .…………………(1 分)
∵△ACD 是 等腰三角形,∴ ACAD …(1 分)
在 Rt△AOC 中, 2OC , 4OA ,由勾股定理可得
5242 2222 OAOCAC .
∴ 52 ACAD , 524 ADOAOD .…(1 分)
∴点 D 的坐标为(0 , 524 ).……………………(1 分)
(3)因为点 P 在抛物线 2)2( xy 的对称轴上,故
可设点 P 的坐标为( 2 , n ).
由题意知: OPPO , 90OOP .
过点O作 CPEO ,垂足为 E .
∵ 90OPCPEO , 90OPCPOC .
∴ POCPEO .
∵ 90PCOEPO , ,
,∴△ PEO ≌△ POC .
∴ PCEO , OCPE .
当点 在第二象限时(如图 12-2),
O
y
1 x 2 4 3 5 6 -6 -5 -3 -4
3
-2
5
-1
4
5
6
7
8
9
-1
-2
5 图 12-1
3
2
1
10
A
C
D
nPCEO , 2 OCPE , nEC 2 .
故而可得点O的坐标为( 2n , 2n ).……(1 分)
备注:若点O在第一象限,其坐标也是( , ),下同.
∵点 ( , )恰好在 2)2( xy 上,∴ 2)22( 2 nn .
整理,得 022 nn .解得 21 n , 12 n (舍去).
故可得点 P ( 2 , 2 ).……………………………(1 分)
当点 P 在第三象限时(如图 12-3),
nPCEO , , .
由此可得点 的坐标为( 2n , )……(1 分)
∵ ( 2n , )在抛物线 上,
∴ .
整理,得 ,解得 (舍去), .
故而可知 ( , 1 ). ………(1 分)
25.解:(1)方法 1:联结OA、OB 、OC (如图 13-1),易得 OCOAOB .
在⊙O 中,∵ ,∴ ACAB .…………………… ……(1 分)
∵ OCOB , OAOA , ,∴△AOB≌△AOC.
∴ CAOBAO . ………………………………………………(1 分)
又 ∵ OCOA ,∴ OCACAO .
∴ OCABAO .
∵ CEAD , OCABAO , ,
∴△AOD≌△COE.…………………………………………(1 分)
∴ OEOD . ……………………………………………………(1 分)
方法 2:在⊙ 中,∵ ,∴ . …………………(1 分)
过点O 分别作 ABOM , ACON ,垂足分别为 M 、 N (如图 13-2),
图 12-2
x
y
图 12-3
x
y
∵ ABOM , ACON ,∴ ABAM 2
1 , ACCN 2
1 .
由 ACAB 易得 ONOM , CNAM .……………………(1 分)
∵ CEAD , ,∴ CNCEAMAD ,即 ENDM .
∵ , 90ONEOMD , ,
∴△ODM≌△OEN. ……………………………………………………(1 分)
∴ OEOD . ……………………………………………………………(1 分)
(2)如图 13-3,在△BOC 中,由 2 OCOB , 22BC ,得
822 2222 OCOB , 8)22( 22 BC .
∴ 222 BCOCOB . ∴ 90BOC . ………(1+1 分)
∵ ,O 是圆心,
∴ 45902
1
2
1 BOCAOBAOC . ………………………………(1 分)
∵△AOD≌△COE,∴ COEAOD .………………………………………(1 分)
∴ 45AOCAOECOEAOEAODDOE .……………(1 分)
若使用锐角三角比或其他方法,请参照评分.
(3)当点 D 在弦 AB 上运动时,四边形 ADOE的面积不变.理由如下:…………(1 分)
∵ CAOBAO , 120BAC
∴ 601202
1
2
1 BACCAO ,……………(1 分)
又∵ OCOA ,∴△AOC 是等边三角形.
∴ 2 OCAC .…………………………………………(1 分)
由(1)中的△AOD≌△COE,可知 COEAOD SS .
∴ AOCAOECOEAOEAODADOE SSSSSS 四边形 .……(1 分)
过点O 作 ACON ,垂足为 N ,易得 360sin OAON ,
∴ 3322
1
2
1 ONACS ACD . …………………(1 分)
B
O
A
D
E
图 13-1
C
B
O
A
D
E
图 13-2
C N M
B O
A
D
E
图 13-3
C
B
O
A
D
E
图 13-4
C
第 4 题图
A B
C D
E F
虹口区 2012 学年度第一学期初三年级数学学科
期终教学质量监控测试卷
(满分 150 分,考试时间 100 分钟) 2013.1
考生注意:
1.本试卷含三个大题,共 25 题;
2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题:(本大题共 6 题,每题 4 分,满分 24 分)
[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]
1.抛物线 221yx 的顶点坐标是
A.(2,1) ; B.(-2,1) ; C.(2,-1); D.(-2,-1).
2.关于二次函数 2y ax bx的图像如图所示,下列说法中,正确的是
A.a>0,b>0; B.a>0,b<0;
C.a<0,b>0; D.a<0,b<0.
3.小丽在楼上点 A 处看到楼下点 B 处的小明的俯角是 35°,那么点 B 处的小明看点 A 处的小丽的仰角的
度数是
A.35°; B.45°; C.55°; D.65°.
4.如图,已知 AB∥CD∥EF,BD:DF=2:3,那么下列结论中,正确的是
A. : 2 : 5CD EF ; B. : 2 : 5AB CD ;C. : 2 : 5AC AE ; D. : 2 : 5CE EA .
5. 在△ABC 中,AB=AC=2,∠B = 30°, 那么 BC 等于
A.1; B.2; C. 3 ; D.23.
6. 如图,在△ABC 中,BD=2CD, aBA , bBC ,那么 DA 等于
A. 2
3 ab ; B. 2
3ba ; C. 2
3 ba ; D. 2
3ab .
二、填空题:(本大题共 12 题,每题 4 分,满分 48 分)
[请将结果直接填入答题纸的相应位置]
7.已知线段 b 是线段 a、c 的比例中项,且 a=9,b=6,那么 c= ▲ .
8. 在 Rt△ABC 中,∠C = 90°,AC=3,BC=4,则sin B = ▲ .
9.在 Rt△ABC 中,∠C = 90°, 12cos 13A ,则 tan A = ▲ .
10.如图,已知梯形 ABCD 中,AD∥BC,∠B=30°,∠C=60°,
AD=4,AB=33,则下底 BC 的长= ▲ .
第 6 题图
B
A
C D
60°30°
D
CB
A
第 10 题图
O x
第 2 题图
y
第 17 题图
A
B C
D
E
第 18 题图
11. 若抛物线 2(2 1)y k x x 的开口向下,则 k 的取值范围是 ▲ .
12.请写出一个开口向上,且对称轴为直线 1x 的抛物线的表达式是 ▲ .
13.用配方法把二次函数解析式 2 67y x x 化为 2()y a x m k 的形式是 ▲ .
14.如果抛物线 2( 2) 1yx 经过点 11,Ay 和 21,By,那么 1y 与 2y 的大小关系是
▲ .(填写“>”或“<”或“=”)
15.如图,□ABCD 中,E 是 CD 的延长线上一点,BE 与 AD 交于点 F,CD=2DE.若△DEF 的面积为 a,
则□ABCD 的面积为 ▲ .(用含 a 的代数式表示)
16.在△ABC 中,∠C = 90°,BC=12,点 G 为重心,且 GD⊥BC,那么 CD = ▲ .
17.如图,小明用直角三角形工具测量树的高度 AB.测量时,他使斜边 DF 保持水平,并使 DE 与点 B 在
同一直线上.已知两条直角边 DE = 0.3m,EF = 0.15m,测得边 DF 离地面的高度AC = 1.5m,CD = 17m,
则树高 AB = ▲ m.
18.如图,将△ABE 翻折,使点 B 与 AE 边上的点 D 重合,
折痕为 AC.若 AB=AC=5,AE=9,则 CE= ▲ .
三、解答题(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
计算: 12sin 60 cot 30 2tan 45 tan 60
.
20.(本题满分 10 分)
已知一个二次函数的图像经过 A(1,3)、 B(-1,7)、 C(0,4)三点.求这个二次函数的解析式,并
写出该函数图像的对称轴和顶点的坐标.
A
D B C
第 16 题图
G
A D
B C
第 15 题图
E
F
i
i
20°
9米
6米
B1层
底层 小心碰头A
B
F
CD
E
21.(本题满分 10 分)
如图,点 D、E 分别在线段 AB 和 AC 上,BE 与 CD 相交于点 O, AD AB AE AC ,DF∥AC.
求证:△DOF∽△DOB.
22.(本题满分 10 分,第(1)小题满分 5 分,第(2)小题满分 5 分)
某大型购物中心为方便顾客地铁换乘,准备在底层至 B1 层之间安装电梯 . 截面图如图所示,底层与
B1 层平行,层高 AD 为 9 米,A、B 间的距离为 6 米,∠ACD=20°.
(1)请问身高 1.9 米的人在竖直站立的情况下搭乘电梯,在 B 处会不会碰到头部?请说明理由.
(2)若采取中段平台设计(如图虚线所示).已知平台 EF//DC,且 AE 段和 FC 段的坡度 i=1:2,求平台
EF 的长度.
(参考数据:sin20°取 0.34,cos20°取 0.94,tan20°取 0.36)
第 22 题图
A
B
C
D
O E
F
第 21 题图
D
C
A
E
F
B
第 23 题图
23.(本题满分 12 分,第(1)小题满分 6 分,第(2)小题满分 6 分)
如图,在△ABC 中,BD 平分∠ABC,EF 垂直平分 BD 交 CA 延长线于点 E.
(1)求证: 2ED EA EC;
(2)若 ED=6,BD= CD=3,求 BC 的长.
24.(本题满分 12 分,第(1)小题满分 6 分,第(2)小题满分 6 分)
在△ABC 中,CA=CB, BD 为 AC 边上的高.
(1)如图 1,过点 C 作 CE⊥AB 交 BD 于点 F,交 AB 于点 E,若 BC=5,BD=3,求 BE
CF
的值;
(2)如图 2,若点 P 是 BC 边上一动点,过点 P 作 PM⊥AB 交 BD 于点 N,交 AB 于点 M.设 tanxC ,
BMy PN ,求 y 与 x 的函数解析式.
B C
F
D
A
E
第 24 题图 1
B C
D
A
N
M
第 24 题图 2
P
25.(本题满分 14 分,第(1)小题 5 分,第(2)小题 5 分,第(3)小题 4 分)
如图,已知点 A 和点 B(2,1)在抛物线 1 :c 23
2y x bx 上,过点 A 作 AC∥y 轴交 OB 于点 C,
且 1tan
2
OAC.
(1)求b 的值及点 C 的坐标;
(2)将抛物线 1c 沿 y 轴作上下平移,平移后的抛物线 2c 交直线 AB 于点 E 72( , )33
,交
y 轴于点 F.点 D(2,m)为平移后的抛物线 2c 上一点,点 P 为直线 EF 上一点,如果△ACO∽△PDF,求
点 P 的坐标;
(3)将抛物线 1c 与△ACO 同时平移,点 A、C、O 平移后分别记为点 A、C 、O ,
若点 恰好落在线段 AB 上,△ A C O 与△AOB 重叠部分的面积是 3
16
,求平移后的抛物线 3c 的表达式.
O
C
A
B
y
第 25 题图
x O
C
A
B
y
备用图
x
虹口一模参考答案
一、选择题
ABACDD
二、填空题
7、4 8、 3
5
9、 5
12
10、10 11、k< 1
2
12、答案不唯一,如 2( 1)yx
13、 2( 3) 2yx 14、< 15、12a 16、4 17、10 18、6
三、解答题
19、 23
20、 2 24y x x ,对称轴为直线 1x ,顶点坐标为(1,3)
21、先证明△ADC∽△AEB,即可
22、( 1)不会碰到头部;(2)EF 的长度为 7 米
23、( 2) 3 102BC
24、( 1) 3
8
BE
CF ;( 2) 1
2yx
25、( 1) 7
2b ,点 C 坐标为 1(1, )2
;( 2)点 P 坐标为 32( , )23
或 10 2( , )33
;
(3) 23 21528y x x
长宁区 2012 学年第一学期初三数学期终质量
(满分 150 分,考试时间 100 分钟)
2013.1.16
考生注意:
18.本试卷含三个大题,共 25 题;
19.考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
20.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步
骤。
一. 选择题:(本大题共 6 题,每题 4 分,满分 24 分)
【下列各题的四个选项中,有且只有一个选项是符合题目要求的,请把符合题目要求的选项的代号填涂
在答题纸的相应位置上.】
1. 已知△ ABC 中, 90C ,则 cosA 等于( )
A. AB
BC B. AC
BC C. AC
AB D. AB
AC
2. 如图,在平行四边形 ABCD 中,如果 AB a , AD b ,那么 ab 等于( )
A. BD B. AC C. DB D.CA
3. 如图,圆 O 的弦 AB 垂直平分半径 OC,则四边形 OACB 一定是( )
A. 正方形 B.长方形 C. 菱形 D.梯形
4. 已知抛物线 21 ( 5) 33yx ,下列说法正确的是( )
A.开口向下,顶点坐标 (5 3), B.开口向上,顶点坐标
C.开口向下,顶点坐标( 5 3) , D.开口向上,顶点坐标
5. 如图,△ ABC 是等边三角形,被一平行于 BC 的矩形所截(即:FG//BC),若 AB 被截成三等分,则图中阴
影部分的面积是△ ABC 的面积的 ( )
A.
9
1 B.
9
2 C.
3
1 D.
9
4
D C
B A
第 2 题图
E H
F G
C B
A
第 5 题图
第3题图
A. B. C. D.
第 14 题图 第 17 题图 第 12 题图
第 16 题图
6.在同一直角坐标系中,函数 y mx m和函数 2 22y mx x ( m 是常数,且 0m ) 的图像可能..
是 ( )
二.填空题:(本大题共 12 题,每题 4 分,满分 48 分)
【请将结果直接填入答题纸的相应位置】
7.已知实数 x、y 满足
2
3y
x ,则
y
yx
2
2 .
8. 已知,两个相似的△ ABC 与△ DEF 的最短边的长度之比是 3:1,若△ ABC 的周长是 27,则△ DEF 的周长
为 .
9. 已知△ ABC 中,G 是△ ABC 的重心,则
ABC
ABG
S
S .
10. 在直角坐标平面内,抛物线 y =-x2+2x+2 沿 y 轴方向向下平移 3 个单位后,得到新的抛物线解析式
为 .
11.在直角坐标平面内,抛物线 y =-x2+c 在 y 轴 侧图像上升(填“左”或“右”).
12. 正八边形绕其中心至少要旋转 度,就能与原来的图形重合.
13. 已知圆⊙O 的直径为 10,弦 AB 的长度为 8,M 是弦 AB 上一动点,设线段 OM=d,则 d 的取值范围
是 .
14. 如图,某人顺着山坡沿一条直线型的坡道滑雪,当他滑过 130 米长的路程时,他所在位置的竖直高度下
降了 50 米,则该坡道的坡比是 .
15.已知两圆相切,圆心距为 2 cm,其中一个圆的半径是 6 cm,则另一个圆的半径是____ cm.
16.已知△ ABC 中,AB=6,AC=9,D、E 分别是直线 AC 和 AB 上的点,若
AB
AE
AC
AD 且 AD=3,则
BE= .
17. 如图,已知 Rt△ ABC, 90ACB , 30B ,D 是 AB 边上一点,△ ACD 沿 CD 翻折,
A 点恰好落在 BC 边上的 E 点处,则 EDBcot = .
18. 已知,二次函数 f(x) = ax2 + bx + c 的部分对应值如下表,则 f(- 3) = .
E
P
D
CB
A
三、解答题:(本大题共 7 题,第 19--22 题,每题 10 分;第 23、24 题,每题 12 分;25 题 14 分;满分 78 分)
19.计算: 30345
2
45 tan-sintan .
20.如图,在正方形网格中,每一个小正方形的边长都是 1,已知向量 a 和b 的起点、终点都是小正方形的顶
点.请完成下列问题:
(1)设: babam 4
1
2
1
3
1 43 ,
baban 3
2
5
2 635 .
判断向量 nm、是否平行,说明理由;
(2)在正方形网格中画出向量: ab 2
34 ,并写出
的模.(不需写出做法,只要写出哪个向量是所求向量).
21.如图,等腰梯形 ABCD 中,AD//BC,AB=CD,AD=3,BC=7,∠B=45º,
P 在 BC 边上,E 在 CD 边上,∠B=∠APE.
(1)求等腰梯形的高;
(2)求证:△ ABP∽△ PCE.
x -2 -1 0 1 2 3 4 5
y 5 0 -3 -4 -3 0 5 12
D
E
O
A
C B
D
C
M A
B
O
y
x
22.由于连日暴雨导致某路段积水,有一辆卡车驶入该积水路段。如图所示,已知这辆卡车的车轮外直径(包
含轮胎厚度)为 120 cm ,车轮入水部分的弧长约为其周长的
3
1 ,试计算该路段积水深度(假设路面水平).
23. 如图,已知 Rt△ ABC 中, 90CBA ,⊙O 是 Rt△ ABC 的内切圆,其半径为 1,E、D 是切点,
105BOC .
求 AE 的长.
24. 在直角坐标平面中,已知点 A(10,0)和点 D(8,0)。点 C、B 在以 OA 为直径的⊙M 上,且四边形 OCBD 为
平行四边形.
(1)求 C 点坐标;
(2)求过 O、C、B 三点的抛物线解析式,并用配方法求出该抛物线的顶点坐标和对称轴;
(3)判断:(2)中抛物线的顶点与⊙M 的位置关系,说明理由.
Q
C
PB A
25.如图,已知 Rt△ ABC, 90B ,AB=8 cm,BC=6 cm,点 P 从 A 点出发,以 1cm/秒的速度沿 AB 向 B
点匀速运动,点 Q 从 A 点出发,以 x cm/秒的速度沿 AC 向 C 点匀速运动,且 P、Q 两点同时从 A 点出发,
设运动时间为 t 秒( 80 t ),联结 PQ。解答下列问题:
(1)当 P 点运动到 AB 的中点时,若恰好 PQ//BC,求此时 x 的值;
(2)求当 x 为何值时,△ ABC∽△ APQ ;
(3)当△ ABC∽△ APQ 时,将△ APQ 沿 PQ 翻折,A 点落在 A’, 设△ A’PQ 与△ ABC 重叠部分的面积为 S,
写出 S 关于 t 的函数解析式及定义域.
2012 学年第一学期初三数学期终质量调研试卷参考答案
一 .选择题:(本大题共 6 题,每题 4 分,满分 24 分)
1. 填空题:(本大题共 12 题,每题 4 分,满分 48 分)
7、 2 ; 8、9 ; 9、 3
1 ; 10、 122 xxy ; 11、左 ; 12、45 ;13、3 ≤ d ≤ 5;
14、5:12 ;15、4 或 8 ; 16、 4 或 8 ; 17、 3 ;18、12 .
三.解答题:
19(10 分)解:原式= 32
2
2
1 - (6 分)
= 12
2
2
2 - (2 分)
= 12 - (2 分)
20(10 分)解:(1)(6 分)
am (2 分) an 13 (2 分)
m-n 13 mn// (2 分).
(2) (4 分)
图正确 (2 分) 54 2
3 a-b (2 分).
21(10 分)(1)(5 分)
解:作 AF BC 于 F,作 DG BC 于 G. (1 分)
90DGCAFB 且 AF//DG
在△ABF 和△DCG 中
DCAB
CB
DGCAFB
△ABF △DCG
BF=CG
AD//BC 且 AF//DG AFGD 是平行四边形
AD=FG
AD=3,BC=7 BF=2 (2 分)
在 Rt△ABF 中,∠B=45º ∠BAF = 45º
AF=BF =2
1 2 3 4 5 6
D B C A C D
等腰梯形的高为 2. (2 分)
(2)(5 分)
ABCD 是等腰梯形, CB (1 分)
BAPBEPCAPEAPC
又 APEB
EPCBAP (2 分)
在△ABP 和△PCE 中,
EPCBAP
CB
△ABP∽△PCE . (2 分)
22. (10 分)
23. 解:设车轮与地面相切于点 E,联结 OE 与 CD 交于点 F,联结 OC. 设 nCOD (2 分) 弧 CD 等于⊙
O 周长的 3
1 即 dd 3
1
360 n n= 120 (2 分)
据题意得 OE CD 且 OE=OC=OD= 2
1 AB=60 cm
OF 是 COD 的平分线 602
1
2
1 nCODFOD (2 分)
90ODFFOD 30ODF
在 Rt△OFD 中, 30ODOF 2
1 cm (2 分)
FE= OE-OF =30 cm
积水深度 30 cm (2 分)
24. (12 分)
解: 联结 OD、OE. (1 分)
OD=OE=1
O 是△ABC 的内切圆圆心
OB、OC 分别是 ABC、 ACB 的角平分线
即 ABCOBEOBD 2
1 且 ACBOCD 2
1
又 90CBA 45ACBOCD 2
1 (3 分)
OD、OE 是过切点的半径 OD BC 且 OE AB
90CODOCD
45OCDCOD OD=CD=1
105COB 60COD-COBDOB
在 Rt△OBD 中 31 DB
OD
DBBODtan 3DB (4 分)
90BODOBD 30OBD
30ABCOBEDOB 2
1 60ABC
BC=BD+CD=1+ 3
在 Rt△ABC 中 AB=2+2 3
在 Rt△OBE 中 OE=1 30OBE BE = 3 (3 分)
AE= 2+ (1 分)
24.(12 分)
解: (1)(5 分)
联结 CM,作 ME CB 于 E。(1 分)
M 是圆心 CB 是⊙M 的弦 CBEBCE 2
1
OA 是⊙M 的直径 且 A(10,0) OA=10
CM=OM= 2
1 OA=5 且 M(5,0)
D(8,0) OD=8
OCBD 为平行四边形 CB=OD=8
4CBCE 2
1
在 Rt△CME 中 34-5CE-MCME 2222 (3 分)
C(1,3) (1 分)
(2)(5 分)
OCBD 为平行四边形 CB//OA
又 CB=8 B(9,3)
据题意,设抛物线解析式为: )( 0 abxaxy 2
C、B 代入得
381 9ba
3ba 解得
3
10
3
1
b
a
xx-y 2
3
10
3
1 (2 分)
3
252
3
12
3
12
3
1
3
10
3
1 )5()252510()10 xxxxx- xx-y 2 ( (1 分)
顶点坐标(5, 3
25 ) 对称轴直线 x=5 (2 分)
(3)(2 分)设抛物线顶点为 N NM= > 5 (1 分)
顶点 N 在⊙M 外。(1 分)
25(14 分)
三、 (3 分)设 AP= t AQ= xt ( 80 t )
AB=8 AP= 2
1 AB=4 即 t=4 (1 分)
Rt△ABC, 90B ,AB=8 cm,BC=6 cm AC=10 cm (1 分)
PQ//BC AC
AQ
AB
AP 即 10
4
8
4 x 4
5x (1 分)
四、 (4 分) AA
当 AC
AQ
AB
AP 时 108
xtt 4
5x (2 分)
当 AB
AQ
AC
AP 时 810
xtt 5
4x (2 分)
当 或 时△ABC∽△APQ
五、 (7 分)
(有分类讨论思想,得 1 分)
当 时
)8t4()4t(
)4t0
2
2
3
2
8
3 (tS (3 分)
(说明:2 个解析式各 1 分,定义域共 1 分)
当 时
)8t(tt
)t0
4
25
7
600
7
1922
175
342
4
252
25
6 (tS (3 分)
(说明:同上)
2013 年上海市宝山区中考数学一模试卷
(满分 150 分,考试时间 100 分钟) (2013.1)
一、选择题(本大题共 6 题,每题 4 分,满分 24 分)
1、 下列各式中,正确的是 ( )
A.sin20°+sin30°=sin50°; B.Sin60°=2sin30°;
C.tan30°·tan60°=1; D.cos30°<cos60°;
2、下列分式方程去分母后所得结果正确的是( )
A. 11
2
1
1
x
x
x
去分母得, 1)2)(1(1 xxx ;
B. 125
5
52 xx
x 去分母得, 525 xx ;
C.
24
2
2
2
2
x
x
x
x
x
x 去分母得, )2(2)2( 2 xxxx ;
D.
1
1
3
2
xx
去分母得, 3)1(2 xx ;
3、已知关于 x 的方程 022 kxx 没有实数根,则 k 的取值范围是( )
A. 1k B. 1k C. 1k D. 1k
4、下列命题正确是( )
A.长度相等的两个非零向量相等
B.平行向量一定在同一直线上
C.与零向量相等的向量必定是零向量
D.任意两个相等的非零向量的始点与终点是一平行四边形的四顶点
5、如图所示,在△ABC 中,DE∥AB∥FG,且 FG 到 DE,AB 的距离之比为
1:2,若△ABC 的面积为 32,△CDE 的面积为 2,则△CFG 的面积等于 ( )
A.6 B.8 C.10 D.12
6、一次函数 baxy 与二次函数 cbxaxy 2 在同一坐标系中的图像可能是( )
A B C D
二、填空题(本大题共 12 题,每题 4 分,满分 48 分)
7、使 3x 有意义的 x 的取值范围是_____________.
8、不等式组
01
032
x
x 的解集是_________________.
9、分解因式 baaba 332 =________________.
10、关于 x 的一元二次方程 04)2( 22 kxxk 的一个根为 0,则 k 的值是__________.
11、在平面直角坐标系中。把抛物线 12 2 xy 的图像向左平移 2 个单位,所得抛物线的解析式为
_____________.
12、已知代拿 A(x1,y1),B(x2,y2)在函数 1)1( 2 xy 的图像上,若 x1>x2>1,则 y1_____y2.
13、在平面直角坐标系中,点 A 是抛物线 kxay 2)3( 与 y 轴的交点,点 B 是这条抛物线上得另一点,
且 AB∥x 轴,则以 AB 为边的等边三角形的周长为____________
14、如图,正方形 ABCD 中,M 是边 BC 上一点,且 BM=
4
1 BC,若 aAB ,
bAD ,则 DM _______(用 a 和b 表示)
15、某坡面的坡度为 1:
3
3 ,则坡角是_________度
16、如图,菱形 ABCD 中,点 E、F 在对角线 BD 上,BE=DF=
6
1 BD,
若四边形 AECF 为正方形,则 tan∠ABE=______________
17、在实验中我们常常采用利用计算机在平面直角坐标系中画出抛物线
2xy 和直线 y=-x+3,利用两图像交点的横坐标来求一元二次方程
032 xx 的解,也可以在平面直角坐标系中画出抛物线 32 xy 和直线 y=-x,用它们交点的横坐标
来求该方程的解。所以求方程 036 2 xx
的近似解也可以利用熟悉的函数_________和__________的图
像交点的横坐标来求得。
18、如图在平面直角坐标系 xOy 中,多边形 OABCDE 的顶点坐标为 O(0,0), A(2,0), B(2,2), C(4,2),
D(4,4), E(0,4),若如图国电 M(1,2)的直线 MP(与 y 轴交于点 P)将多边形 OABCDE 分割成面积相
等的两部分,则直线 MP 的函数表达式是__________
三、(本大题共 8 题,第 19-22 题每题 8 分,第 23、24 题每题 10 分,第 25 题 12 分,第 26 题 14 分,满分
78 分)
19、计算:
45cos-60sin
45tan)8
1(45sin218)3( 10
20、二次函数 mxxy 22 的图像与 x 轴的一个交点为 A(3,0),另一个交点为 B,且与 y 轴交于点 C
(1)求 m 的值和点 B 的坐标
(2)求△ABC 的面积
21、将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=12,求(1)重叠的
边 DF 的长度
(2)重叠部分四边形 DBCF 的面积
22、在 Rt△ABC 中,∠ACB=90°,CD⊥AB,垂足为 D,E、F 分别是 AC,BC 边上一点,且 CE=
4
1 AC,
BF=
4
1 BC,
(1)求证:
BD
CD
BC
AC
(2)求∠EDF 的度数
23、如图,△ABC 中,∠ACB=90°,CD⊥AB 于点 D,E 是 AC 的中点,DE 的延长线交 BC 的延长线于
点 F,EF=5,∠B 的正切值为
2
1
(1)求证:△BDF∽△DCF;( 2)求 BC 的长
24、在对口扶贫活动中,企业甲将经营状况良好的某消费品专卖店,以 188 万元的优惠价转让给了尚有 120
万无息贷款还没有偿还的小型福利企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月
最低生活费的开支 5.6 万元后,逐步偿还转让费(不计利息),维持乙企业的正常运转每月除职工最低生活
费外,还需其他开支 2.4 万元,从企业甲提供的相关资料中可知这种热门消费品的进价是每件 12 元:月销
售量 Q(万件)与销售单价 P(元)的关系如下表所示:
销售单价 P
(元)
…… 13 14 15 16 17 18 ……
月销量 Q(万
件)
…… 7 6 5 4 3 2 ……
(1) 试确定月销售量 Q(万件)与与销售单价 P(元)之间的函数关系式
(2) 当商品的销售单价为多少元时,扣除各类费用后的月利润余额最大?
(3) 企业乙依靠该店,能否在 3 年内脱贫(偿还所有债务)?
25、在平面直角坐标系中,抛物线过原点 O,且与 x 轴交于另一点 A(A 在 O 右侧),顶点为 B。艾思轲同
学用一把宽 3cm 的矩形直尺对抛物线进行如下测量:(1)量得 OA=3cm,( 2)当把直尺的左边与抛物线的
对称抽重合,使得直尺左下端点与抛物线的顶点重合时(如图 1),测得抛物线与直尺右边的交点 C 的刻度
读数为 4.5cm
艾思轲同学将 A 的坐标记作(3,0),然后利用上述结论尝试完成下列各题:
(1)写出抛物线的对称轴
(2)求出该抛物线的解析式
(3)探究抛物线的对称轴上是否存在使△ACD 周长最小的点 D
(4)然后又将图中的直尺(足够长)沿水平方向向右平移到点 A 的右边(如图 2),直尺的两边交 x 轴于
点 H,G,交抛物线于 E,F,探究梯形 EFGH 的面积 S 与线段 EF 的长度是否存在函数关系。
同学:如上述(3)( 4)结论存在,请你帮艾思轲同学一起完成,如上述(3)( 4)结论不存在,请你告诉
艾思轲同学结论不存在的理由
26、已知∠AOB=90°,OM 是∠AOB 的平分线,将一个直角三角板的直角顶点 P 放在射线 OM 上,OP=m
(m 为常数且 m 0),移动直角三角板,两边分别交射线 OA,OB 与点 C,D
(1)如图,当点 C、D 都不与点 O 重合时,求证 PC=PD
(2)联结 CD,交 OM 于 E,设 CD=x,PE=y,求 y 与 x 之间的函数关系式
(3)若三角板的一条直角边与射线 OB 交于点 D,另一直角边与直线 OA,直线 OB 分别交于点 C,F,且
△PDF 与△OCD 相似,求 OD 的长
2013 年上海市宝山区中考数学一模试卷参考答案
一、选择题:C D A C B C
二、填空题:
7. x>3
8. -1
13. 18
14. a-3/4b (a,b 向量符号标上)
15. 60
16. 2/3
17. y=6/x, y=x2-3
18. y=1/2x+3/2
三、解答题:
19. 4√2+2√3-7
20. (1)m=3; B(-1,0)
(2)6
21. 12-4√3; 48√3-60
22. (1) AC/BC=CD/BD(角 ACB=90 度,CD 垂直 AB) (2)角 EDF=90 度
23. (1)证明题省略;(2)BC=12
24. (1) Q=20-P
(2)16 元,最大利润
(3) 不能
25. (1)直线=3/2
(2)y=1/2x2-3/2x
(3)D(3/2,9/8)
(4)设点 E 横坐标为 a, 则 S=3/2a2 EF=3√1+a2 S=(EF2-9)/6
26. (1)过 P 作 PF 垂直于 AO,PG 垂直于 OB,因为 OM 平分角 AOB,所以 PF=PG,易证三角形 PFC
全等于三角形 PGD,所以 PC=PD;
(2)y=(1/2m)x2
(3)1. OD=m ;2. OD=√3 m
金山区 2012 学年第一学期数学期末质量抽查
(满分 150 分,考试时间 100 分钟)
考生注意:
1、本试卷含四个大题,共 25 题;
2、答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律
无效;
3、除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计
算的主要步骤。
一、选择题(本大题共 6 题,每题 4 分,满分 24 分)
1、把抛物线 22( 1) 1yx 向左平移一个单位,所得到的抛物线解析式为( )
A、 22( 2) 1yx B、 221yx C、 22( 1) 2yx D、 22( 1)yx
2、比例尺为1:500000的地图上,A、B 两点的距离为 30 厘米,那么 A、B 两地的实际距离是
( )
A、5000 米 B、50 千米 C、150 千米 D、15 千米
3、在 Rt△ABC 中,∠C=90°,BC=3,AC=4,那么∠A 的正弦值是( )
A、 3
4 B、 4
3 C、 3
5 D、 4
5
4、如图,已知在△ABC 中,G 是△ABC 的重心,GE∥BC,BC=8,
那么 GE 的长度为( )
A、 B、2 C、 8
3 D、16
3
5、在下列正多边形中,中心角的度数等于它的一个内角的度数的是( )
A、正三边形 B、正四边形 C、正五边形 D、正六边形
6、已知 O 的半径等于 5,点 A、B 到圆心的距离分别是 6、5,那么直线 AB 与 O 的位置关
系是( )
A、相离 B、相切 C、相交 D、相切或相交
A
B C D
E G
第 4 题
二、填空题(本大题共 12 小题,每题 4 分,满分 48 分)
7、计算:5 3( 2 )a a b __________________。
8、抛物线 22( 1) 3yx 的顶点坐标是___________________。
9、已知抛物线 2 3y x bx 经过点(1,2) 那么抛物线的解析式是_____________________。
10、已知函数 2 1( 1) 3ay a x x 是二次函数,那么 a=__________。
11、已知 3
2
xy
y
,那么 3
2
xy
xy
_____________。
12、如图,已知 DE∥BC, 9ADES ,AD=3,BD=2,那么 ABCS _________。
13、在 Rt△ABC 中,∠C=90°, 3sin 5A ,那么 tan B ________。
14、如图,点 P 是直线 3
2yx 在第一象限上一点,那么cot POx_________。
15、已知 A与 B 外切, 的半径为 5cm,圆心距 AB 为 7cm,那么 B 的半径为____cm。
16、如图,已知 AC⊥BC,斜坡 AB 的坡比为1: 3 ,BC=30 米,那么 AC 的高度为_____米。
17、如图,已知四边形 ABCD 是平行四边形,延长 BC 至 E,联结 AE 交 CD 于 F,AD=2,
AB=4,BE=3,那么 DF=_________。
18、已知在等腰直角三角形 ABC 中,∠BAC=90°,AB=AC=4,将边 AB 绕着点 A 旋转至 'AB
位置,且 'AB 与 AC 边之间的夹角为 30°,那么线段 'BB 的长等于_______。
三、解答题(本大题共 7 小题,满分 78 分)
19、计算:
2
2
cos 30 sin 45 cos45 tan60
sin 30 tan 45 cot30 cot60
A
B C
D E
第 12 题
第 17 题
F
A
B
C
D
E
A
B C
第 16 题
P .
x
y
O
第 14 题
20、已知二次函数 2y ax bx c (a≠0),列表如下:
x …… 1 1
2 0 1
2
1 112
2 ……
y …… 2 3
4
0 1
4 0 3
4
2 ……
(1)根据表格所提供的数据,请你写出顶点坐标___________,对称轴__________。
(2)求出二次函数解析式。
21、如图,为了测量一颗被风吹斜了的大树的高度,某人从大树底部 B 处往前走 20 米到 C 处,
用测角器测得树顶 A 的仰角为 30°,已知测角器的高 CD 为 1 米,大树与地面成 45°的夹角
(平面 ABCD 垂直于地面),求大树的高(保留根号)。
22、如图,CD 是半圆 O 的一条弦,CD∥AB,延长 OA、OB 至 F、E,使 1
2AF BE,联结
FC、ED,CD=2,AB=6。
(1)求∠F 的正切值;
(2)联结 DF,与半径 OC 交于 H,求△FHO 的面积。
B F O
.
A
C D
E
第 22 题
A
B C
D
第 21 题
23、如图,已知 1O 与 2O 相交于点 E、F,点 P 是两圆连心线上的一点,分别联结 PE、PF
交 2O 于 A、C 两点,并延长交 与 B、D 两点。
求证:PA=PC。
24 、如图,已知 C 的圆心在 x 轴上,且经过 (1,0)A 、 ( 3,0)B 两点,抛物线 2y mx bx c (m
>0)经过 A、B 两点,顶点为 P。
(1)求抛物线与 y 轴的交点 D 的坐标(用 m 的代数式表示);
(2)当 m 为何值时,直线 PD 与圆 C 相切?
(2)联结 PB、PD、BD,当 m=1 时,求∠BPD 的正切值。
C.
A B
D
P
O
x
y
第 24 题
A
B
C
D
E
F
P
第 23 题
25、如图,已知 90ABM ,AB=AC,过点 A 作 AG⊥BC,垂足为 G,延长 AG 交 BM 于 D,
过点 A 做 AN∥BM,过点 C 作 EF∥AD,与射线 AN、BM 分别相交于点 F、E。
(1)求证:△BCE∽△AGC
(2)点 P 是射线 AD 上的一个动点,设 AP=x,四边形 ACEP 的面积是 y,若 AF=5, 25
3AD 。
①求 y 关于 x 的函数关系式,并写出定义域;
②当点 P 在射线 AD 上运动时,是否存在这样的点 P,使得△CPE 的周长为最小?若存
在,求出此时 y 的值,若不存在,请说明理由。
A
B
C
D E
F
G
M
N
第 25 题
金山区一模参考答案
一、选择题
BCCCBD
二、填空题
7、 2 +6ab 8、(1, 3) 9、 2 23y x x 10、 1 11、 1 12、25
13、 4
3
14、 2
3
15、2 16、10 3 17、 8
3
18、4 或43
三、解答题
19、 31
4
20、( 1)顶点坐标为 11( , )24 ,对称轴为直线 1
2x ;( 2) 2y x x
21、 21 3 23
2
米
22、( 1) 22tan 5F ;( 2) 92
2S
23、略
24、( 1)(0, 3 )m ;( 2) 3
3m 时直线与圆相切 ;( 3) tan 3BPD
25、( 2) 12 2yx (x>0);
(3)当点 P 运动到点 D 时,B、P、E 三点共线时,周长最小为 86
3
黄浦区 2012 学年第一学期九年级期终考试数学
(满分 150 分,考试时间 100 分钟) 2013 年 1 月 17 日
考生注意:
1、本试卷含四个大题,共 25 题;
2、答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律
无效;
3、除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计
算的主要步骤。
一、选择题(本大题共 6 题,每题 4 分,满分 24 分)
1、如果△ABC∽△DEF(其中顶点 A、B、C 依次与顶点 D、E、F 对应),那么下列等式中不
一定成立的是( )
A、∠A=∠D B、 AD
BE
C、AB=DE D、 AB DE
AC DF
2、如图,地图上 A 地位于 B 地的正北方,C 地位于 B 地的北偏东 50°方向,且 C 地到 A 地、
B 地距离相等,那么 C 地位于 A 地的( )
A、南偏东 50°方向 B、北偏西 50°方向
C、南偏东 40°方向 D、北偏西 40°方向
3、将抛物线 2yx 向左平移 2 个单位,则所得的抛物线的解析式为( )
A、 2( 2)yx B、 2( 2)yx C、 2 2yx D、 2 2yx
4、如图,△PQR 在边长为 1 个单位的方格纸中,它的顶点在小正方形顶点位置,其中点 A、
B、C、D 也是小正方形的顶点,那么与△PQR 相似的是( )
A、以点 P、Q、A 为顶点的三角形 B、以点 P、Q、B 为顶点的三角形
C、以点 P、Q、C 为顶点的三角形 D、以点 P、Q、D 为顶点的三角形
C
B
A
(第 2 题)
Q
R P
D
C B A
(第 4 题)
A B D
C
(第 6 题)
5、抛物线 2 32y x x 与坐标轴(含 x 轴、y 轴)的公共点的个数是( )
A、0 B、1 C、3 D、3
6、如图,在△ABC 中,∠ACB=90°,CD 为边 AB 上的高,已知 BD=1,则线段 AD 的长是
( )
A、 2sin A B、 2cos A C、 2tan A D、 2cot A
二、填空题(本大题共 12 小题,每题 4 分,满分 48 分)
7、已知 7
4
x
y ,则 xy
xy
的值为__________。
8、计算: 2( ) 3( )a b a b ___________。
9、已知两个相似三角形的周长比为 2:3,且其中较大三角形的面积是 36,那么其中较小三角
形的面积是__________。
10、如图,第一象限内一点 A,已知 OA=5,OA 与 x 轴正半轴说成的夹角为 ,且 tan 2 ,
那么点 A 的坐标是____________。
11、如图,某人沿着一个坡比为1:3的斜坡(AB)向前行走了 10 米,那么他实际上升的垂直
高度是____________米。
12、抛物线 2 23y x x 的顶点坐标是_____________。
13、如果抛物线 2( 2) 3y a x x a 的开口向下,那么 a 的取值范围是____________。
14、若 1x 、 2x 是方程 22 3 4 0xx 的两个根,则 1 2 1 2x x x x 的值为_________。
15、已知二次函数 ()y f x 图像的对称轴是直线 2x ,如果 (3) (4)ff> ,那么 ( 3)f ___ ( 4)f 。
α
y
x O
(第 10 题)
H
B
A
(第 11 题) (第 17 题)
A B
C D
E
(填“>”或“<” )
16、已知点 P 是二次函数 2 24y x x 图像上的点,且它到 y 轴的距离为 2,则点 P 的坐标是
_______________。
17、如图,E 是正方形 ABCD 边 CD 的中点,AE 与 BD 交于点 O,则 tan AOB______。
18、在 Word 的绘图中,可以对画布中的图形进行缩放,如下图 1 中正方形 ABCD(边 AB 水
平放置)的边长为 3,将它在“设置绘图画布格式→大小→缩放”中,高度设定为 75%,
宽度设定为 50%,就可以得到下图 2 中的矩形 EFGH ,其中 11 3 50% 1.5AB ,
11 3 75% 2.25AD ,实际上 word 的内部是在画布上建立了一个以水平线与竖直线为坐
标轴的平面直角坐标系,然后赋予图形的每个点一个坐标 ( , )xy,在执行缩放时,是将每
个点的坐标做变化处理,即由( , )xy变为( %, %)x n y m,其中 %n 与 %m 即为设定宽度与
高度的百分比,最后再由说得点的新坐标生成新图形。
现在画布上有一个△OMN ,其中∠O=90°,MO=NO,且斜边 NM 水平放置(如图
3),对它进行缩放,设置高度为 150%,宽度为 75%,得到新图形为△ 1 1 1O M N (如图 4),
那么 1 1 1cos O M N 的值为__________。
三、解答题(本大题共 7 小题,满分 78 分)
19、计算:
2
2
2sin 60 cos60
cot 30 4cos 45
=>
B A
D
C
图 1
图 2
=>
N M
O
图 3
图 4
20、如图,点 E 是平行四边形 ABCD 边 BC 上一点,且 : 2:1BE ED ,点 F 是边 CD 的中点,
AE 与 BF 交于点 O,
(1)设 ,AB a AD b,试用 a 、b 表示 AE ;
(2)求 :BO OF 的值。
21、已知二次函数的图像经过点(0, 8) 和(3, 5) ,且其对称轴是直线 1x ,求此二次函数的解
析式,并求出次二次函数图像与 x 轴公共点的坐标。
22、如图,在△ABC 中, 90C ,AC=4,BC=6,点 D 是边 BC 上一点,且 CAD B 。
(1)求线段 CD 的长;
(2)求sin BAD 的值。
O
F
E
D
C B
A
D
B C
A
23、如图,点 D 是 Rt△ABC 斜边 AB 上一点,点 E 是直线 AC 左侧一点,且 EC⊥CD,∠EAB
=∠B。
(1)求证:△CDE∽△CBA;
(2)如果点 D 是斜边 AB 中点,且 3tan 2BAC,试求 CDE
CBA
S
S
的值。
( CDES 表示△CDE 的面积, CBAS 表示△CBA 的面积)
24、已知二次函数 2 3y ax bx 的图像与 x 轴交于点 (1,0)A 和点 (3,0)B ,交 y 轴于点 C,其图
像顶点为 D。
(1)求此二次函数的解析式;
(2)是问△ABD 与△BCO 是否相似,并证明你的结论;
(3)若点 P 是此二次函数图像上的点,且 PAB ACB ,试求点 P 的坐标。
O
y
x
A
B C
D E
25、如图,在等腰三角形 ABCD 中,AD∥BC,AD=2,AB=5, 3sin 5B,点 E 是边 BC 上
的一个动点(不与点 B、C 重合)作 AEF AEB ,使边 EF 交边 CD 于点 F(不与点 C、
D 重合),设 ,BE x CF y。
(1)求边 BC 的长;
(2)当△ABE 与△CEF 相似时,求 BE 的长;
(3)求 y 关于 x 的函数关系式,并写出定义域。
F
E C B
D A
C B
D A
(备用图)
黄浦区一模参考答案
一、选择题
CAABDD
二、填空题
7、11
3
8、5ab 9、16 10、( 5,2 5) 11、 10 12、( 1,2)
13、a<2 14、 1
2 15、> 16、(2,4) ,( 2,12) 17、3 18、 5
5
三、解答题
19、3 2 2
20、( 1) 2
3AE a b ;( 2) :BO OF 的值为 1
21、 2 28y x x ,公共点为( 2,0) 与(4,0)
22、( 1) 8
3CD ;( 2) 5sin 13BAD
23、( 2) 13
36
CDE
CBA
S
S
24、( 1) 2 43y x x ;( 2)是相似,利用三边对应成比例来证明;(3) 53( , )24 或 75( , )24
25、( 1) 10BC ;( 2) 43BE 或 10;( 3)
2
2
10 140 400
16 39
xxy xx
(4<x<10)
★浦东新区 2012 学年度第一学期期末质量测试卷:(静安_闵行_浦东_杨浦_松江_青浦等六区合用卷)
共计 11 套试卷