数学理卷·2017届辽宁省本溪市高级中学、大连育明高级中学、大连二十四中高三联合模拟考试（2017 10页

‎ ‎ 数学（理科）试卷 第Ⅰ卷 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.若集合，，且，则的值为（ ）‎ A． B． C．或 D．1或或0‎ ‎2.设（是虚数单位），则的虚部为（ ）‎ A． B． C． D．‎ ‎3.下图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的分别为8，12，则输出的（ ）‎ A．4 B．2 C．0 D．14‎ ‎4.已知函数的图象的一个对称中心是点，则函数的图象的一条对称轴是直线（ ）‎ A． B． C. D．‎ ‎5.已知等差数列的公差，且，，成等比数列，若，为数列的前项和，则的最小值为（ ）‎ A．4 B．3 C. D．‎ ‎6.若对任意，函数的值恒大于零，则的 取值范围是（ ）‎ A． B．或 C. 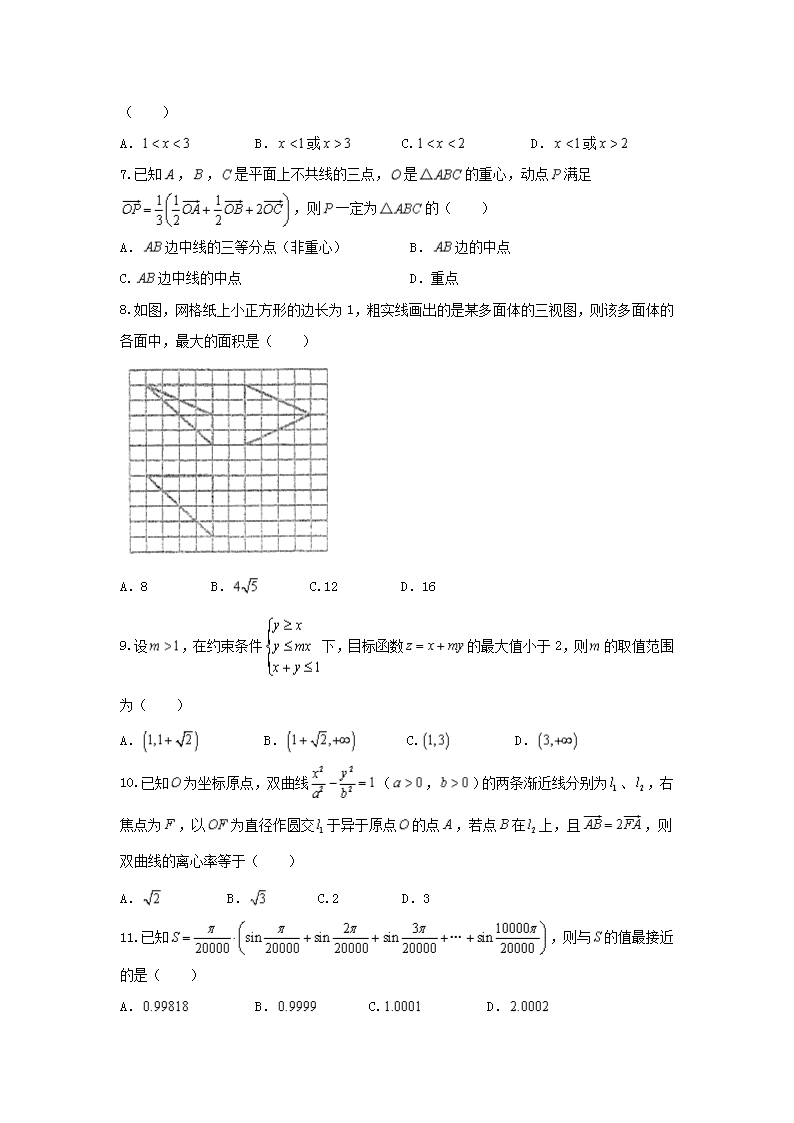D．或 ‎7.已知，，是平面上不共线的三点，是的重心，动点满足，则一定为的（ ）‎ A．边中线的三等分点（非重心） B．边的中点 ‎ C.边中线的中点 D．重点 ‎8.如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各面中，最大的面积是（ ）‎ A．8 B． C.12 D．16‎ ‎9.设，在约束条件下，目标函数的最大值小于2，则的取值范围为（ ）‎ A． B． C. D．‎ ‎10.已知为坐标原点，双曲线（，）的两条渐近线分别为、，右焦点为，以为直径作圆交于异于原点的点，若点在上，且，则双曲线的离心率等于（ ）‎ A． B． C.2 D．3‎ ‎11.已知，则与的值最接近的是（ ）‎ A． B． C. D．‎ ‎12.已知函数（，为自然对数的底数）与的图象上存在关于轴对称的点，则实数的取值范围是（ ）‎ A． B． C. D．‎ 第Ⅱ卷 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.抛物线的准线方程是，则的值为 ．‎ ‎14.平面四边形中，，，，将其沿对角线折成四面体，使平面平面，若四面体的顶点在同一个球面上，则该球的体积为 ．‎ ‎15.已知的三个内角的对边依次为，外接圆的半径为1，且满足，则面积的最大值为 ．‎ ‎16.已知函数，方程有四个实数根，则的取值范围 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. （本小题满分12分）‎ 已知分别是三内角所对的边，.‎ ‎（Ⅰ）求角的大小；‎ ‎（Ⅱ）若等差数列中，，，设数列的前项和为，求证：.‎ ‎18. （本小题满分12分）‎ 如图，在四棱锥中，底面为菱形，，为的中点.‎ ‎（Ⅰ）若，求证：平面平面；‎ ‎（Ⅱ）若平面平面，且，点在线段上，试确定点的位置，使二面角大小为，并求出的值.‎ ‎19. （本小题满分12分）‎ 已知从“神十”飞船带回的某种植物种子每粒成功发芽的概率都为，某植物研究所进行该种子的发芽实验，每次实验种一粒种子，每次实验结果相互独立，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的.若该研究所共进行四次实验，设表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.‎ ‎（Ⅰ）求随机变量的分布列及的数学期望；‎ ‎（Ⅱ）记“不等式的解集是实数集”为事件，求事件发生的概率.‎ ‎20. （本小题满分12分）‎ 已知椭圆，圆的圆心在椭圆上，点到椭圆的右焦点的距离为.‎ ‎（1）求椭圆的方程；‎ ‎（2）过点作互相垂直的两条直线，且交椭圆于两点，直线交圆于，两点，且为的中点，求的面积的取值范围.‎ ‎21. （本小题满分12分）‎ 已知函数，，其中为实数.‎ ‎（Ⅰ）求函数的极值；‎ ‎（Ⅱ）设，若对任意的、（），恒 成立，求实数的最小值.‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22. （本小题满分10分）选修4-4：坐标系与参数方程 已知曲线的极坐标方程为；‎ 曲线的参数方程为（为参数）；将曲线上的所有点的横坐标变为原来的3倍，纵坐标变为原来的倍，得到曲线.‎ ‎（Ⅰ）写出曲线的参数方程和曲线的普通方程；‎ ‎（Ⅱ）已知点，曲线与曲线相交于，两点，求.‎ ‎23. （本小题满分10分）选修4-5：不等式选讲 已知，且.‎ ‎（Ⅰ）求的最小值；‎ ‎（Ⅱ）若存在，使得不等式成立，求实数的取值范围.‎ 数学（理科）参考答案 一、选择题 ‎1-5:DCADA 6-10:BACAB 11、12：CA 二、填空题 ‎13. 14. 15. 16.‎ 三、解答题 ‎17.解：（1）过点作边上的高交与，‎ 则、均为直角三角形，‎ ‎∵，‎ ‎，‎ ‎∵，所以，所以.‎ ‎18.解：（Ⅰ）∵，为的中点，∴，又∵底面为菱形，，∴，‎ 又，∴平面，又∵平面，∴平面平面.……6分 ‎（Ⅱ）∵平面平面，平面平面，，‎ ‎∴平面∴以为坐标原点，分别以为轴 建立空间直角坐标系如图，‎ 则，，，，设，‎ 所以，平面的一个法向量是，‎ 设平面的一个法向量为，所以，‎ 取，……………………9分 由二面角大小为，可得：‎ ‎，解得，此时.…………………………12分 ‎19.解：（1）四次实验结束时，实验成功的次数可能为0，1，2，3，4，相应地，实验失败的次数可能为4，3，2，1，0，所以的可能取值为4，2，0.‎ ‎，‎ ‎，‎ ‎.‎ 所以的分别列为：‎ ‎0‎ ‎2‎ ‎4‎ 期望.………………6分 ‎（2）的可能取值为0，2，4.‎ 当时，不等式为对恒成立，解集为；‎ 当时，不等式为，解集为；‎ 时，不等式为，解集为，不为，‎ 所以.………………12分 ‎20.解：（1）因为椭圆的右焦点为，，∴，‎ ‎∵在椭圆上，∴，‎ 由得，，所以椭圆的方程为.……4分 ‎（2）由题意可得的斜率不为零，当垂直轴时，的面积为.……5分 当不垂直轴时，设直线的方程为：，‎ 则直线的方程为：，，.‎ 由，消去得，‎ 所以，，‎ 则，‎ 又圆心到的距离得，……8分 又，，所以点到的距离点到的距离，‎ 设为，即，‎ 所以的面积.……10分 令，‎ ‎，，‎ 综上，的面积的取值范围为.…………12分 ‎21.（Ⅰ），令，得，列表如下：‎ ‎1‎ ‎+‎ ‎0‎ ‎↗‎ 极大值 ‎↘‎ ‎∴当时，取得极大值，无极小值；……4分 ‎（Ⅱ）当时，时，，，‎ ‎∵在恒成立，∴在上为增函数，‎ 设，∵在上恒成立，‎ ‎∴在上为增函数，‎ 不妨设，则等价于：‎ ‎，即，……6分 设，则在上为减函数，‎ ‎∴在上恒成立，‎ ‎∴恒成立，∴，，……8分 设，∵，‎ ‎∴，∴，为减函数，‎ ‎∴在上的最大值，∴，‎ ‎∴的最小值为.……12分 ‎22.解：（1）的参数方程为（为参数）‎ 的普通方程为.……………………5分 ‎（2）的标准参数方程为（为参数），与联立有，‎ 令，，由韦达定理，‎ 则有.………………10分 ‎23.解：（1）由可知，又因为，‎ 由可知，当且仅当时取等，所以的最小值为8.……5分 ‎（2）由题意可知即解不等式，‎ ‎①，∴.‎ ‎②，∴，‎ ‎③，∴.‎ 综上，.………………10分