- 233.50 KB
- 2023-10-19 发布
22.4 第2课时 平面直角坐标系中的位似
知|识|目|标
通过在平面直角坐标系下进行位似变换,观察图形坐标的变化特点,会在坐标系中利用位似变换把一个图形放大或缩小.
目标 会在平面直角坐标系中作位似图形,并能找出点的坐标变换规律
例 [教材补充例题]如图22-4-4,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以点O为位似中心在y轴的左侧将△OBC放大为原来的两倍,画出图形;
(2)分别写出B,C两点的对应点B′,C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出点M的对应点M′的坐标.
图22-4-4
【归纳总结】当位似图形在原点同侧时,其对应顶点的同名坐标的比为k;当位似图形在原点两侧时,其对应顶点的同名坐标的比为-k;当k>1时,图形扩大;当0<k<1时,图形缩小.
知识点一 图形在平面直角坐标系中位似变换后点
的坐标
在平面直角坐标系中,以原点O为位似中心,相似比为k(k>0)作位似变换,如果原图形上点的坐标为(x,y),那么同向位似图形对应点的坐标为________,反向位似图形对应点的坐标为__________.
[点拨] 这里的相似比指的是新图形与原图形的对应边的比.
知识点二 在平面直角坐标系中作位似图形
3
在平面直角坐标系中,作一个图形关于原点O的位似图形,相似比为k(k>0),可以先找到“关键点”,然后同向直接将坐标乘以相似比k(反向直接将坐标乘以-k),描出点的位置后连线即可.
[点拨] 在平面直角坐标系中,把一个图形进行平移、轴对称、旋转和位似变换,其对应点的坐标变化规律:
(1)平移变换是横坐标或纵坐标加上(或减去)平移的单位.
(2)轴对称变换中,以x轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y轴为对称轴,则纵坐标相等,横坐标互为相反数.
(3)位似变换中,当以原点为位似中心时,变换后与变换前的两个图形对应点的同名坐标之比的绝对值等于相似比.
已知:如图22-4-5,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1∶2把△EFO缩小,则点E的对应点E′的坐标为________.
图22-4-5
[解析] ∵点E的对应点是E′,∴点E′的横、纵坐标分别是点E的横、纵坐标同时乘以,可得点E′的坐标为(-2,1).
上面的答案正确吗?若不正确,请给出正确答案.
3
教师详解详析
【目标突破】
例 [解析] 本题是一道在平面直角坐标系内画位似图形的试题,根据相似比为2∶1,可延长BO到点B′,使B′O=2BO,延长CO到点C′,使C′O=2CO,连接B′C′,则△OB′C′即为所作的位似图形.进一步可以求出点B′,C′的坐标.
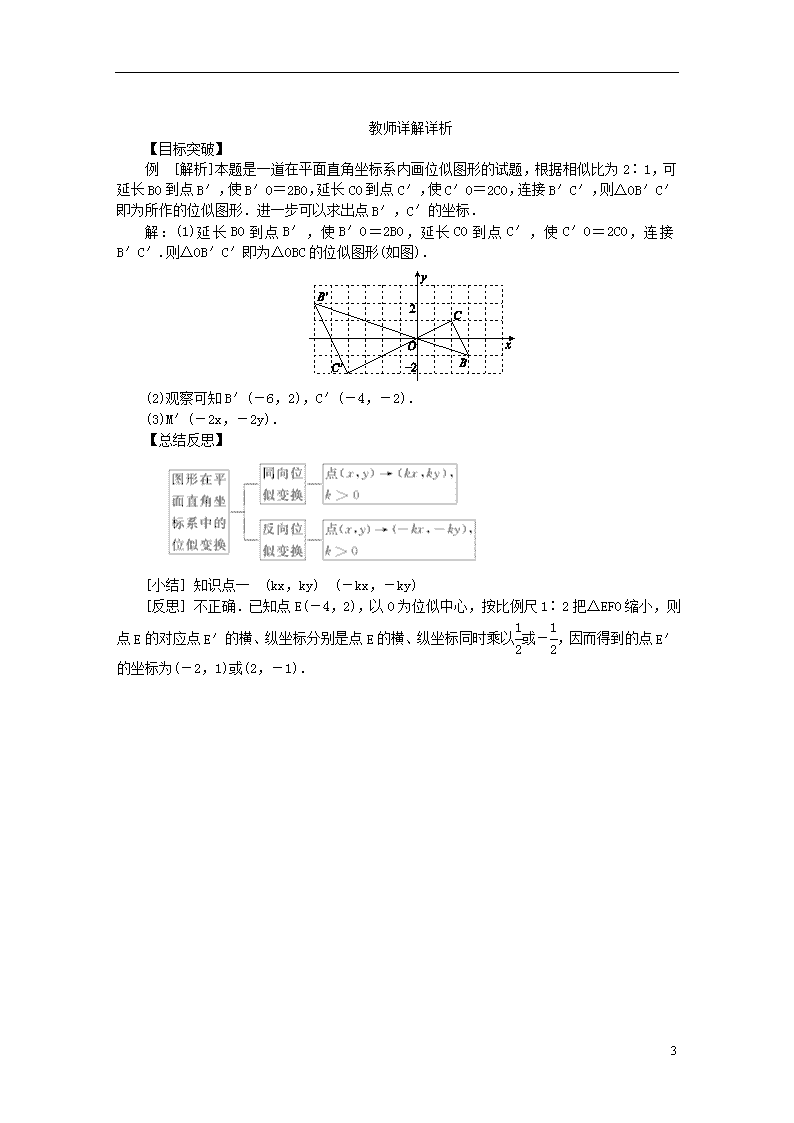
解:(1)延长BO到点B′,使B′O=2BO,延长CO到点C′,使C′O=2CO,连接B′C′.则△OB′C′即为△OBC的位似图形(如图).
(2)观察可知B′(-6,2),C′(-4,-2).
(3)M′(-2x,-2y).
【总结反思】
[小结] 知识点一 (kx,ky) (-kx,-ky)
[反思] 不正确.已知点E(-4,2),以O为位似中心,按比例尺1∶2把△EFO缩小,则点E的对应点E′的横、纵坐标分别是点E的横、纵坐标同时乘以或-,因而得到的点E′的坐标为(-2,1)或(2,-1).
3