2020年环球城市春季赛 O级别奥林匹克竞赛数学试题 2页

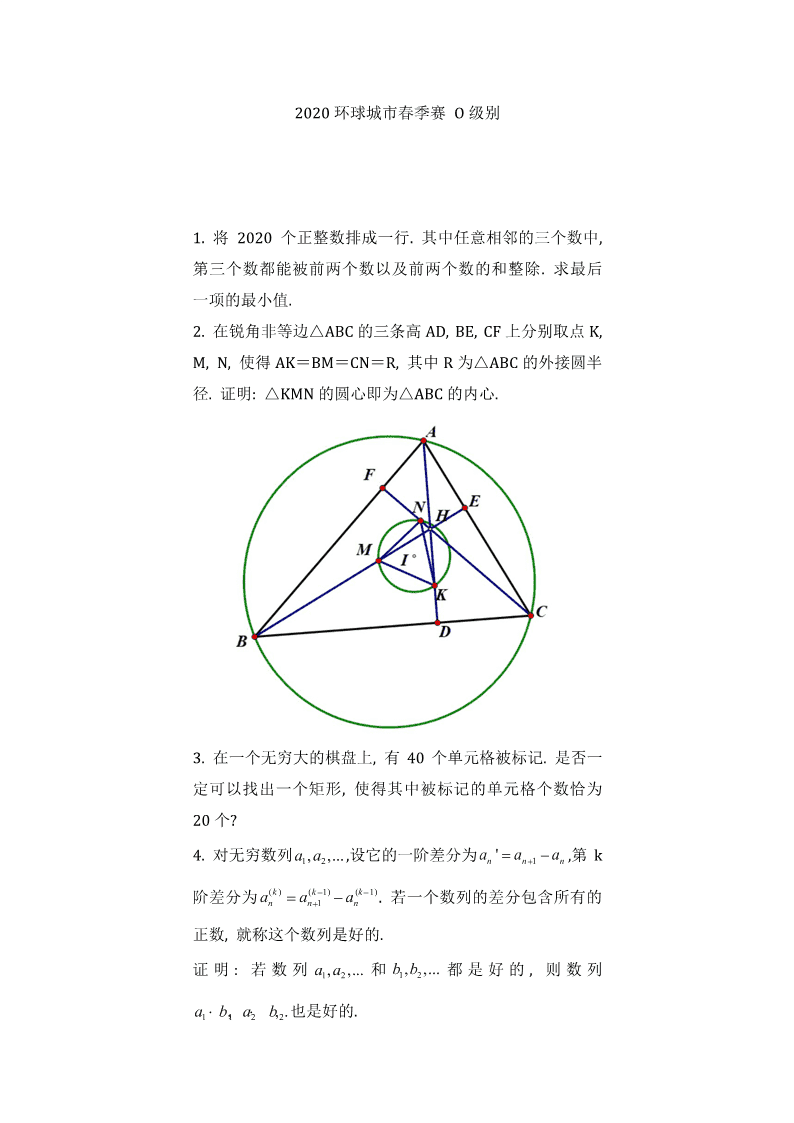
2020 环球城市春季赛 O 级别 1. 将 2020 个正整数排成一行. 其中任意相邻的三个数中, 第三个数都能被前两个数以及前两个数的和整除. 求最后 一项的最小值. 2. 在锐角非等边△ABC 的三条高 AD, BE, CF 上分别取点 K, M, N, 使得 AK＝BM＝CN＝R, 其中 R 为△ABC 的外接圆半 径. 证明: △KMN 的圆心即为△ABC 的内心. 3. 在一个无穷大的棋盘上, 有 40 个单元格被标记. 是否一 定可以找出一个矩形, 使得其中被标记的单元格个数恰为 20 个? 4. 对无穷数列 12, ,...aa ,设它的一阶差分为 1'n n na a a,第 k 阶差分为 ( ) ( 1) ( 1) 1 k k k n n na a a . 若一个数列的差分包含所有的 正数, 就称这个数列是好的. 证明: 若数列 12, ,...aa 和 12, ,...bb 都是好的, 则数列 1 1 2 2, ,...a b a b也是好的. 5. 在半径为 1 的球的球面上取一个球面三角形, 它的三条 边均为球面上半径为 1,长度不超过π的弧,(即这段弧所在的 平面过球心), 其面积正好是球面积的 1 4 . 证明: 将这个球面 三角形复制 4 份,可以覆盖整个球面. 6. 将N个红色, 白色或蓝色的立方体放在圆圈上. 机器人从 圆圈上的某个位置出发, 顺时针移动并执行如下操作, 直到 只剩一个立方体为止: 机器人摧毁自己前方最靠近自己的 两个立方体, 并将一个立方体放置在自己身后,该立方体的 颜色由被摧毁的两个立方体决定: 若这两个立方体颜色相 同, 则被放置的立方体颜色与他们也相同. 若这两个立方体 颜色不同, 则被放置的立方体颜色与他们均不同. 若放置好立方体后, 无论机器人从哪个位置出发, 最终所得 的立方体颜色都不变, 就称这个放置法是好的. 若对整数 N, 所有的放置法都是好的, 就称 N 是成功的. 求所有成功的 N.