- 2.03 MB
- 2023-08-18 发布
滚动小专题(九)与四边形有关的计算与证明
类型1 单种四边形性质与判定的综合运用(解答题)
类型2 多种四边形的综合运用(解答题)
类型1 单种四边形性质与判定的综合运用(解答题)
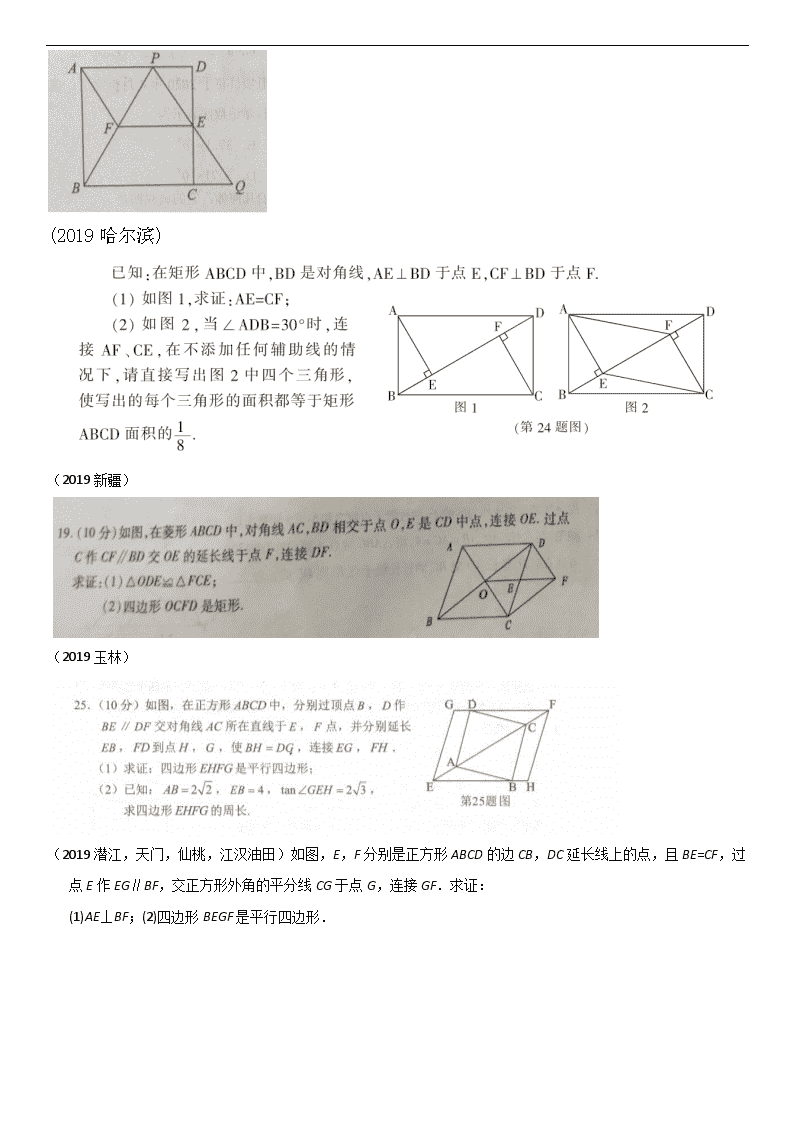
(2019重庆A卷)
(2019贺州)
(2019海南)
(2019哈尔滨)
(2019新疆)
(2019玉林)
(2019潜江,天门,仙桃,江汉油田)如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;(2)四边形BEGF是平行四边形.
(2019鄂州)如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求EF的长.
解:(1)证明:∵ 四边形ABCD是矩形
∴ AB∥CD
∴ ∠DFO=∠BEO,
又因为∠DOF=∠BOE,OD=OB
∴△DOF ≌ △BOE ∴DF=BE
又因为DF∥BE,
∴四边形BEDF是平行四边形.
(2)∵DE=DF,四边形BEDF是平行四边形
∴ BEDF是菱形 ∴ DE=BE,EF⊥BD,OE=OF
设AE=x,则DE=BE=8-x
在Rt△ADE中,根据勾股定理,有AE2+AD2=DE2
∴ x2+62= (8-x)2 解之得:x = 74
∴ DE=8 - 74 = 254
在Rt△ABD中,根据勾股定理,有AB2+AD2=BD2
∴BD=62+82 =10 ∴ OD = 12 BD = 5,
在Rt△DOE中,根据勾股定理,有DE2 - OD2=OE2,
∴ OE = (254)2-52 = 154
∴ EF = 2OE= 15 2
(此题有多种解法,方法正确即可分)
(2019福建)
(2019 枣庄)
(2019重庆A卷)
25.如图,在平行四边形ABCD中,点E在边BC上,连结AE,EM⊥AE,垂足为E,交CD于点M,
AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P显AD上一点,连接CP.
(1)若DP=2AP=4,CP=,CD=5,求△ACD的面积.
(2)若AE=BN,AN=CE,求证:AD=CM+2CE.
(2019 泰安)
(2019 南充)
(2019 安徽)
(2019 凉山州)
(2019 青岛)
21.(本小题满分 8 分)
如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.
答案:
类型2 多种四边形的综合运用(解答题)
22. (2019宿迁)如图,矩形ABCD中,AB=4,BC=2,点E、F分别在AB、CD上,且BE=DF=3/2,
⑴ 求证:四边形AECF是菱形[来源:学科网]
⑵ 求线段EF的长.
(2019 滨州)
(2019 泰安)
(2019 宁波)
答案: