- 135.50 KB
- 2023-07-09 发布
22.1. 2 二次函数y=ax²的图像和性质
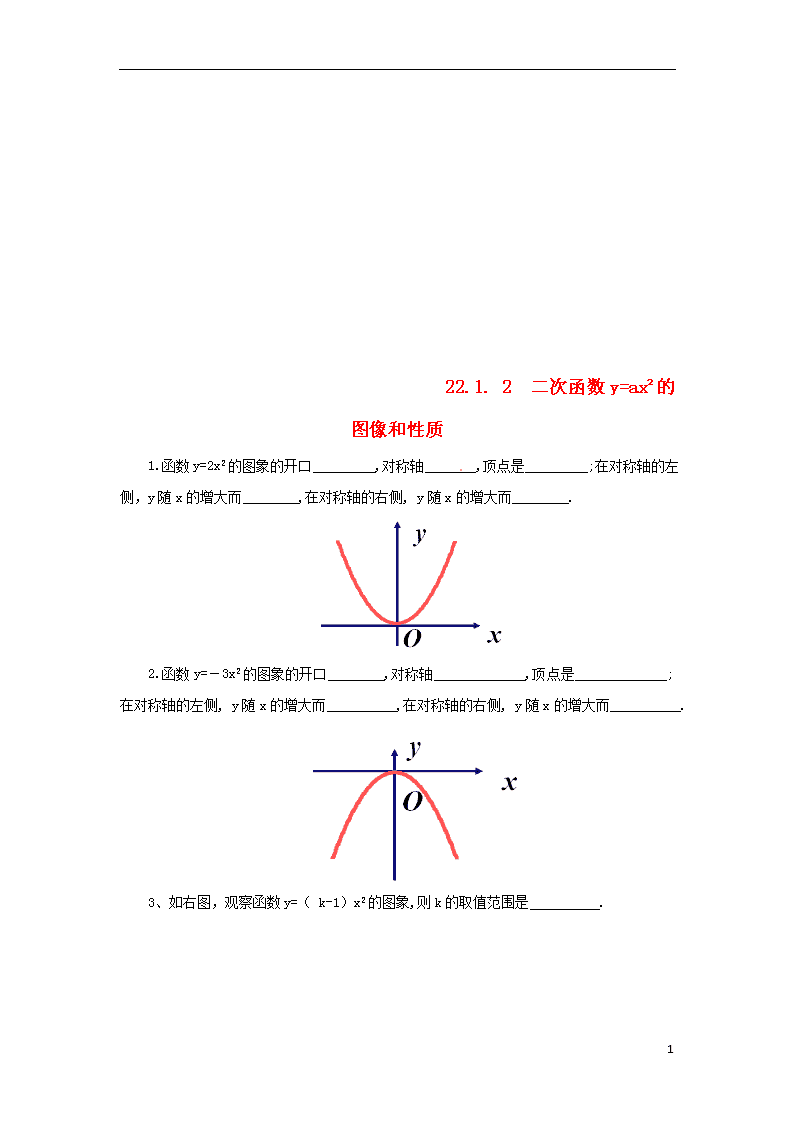
1.函数y=2x2的图象的开口 ,对称轴 ,顶点是 ;在对称轴的左侧,y随x的增大而 ,在对称轴的右侧, y随x的增大而 .
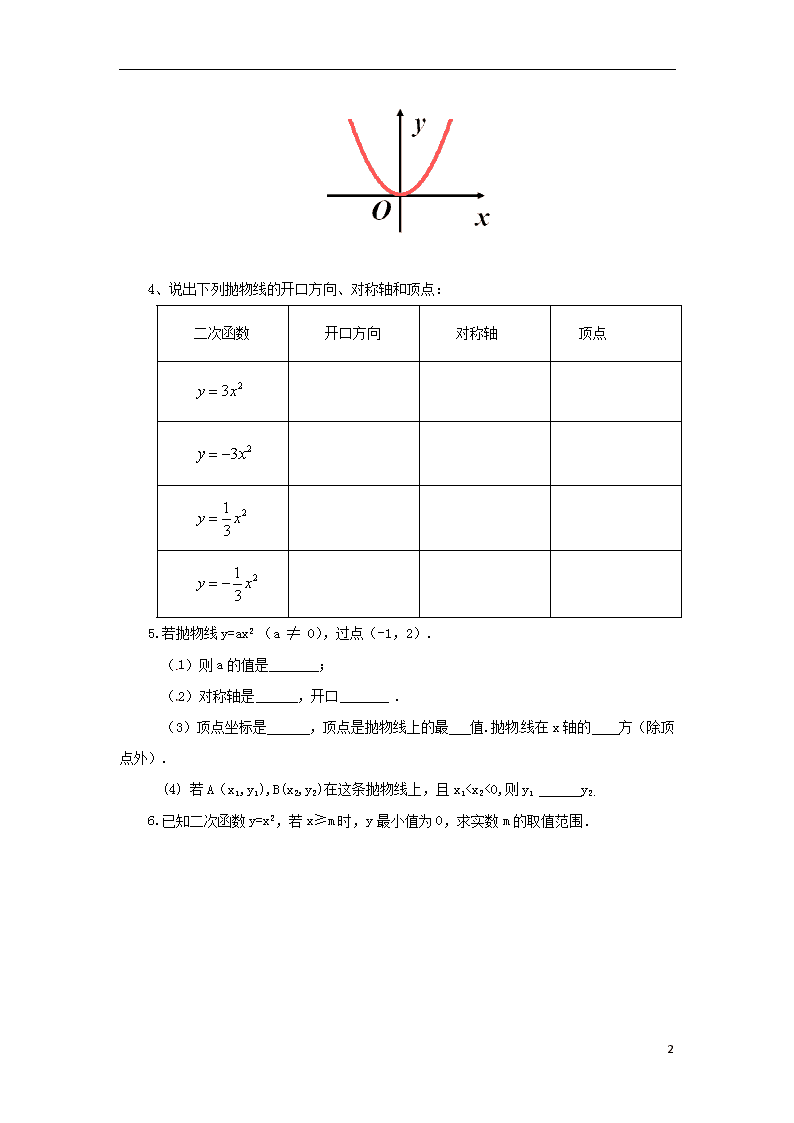
2.函数y=-3x2的图象的开口 ,对称轴 ,顶点是 ;在对称轴的左侧, y随x的增大而 ,在对称轴的右侧, y随x的增大而 .
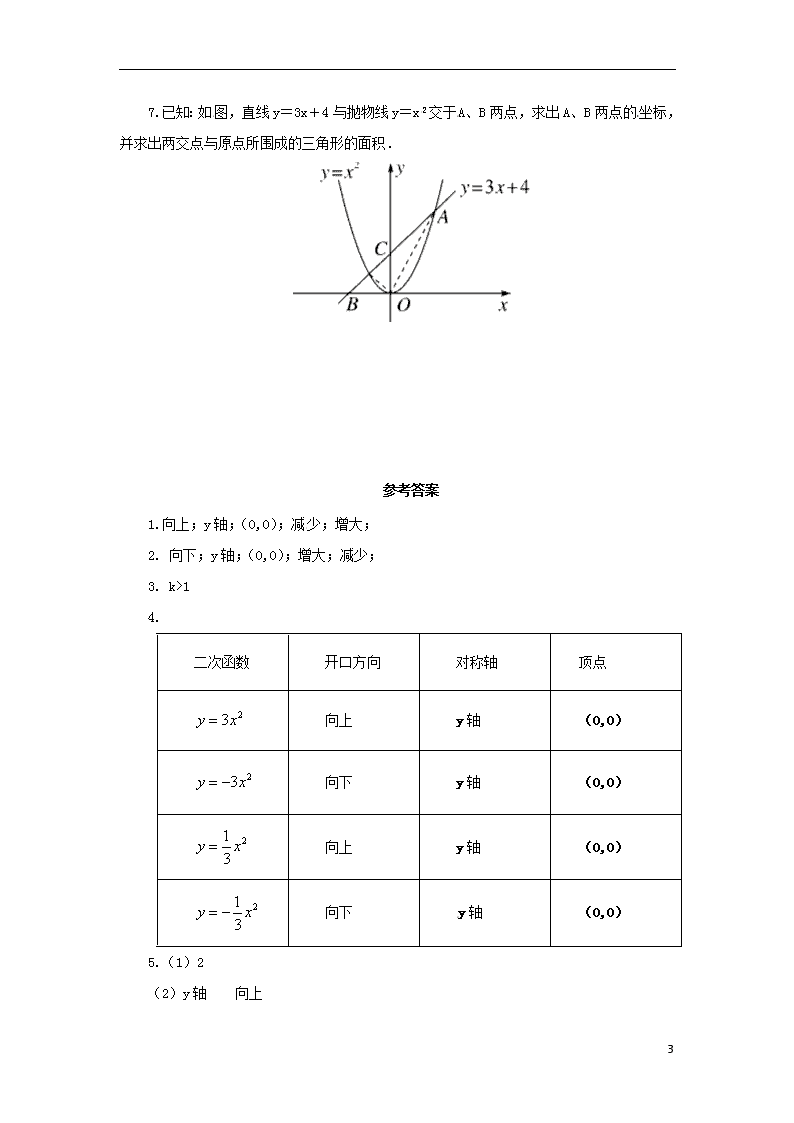
3、如右图,观察函数y=( k-1)x2的图象,则k的取值范围是 .
4
4、说出下列抛物线的开口方向、对称轴和顶点:
二次函数
开口方向
对称轴
顶点
5.若抛物线y=ax2 (a ≠ 0),过点(-1,2).
(1)则a的值是 ;
(2)对称轴是 ,开口 .
(3)顶点坐标是 ,顶点是抛物线上的最 值 .抛物线在x轴的 方(除顶点外).
(4) 若A(x1,y1),B(x2,y2)在这条抛物线上,且x11
4.
二次函数
开口方向
对称轴
顶点
向上
y轴
(0,0)
向下
y轴
(0,0)
向上
y轴
(0,0)
向下
y轴
(0,0)
5.(1)2
(2)y轴 向上
4
(3)(0,0) 小 上
(4)>
6. 解:∵二次函数y=x2,
∴当x=0时,y有最小值,且y最小值=0,
∵当x≥m时,y最小值=0,
∴m≤0.
7. 解:由题意得
解得
所以此两函数的交点坐标为A(4,16)和B(-1,1).
∵直线y=3x+4与y轴相交于点C(0,4),即CO=4.
∴S△ACO=·CO·4=8,S△BOC=×4×1=2,
∴S△ABO=S△ACO+S△BOC=10.
4