- 83.50 KB
- 2023-06-22 发布
同底数幂的乘法
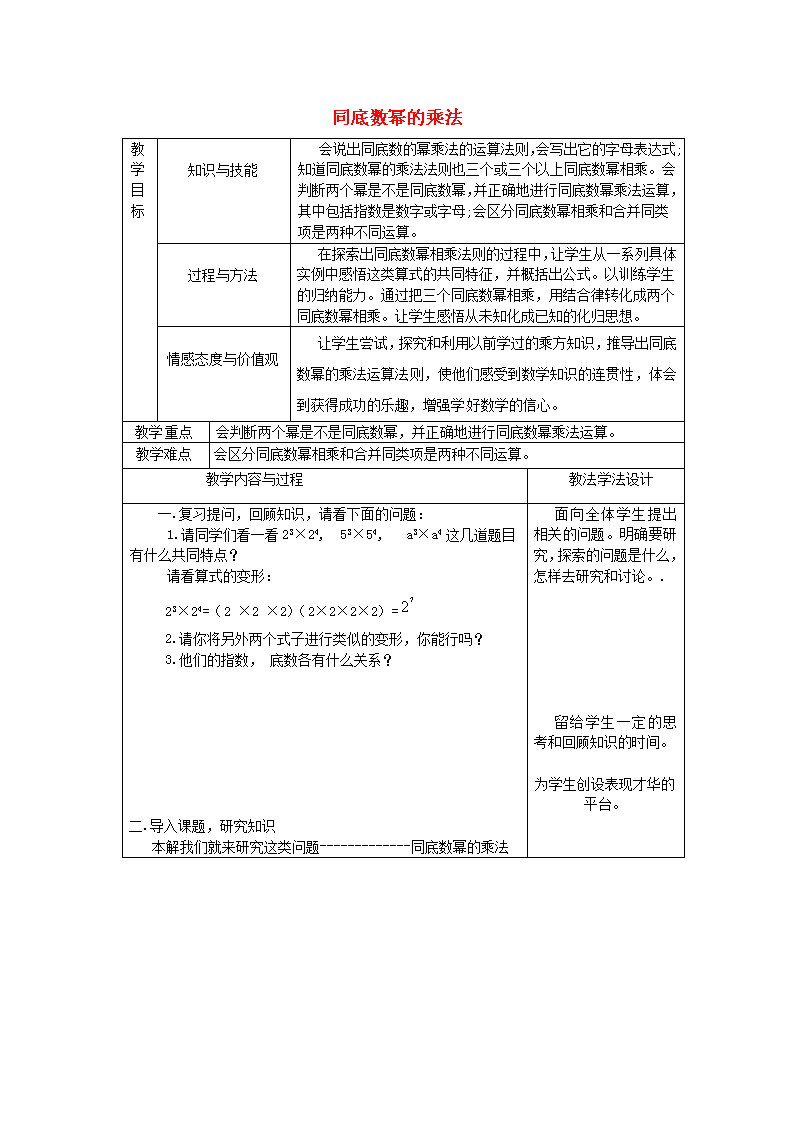
教学目标
知识与技能
会说出同底数的幂乘法的运算法则,会写出它的字母表达式;知道同底数幂的乘法法则也三个或三个以上同底数幂相乘。会判断两个幂是不是同底数幂,并正确地进行同底数幂乘法运算,其中包括指数是数字或字母;会区分同底数幂相乘和合并同类项是两种不同运算。
过程与方法
在探索出同底数幂相乘法则的过程中,让学生从一系列具体实例中感悟这类算式的共同特征,并概括出公式。以训练学生的归纳能力。通过把三个同底数幂相乘,用结合律转化成两个同底数幂相乘。让学生感悟从未知化成已知的化归思想。
情感态度与价值观
让学生尝试,探究和利用以前学过的乘方知识,推导出同底数幂的乘法运算法则,使他们感受到数学知识的连贯性,体会到获得成功的乐趣,增强学好数学的信心。
教学重点
会判断两个幂是不是同底数幂,并正确地进行同底数幂乘法运算。
教学难点
会区分同底数幂相乘和合并同类项是两种不同运算。
教学内容与过程
教法学法设计
一.复习提问,回顾知识,请看下面的问题:
1.请同学们看一看23×24, 53×54, a3×a4这几道题目有什么共同特点?
请看算式的变形:
23×24=(2 ×2 ×2)(2×2×2×2)=
2.请你将另外两个式子进行类似的变形,你能行吗?
3.他们的指数, 底数各有什么关系?
二.导入课题,研究知识
本解我们就来研究这类问题-------------同底数幂的乘法
面向全体学生提出相关的问题。明确要研究,探索的问题是什么,怎样去研究和讨论。.
留给学生一定的思考和回顾知识的时间。
为学生创设表现才华的平台。
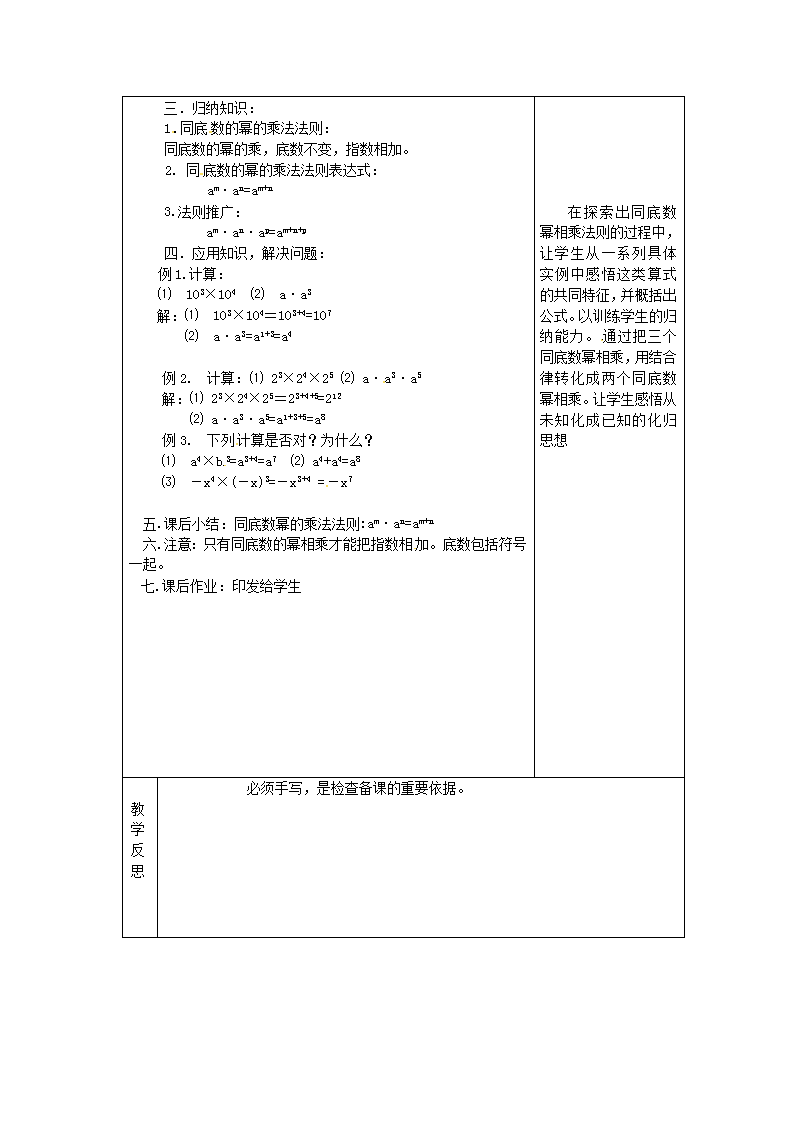
三.归纳知识:
1.同底数的幂的乘法法则:
同底数的幂的乘,底数不变,指数相加。
2. 同底数的幂的乘法法则表达式:
am·an=am+n
3.法则推广:
am·an·ap=am+n+p
四.应用知识,解决问题:
例1.计算:
⑴ 103×104 ⑵ a·a3
解:⑴ 103×104=103+4=107
⑵ a·a3=a1+3=a4
例2. 计算:⑴ 23×24×25 ⑵ a·a3·a5
解:⑴ 23×24×25=23+4+5=212
⑵ a·a3·a5=a1+3+5=a8
例3. 下列计算是否对?为什么?
⑴ a4×b3=a3+4=a7 ⑵ a4+a4=a8
⑶ -x4×(-x)3=-x3+4 =-x7
五.课后小结:同底数幂的乘法法则:am·an=am+n
六.注意:只有同底数的幂相乘才能把指数相加。底数包括符号一起。
七.课后作业:印发给学生
在探索出同底数幂相乘法则的过程中,让学生从一系列具体实例中感悟这类算式的共同特征,并概括出公式。以训练学生的归纳能力。通过把三个同底数幂相乘,用结合律转化成两个同底数幂相乘。让学生感悟从未知化成已知的化归思想
教学反思
必须手写,是检查备课的重要依据。