- 475.00 KB
- 2023-06-10 发布
第一部分 夯实基础 提分多
第一单元 数与式
第
5
课时
分 式
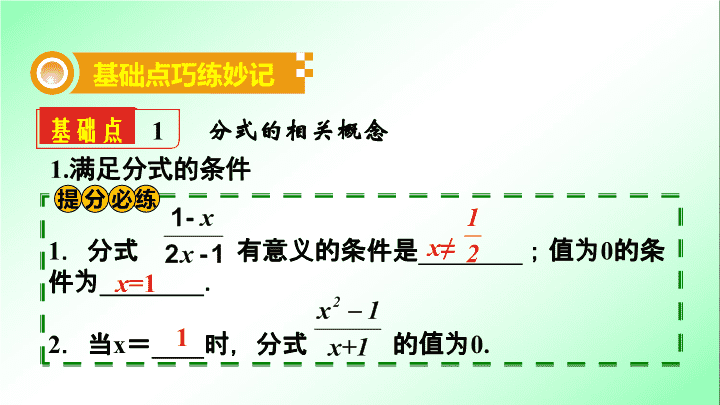
基础点
1
分式的相关概念
基础点巧练妙记
1
.分式
有意义的条件是
________
;值为
0
的条件为
________
.
2
.当
x
=
____
时,分式
的值为
0.
练
提
分
必
x
≠
x
=1
1
1.
满足分式的条件
2.
最简分式:分子分母没有公因式的分式.
【温馨提示】
①
使分式
有意义的条件是分母
g≠0
,无
意义的条件是分母
g
=
0
;
②
分式
的值为
0
的条件是分子
f
=
0
且分母
g≠0.
基础点
2
分式的
基本性质
1.
性质
:分式的分子与分母同乘以
(
或除以
)
同一个不为零的整式,分式值不变,即
,其中
a
、
b
、
c
是整式,
c
≠
0.
2.
约分的关键是确定公因式,其方法为
:
(1)
取分子、分母系数的最大公约数作为公因式的系数;
(2)
取各个公因式的最低次幂作为公因式的因式;
(3)
如果分子、分母是多项式,则应先把分子、分母分解因式,然后判断公因式.
3.
通分的关键是确定最简公分母,其方法为:
(1)
取各个分母系数的最小公倍数作为最简公分母的系数;
(2)
取各个公因式的最高次幂作为最简公分母的因式;
(3)
如果分母是多项式,则应先把每个分母分解因式然后判断最简公分母.
基础点
3
分式
运算
1.
加减运算
同分母分式相加减,分母不变,分子相加减:
=
①
________
;
异分母分式相加减,先通分,变为同分母的分式再加减:
=
②
________±
=
.
2.
乘除运算
步骤:
①
除变乘
(
乘倒数
)
;
②
分解因式
(
将各分式的分子分母分解因式
)
;
③
约分
(
约去公因式
)
;④约分后分子分母分别相乘.
3.
分式化简求值的注意事项
(1)
分式化简与分式方程混淆,通分后去掉分母;
(2)
丢掉符号:分式化简中最关键的步骤是通分,不仅要考虑最简公分母,也要注意符号的变化.常见的符号变形有:
x
-
y
=-
(
y
-
x)
,-
x
-
y
=-
(
x
+
y
)
等;
(3)
求值时,代值错误:当所给值不唯一时,一定要注意选值时应该使原分式和化简过程中的分式都有意义,即保证分母不为
0.
3
.计算:
(1)
=
____________
;
(2)
=
____________
;
练
提
分
必
1
(3)
=
___________
;
(4)
=
____________
;
(5)
=
_______
.
练
提
分
必
-1
分式化简与解分式方程相混淆
化简
:
小刚:
解:
原式=
2(
a
+
2)
-
8
=
2
a
+
4
-
8
=
2
a
-
4.
2
失
分
点
小芳:
解:
原式
上述小刚与小芳的解题过程谁的不正确?请分析错因
2
失
分
点
解:
小刚的解题过程不正确,因为进行加减法运算时,如果是异分母,应先通分再计算,而不是直接去掉分母
2
失
分
点
类型
分式的化简求值
重难点精讲优练
一、整体通分法
例1
计算:
.
二
、先约分后通分法
例
2
计算:
.
解:
原式
练习
1
计算
:
.
练习
2
先化简再求值
:
,其中
x=-2.
练习
3
先化简再求值
:
,其中
解:
原式
原式
练习
3
先化简: ,
然后在不
等式
x≤2
的非负整数解中选择一个适当的数代入求值.
解:
原式
把
x
=
0
代入得:
或把
x
=
2
代入得:
(
二选一即可
)