- 3.36 MB
- 2023-05-11 发布
书书书
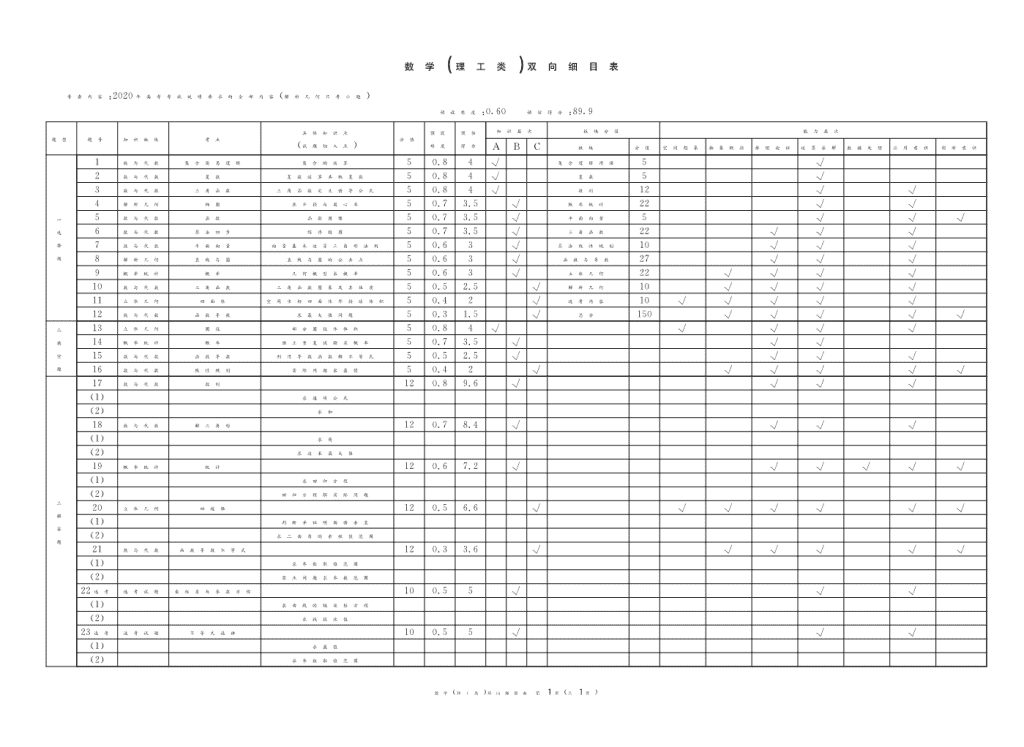
数学!理工类"双向细目表 第 !!!!! 页!共!页"
数学!理工类"双向细目表
!!考查内容!!"!"年高考考试说明要求的全部内容"解析几何只考小题#
预设难度!"#$"!!预估得分!%&#&
题型 题号 知识板块 考点 具体知识点
"试题切入点# 分值 预设
难度
预估
得分
知识层次 板块分值 能力层次
' ( ) 板块 分值 空间想象 抽象概括 推理论证 运算求解 数据处理 应用意识 创新意识
一
选
择
题
* 数与代数 集合简易逻辑 集合的运算 + ",% - " 集合逻辑用语 + "
! 数与代数 复数 复数运算共轭复数 + ",% - " 复数 + "
. 数与代数 三角函数 三角函数定义诱导公式 + ",% - " 数列 *! " "
- 解析几何 椭圆 焦半径与离心率 + ",/ .,+ " 概率统计 !! " "
+ 数与代数 函数 函数图像 + ",/ .,+ " 平面向量 + " " "
$ 数与代数 算法初步 程序框图 + ",/ .,+ " 三角函数 !! " " "
/ 数与代数 平面向量 向量基本运算三角形法则 + ",$ . " 算法线性规划 *" " " "
% 解析几何 直线与圆 直线与圆的公共点 + ",$ . " 函数与导数 !/ " " "
& 概率统计 概率 几何概型求概率 + ",$ . " 立体几何 !! " " " "
*" 数与代数 三角函数 三角函数图象及其性质 + ",+ !,+ " 解析几何 *" " " " "
** 立体几何 四面体 空间坐标四面体外接球体积 + ",- ! " 选考内容 *" " " " " "
*! 数与代数 函数导数 求最大值问题 + ",. *,+ " 总分 *+" " " " " "
二
填
空
题
*. 立体几何 圆柱 部分圆柱体体积 + ",% - " " " " "
*- 概率统计 概率 独立重复试验求概率 + ",/ .,+ " " "
*+ 数与代数 函数导数 利用导数函数解不等式 + ",+ !,+ " " " "
*$ 数与代数 线性规划 实际问题求最值 + ",- ! " " " " " "
三
解
答
题
*/ 数与代数 数列 *! ",% &,$ " " " "
"*# 求通项公式
"!# 求和
*% 数与代数 解三角形 *! ",/ %,- " " " "
"*# 求角
"!# 求边长最大值
*& 概率统计 统计 *! ",$ /,! " " " " " "
"*# 求回归方程
"!# 回归方程解实际问题
!" 立体几何 四棱锥 *! ",+ $,$ " " " " " " "
"*# 判断并证明面面垂直
"!# 求二面角的余弦值范围
!* 数与代数 函数导数不等式 *! ",. .,$ " " " " " "
"*# 求参数取值范围
"!# 零点问题求参数范围
!!选考 选考试题 坐标系与参数方程 *" ",+ + " " "
"*# 求曲线的极坐标方程
"!# 求线段比值
!.选考 选考试题 不等式选讲 *" ",+ + " " "
"*# 求最值
"!# 求参数取值范围
书书书
数学!理工类"试题答案 第 !!!!! 页!共"页"
高!"#$级第一次诊断性考试
数学!理工类"参考答案
评分说明!
!"本解答给出了一种或几种解法供参考!如果考生的解法与本解答不同!可根据试题的主要
考查内容比照评分参考制定相应的评分细则"
#"对计算题!当考生的解答在某一步出现错误时!如果后继部分的解答未改变该题的内容和
难度!可视影响的程度决定后继部分的给分!但不得超过该部分正确解答应得分数的一半#如果
后继部分的解答有较严重的错误!就不再给分"
$"解答右端所注分数!表示考生正确做到这一步应得的累加分数"
%"只给整数分"选择题和填空题不给中间分"
一"选择题#&'分$
!!命题意图#本小题考查集合运算$不等式解法$指数式的值等基础知识%考查运算求解能力!
解析#选择 ($因为") #"##*$#*!'#& '' ) #"*####& '+ $$)&!$#$%$,$('$所以 "$$)
&!$#$%'!
#!命题意图#本小题考查复数的运算$共轭复数概念等基础知识%考查运算求解能力!
解析#选择 -$由%)!!./"!#./")!.$/$所以其共轭复数%%)!*$/!
$!命题意图#本小题考查三角函数的定义)诱导公式等基础知识%考查运算求解能力$应用意识!
解析#选择 0$角!的终边经过点& *槡$
#$*! "!
#
$所以123!)*槡$
#$所以123!!.!")*123!)槡$
#!
%!命题意图#本小题考查椭圆的定义$基本量的关系$离心率等基础知识%考查运算求解能力$数
形结合思想$应用意识!
解析#选择 -$由题意有' 槡) $($所以) 槡) #($所以离心率*))
' )槡#(
槡$(
)槡&
$ !
+!命题意图#本小题考查函数图象和性质等知识%考查数形结合等数学思想!
解析#选择 -$由题当#&*4时$+!#"&.4$排除 0$(%当#&.4时$+!#"&'!
&!命题意图#本小题考查程序框图及其应用$指数式和对数式求值等基础知识%考查运算求解能
力$应用意识!
解析#选择($依程序框图运行$当输入#)*#时$输出')#*#)!
%$当输入#)!
5时$输出,)
()627$
!
5)*#$则'.()!
%*#)*8
%!
8!命题意图#本小题考查平面向量的基本运算$三角形法则等基础知识%考查数形结合思想$运算
求解能力$应用意识!
数学!理工类"试题答案 第 #!!!! 页!共"页"
解析#选择 ($因为 &''-.) &''-". &''".)!
#
&''$".!
$
&''"/)!
#
&''$".!
$!&''$/* &''$"")!
&
&''$".!
$
&''$/)
*!
&
&''"$.!
$
&''$/$所以")*!
&$#)!
$!故".#)!
&!
,!命题意图#本小题考查直线和圆的方程$点到直线的距离$直线与圆的位置关系等基础知识%考
查运算求解能力$分类讨论思想$数形结合思想$应用意识!
解析#选择 ($圆的标准方程为!#.!"#.!,*!"#)%$圆心!*!$!"到直线0##., 槡. #)'的
距离为1)" 槡*!.!. #"
!#.!槡 # )!(#!圆的半径"$结合图形知$圆上有三点到直线0的距离为!!
5!命题意图#本小题考查概率等基本知识$渗透数学文化$考查抽象概括能力和应用意识!
解析#选择 ($设图"三角形的面积为2$则图#中每个小阴影三角形的面积为图"三角形面
积的2
&%$于是所求的概率为 &)
#8
&%2
2 )#8
&%!
!'!命题意图#本小题考查三角函数图象及其性质等基础知识%考查逻辑推理能力$数形结合思
想$应用意识!
解析#选择 9$由+!#!")+!##")!知!#!$!"$!##$!"是+!#")$3/: ##*!! "$ .!图象的两
个对称中心$则#!*## 是3
#)!
#的整数倍!3 是函数+!#"的最小正周期"$结论"错误%因为
+ #!! "$ )$3/:!.!)!$所以结论$正确%由#4!*!
####*!
$##4!.!
#!4)%"解得4!* !
!#
###4!.+!
!#!4)%"$当4)'时$+!#"在 *!
!#$+!* +!# 上单调递增$则+!#"在 '$+!* +!# 上单调递
增$在 +!
!#$!* +# 上单调递减$结论%错误%,)+!#"的图象向右平移 !
!#个单位长度后所得图象
对应的函数为,)$3/: # #*!! "!# *!! "$ .!)*$123##.!$是偶函数$所以图象关于, 轴对
称$结论#正确!
!!!命题意图#本小题考查空间直角坐标系$空间几何体的外接球$球的体积等基础知识%考查空
间想象能力$推理论证能力$运算求解能力$应用意识!
解析#选择 -$由题意知$该四面体侧棱 &"*底面 "$/$且底面是边长为 槡# $的正三角形$侧
棱 &")#$所以底面正三角形的外接圆半径为#$球心必在过 &" 中点且平行于底面的平面
上$所以球半径5) ##.!槡 # 槡) +$所以球的体积为%
$!!槡+"$) 槡#' +
$ !!
!#!命题意图#本小题考查导数的几何意义)函数与导数综合运用等知识%考查抽象概括等数学能
力以及数学抽象能力$考查函数与方程)化归与转化等数学思想!
解析#选择 ($设切点!#'$6:!'#'.(""$则由+6!#'") '
'#'.()#得'#'.()!
#'!'+'"$又
由6:!'#'.(")##'$得#')!
#6:!'#'.(")!
#6:'
#$则()'
#*'#')'
#*'
#6:'
#$有'()
数学!理工类"试题答案 第 $!!!! 页!共"页"
!
#'#*!
#'#6:'
#!'+'"$令7!'")!
#'#*!
#'#6:'
#$则76!'")' !
#*6:'! "# $故当'('( 槡#;
时76!'"+'%当'+ 槡#;时76!'"('$故当' 槡)#;时7!'"取得极大值也即最大值7!槡#;");!
二"填空题##'分$
!$!命题意图#本小题考查圆柱的体积公式$扇形的面积等基础知识%考查空间想象能力$运算求
解能力$应用意识!
解析#填!'! 槡.$ $$由题意知圆柱截掉后剩余部分的底面面积为!'!
$ 槡. $$所以剩余部分的
体积为!'! 槡.$ $!
!%!命题意图#本小题考查概率)独立重复试验等基础知识$考查抽象概括能力和应用意识!
解析#填#'
#8$甲获胜的方式有#<'和#+$%"$!,$%"$!,$'"$!8>+$'"围 成 的 梯 形 及 其 内 部$包 含 的 整 点 有 !,$'"$!8$!"$
!,$!"$!+$#"$!&$#"$!8$#"$!,$#"$!%$$"$!+$$"$!&$$"$!8$$"$!,$$"$!$$%"$!%$%"$!+$%"$
!&$%"$!8$%"$!,$%"!作直线$#'#.+'%,)'并平移$分析可得当直线过点!,$'"时%最小$即
%?/:),=$#')#+&'!元"!
三"解答题#共8'分$
!8!命题意图#本小题考查等差数列)等比数列的通项公式$前9 项和公式及其应用等基础知识%
考查运算求解能力$应用意识!
解析#!!"由题意有#'9)29.%$
当9)!时$#'!)'!.%$所以'!)%! #分………………………………………………………
当9,#时$29)#'9*%$29*!)#'9*!*%$
数学!理工类"试题答案 第 %!!!! 页!共"页"
两式相减得'9)29*29*!)#'9*#'9*!$整理得 '9
'9*!
)#$
所以数列&'9'是以%为首项$#为公比的等比数列! &分………………………………………
所以数列&'9'的通项公式'9)%=#9*!)#9.!!9)'- "! 8分…………………………………
!#"由#(9 )'#
9)##9.#$
所以(9)#9.#$
所以数列&(9'是以%为首项$#为公差的等差数列! !'分………………………………………
所以 39)%9.9!9*!"
# =#)9#.$9! !#分……………………………………………………
!,!命题意图#本小题考查正弦定理$两角和的正弦公式$三角函数求最值等基础知识%考查运算
求解能力$逻辑推理能力$应用意识!
解析#!!"由'123/.!
#))($根据正弦定理有#
3/:"123/.!
#3/:/)3/:$! #分…………………………………………………………………
所以3/:"123/.!
#3/:/)3/:!"./")3/:"123/.123"3/:/$
所以!
#3/:/)123"3/:/! %分……………………………………………………………………
因为/ 为三角形内角$所以3/:/1'$
所以123")!
#$
因为 " 为三角形内角$所以 ")!
$! &分…………………………………………………………
!#"由' 槡) $$")!
$$根据正弦定理有#
(
3/:$) )
3/:/) '
3/:")#$
所以()#3/:$$))#3/:/! ,分……………………………………………………………………
所以(.))#3/:$.#3/:/)#3/: #!
$ *! "/ .#3/:/
槡) $123/.$3/:/
槡)# $3/: /.!! "& # 槡# $! !!分…………………………………………………………………
当/)!
$时$等号成立!
所以(.)的最大值为 槡# $! !#分…………………………………………………………………
另解#!#"由' 槡) $$")!
$$根据余弦定理有#
!槡$"#)(#.)#*#()123!
$$
数学!理工类"试题答案 第 &!!!! 页!共"页"
即$)(#.)#*()! ,分……………………………………………………………………………
因为(#.)#*())!(.)"#*$(),!(.)"#*$(.)! "#
#
)!(.)"#
% $
所以$,!(.)"#
% ! !!分……………………………………………………………………………
即(.)# 槡# $$当且仅当()) 槡) $时$等号成立!
所以(.)的最大值为 槡# $! !#分…………………………………………………………………
!5!命题意图#本小题考查回归方程)统计案例等基本知识$考查回归分析的基本思想$考查抽象
概括等能力和应用意识$以及数据分析能力!
解析#!!"由题$%与温度# 又可以用线性回归方程来拟合$设:%):'.:(#!
:(;
2
8
<;!
!#< =3#"!%< =%%"
2
8
<;!
!#< =3#"#
;%&>%!,
!,# 4'>#++$ %分……………………………………………
所以:' ;%%=:(3# ;$>+$8='>#++>#8;=$>$%,$
故%关于# 的线性回归方程为:%)'>#++#*$>$%,> ,分………………………………………
!#"由!!"可得6:,)'>#++#*$>$%,$
于是产卵数, 关于温度# 的回归方程为,);'>#++#*$>$%,!
当#)#&时$,);'>#++=#&*$>$%,);$>#,#4#8%
当#)$&时$,);'>#++=$&*$>$%,);+>,$#4$%!%
因为函数,);'>#++#*$>$%,单调递增$
所以$在气温在#&@&$&@之间时$一只该品种昆虫的产卵数的估计范围是*#8$$%!+的正整
数! !#分……………………………………………………………………………………………
#'!命题意图#本小题考查四棱锥$平面与平面垂直的判定定理$二面角的余弦值等基础知识%考
查空间想象能力$推理论证能力$运算求解能力$创新意识!
解析#!!"因为 &")"$$. 为线段&$ 的中点!
所以 ".*&$! #分………………………………………………………………………………
因为 &"*底面 "$/-$$/5平面 "$/-$
所以$/*&"$
又因为底面 "$/- 为正方形$所以$/*"$$
&"$"$)"$
所以$/*平面 &"$$
因为 ".5平面 &"$$
所以 ".*$/! %分………………………………………………………………………………
因为 &$$$/)$$
所以 ".*平面 &$/$
因为 ".5平面 ".?$
所以平面 ".?*平面 &$/! &分…………………………………………………………………
数学!理工类"试题答案 第 '!!!! 页!共"页"
!#"由题意$以 "$$"- 所在直线分别为#$, 轴建立空间直角坐标系如图所示$令 &")#$
则 "!'$'$'"$$!#$'$'"$.!!$'$!"$?!#$@$'"!其中'(@##"!
易知平面$"? 的一个法向量!)!'$'$!"! ,分…………………
设平面 ".? 的法向量")!#$,$%"$
由
", &''"?)'$
", &''".)'
.
/
0 !
即 ##.@,)'$
#.%)'.
/
0 !
令%)!$则") *!$#
@$! "! 是平面 ".? 的一个法向量! !'分…………………………………
123-!$".) !,"
"!",""") !
!*!"#. #! "@
#
.!槡 #
) !
#.%
@槡 #
$
由'(@##$所以 #.%
@槡 # ) 槡$$.4* "$
所以 !
#.%
@槡 #
) '$槡$! +$ !
故若? 为线段$/ 上的动点!不含$"$二面角$*"?*. 的余弦值的取值范围是 '$槡$! +$ !
!#分……………………………………………………………………………………………
#!!命题意图#本小题考查函数图象和性质)函数零点)导数在研究函数中的应用等基本知识$考
查了学生化归与转化)推理论证等数学思想$以及数学抽象)数学运算等能力!
解析#!!"由+!#")#;#*'6:#*'#.'*;!#+'"$得
+6!#");#!!.#"*'!!.#"
# )!!.#"!#;#*'"
# $
因为+!#"为单调函数$
所以当#+'时+6!#",'或+6!#"#'恒成立$
由于#.!+!$于是只需'##;# 或',#;# 对于#+'恒成立$ #分…………………………
令A!#")#;#$则A6!#")!#.!";#$
当#+'时$A6!#"+'$所以A!#")#;# 为增函数$
则A!#"+A!'")'!又当#&.4时$A!#"&.4$
则',#;# 不可能恒成立$即+!#"不可能为单调减函数!
当'#A!'"$即'#'时$'##;# 恒成立$
此时函数为单调递增函数! %分…………………………………………………………………
!#"因为+!!")'$所以#)!是+!#"的一个零点!
由!!"知$当'#'时$+!#"为!'$.4"的增函数$
此时关于# 的方程+!#")'仅一解#)!$即函数+!#"仅一个零点$满足条件! &分………
当'+'时$由+6!!")'得');$
!'"当');时$+!#")#;#*;6:#*;#$
数学!理工类"试题答案 第 (!!!! 页!共"页"
则+6!#")!!.#"!#;#*;"
# $
令B!#")#;#*;$
易知B!#"为!'$.4"的增函数$且B!!")'$
所以当'(#(!时$B!#"('$即+6!#"('$+!#"为减函数$
当#+!时$B!#"+'$即+6!#"+'$+!#"为增函数$
所以+!#",'在!'$.4"上恒成立$且仅当+!!")'$于是函数+!#"仅一个零点!
所以');满足条件! ,分…………………………………………………………………………
!("当'+;时$由于B!#")#;#*'在!!$.4"为增函数$
则B!!");*'('$当#&.4时$B!#"&.4!
则存在#'+!$使得B!#'")'$即使得+6!#'")'$
当!!$#'"时$+6!#'"('$当!#'$.4"时$+6!#'"+'$
所以+!#'"(+!!")'$且当#&.4时$+!#"&.4!
于是当!#'$.4"时存在+!#")'的另一解$不符合题意$舍去! !'分………………………
!)"当'('(;时$则B!#")#;#*'在!!$.4"为增函数$
又B!'")*'('$B!!");*'+'$
所以存在'(#'(!$使得B!#'")'$也就使得+6!#'")'$
当!'$#'"时$+6!#'"('$当!#'$!"时$+6!#'"+'$
所以+!#'"(+!!")'$且当#&'时$+!#"&.4!
于是在!'$#'"时存在+!#")'的另一解$不符合题意$舍去!
综上$'的取值范围为'#'或');! !#分………………………………………………………
选考题#!'分$
##!命题意图#本小题考查参数方程与极坐标方程$三角恒等变换等基础知识%考查核心素养的数
学运算$逻辑推理$应用意识!
解析#!!"由 #)#123!$
,)3/:.
/
0 !
!!为参数"$得曲线的普通方程为##
%.,#)!! #分…………………
将#)$123%$,)$3/:%代入$得%$#3/:#%.$#123#%)%$
即$#) %
$3/:#%.!$#) %
%3/:#%.123#%! "也可得分 ! +分…………………………………………
!#"由!!"知!
$# )$
%3/:#%.!
%$
设点 & 的极坐标为!$!$%"$因为C&*CD$则点D 的极坐标为 $#$%A!! "# ! 8分……………
所以"C&"#,"CD"#
"C&"#."CD"#) !
!
"C&"#. !
"CD"#
) !
!
$#
!
.!
$#
#
数学!理工类"试题答案 第 "!!!! 页!共"页"
) !
$
%3/:#%.!
%.$
%123#%.!
%
) !
$
%.!
#
)%
+! !'分………………………………………………………………………………
#$!命题意图#本小题考查基本不等式)不等式的证明方法)含绝对值的不等式等基本知识$考查
学生化归与转化等数学思想和推理论证等数学能力$以及逻辑推理)数学运算等能力!
解析#!!"由题
! #'槡 .!. #(槡 .!"#
)!#'.!".!#(.!".# #'槡 .!, #(槡 .!
#!#'.!".!#(.!".!#'.!".!#(.!"
)%!'.(".%
)!&$当且仅当')()$
#时取等号!
所以 #'槡 .!. #(槡 .!最大值为%> +分………………………………………………………
!#"由题$!
'.%
()!
$!'.(" !
'.%! "( )!
$ +.(
' .%'! "( ,!
$ +.# (
' ,%'槡! "( )$$当且仅当
(
' )%'
( $
'.(
.
/
0 )$
即')!$()#取等号$
所以$!
'.%
(的最小值为$!
又"#.#8"*"#*!"#"#8.!"$
不等式"#.#8"*"#*!"#!
'.%
(对任意#)& 恒成立$只需"#8.!"#$即可$
解得*##8#!$
即 8 的取值范围是**#$!+! !'分………………………………………………………………
书书书
数学命题报告 第 !!!!! 页!共"页"
数学科命题报告
一!指导思想
本次一诊考试试题命制主要依据!!"#$年普通高等学校招生全国统一考试大
纲"#!!"#$年普通高校招生全国统一考试数学试题"$全国!%"%#卷&'坚持(一体
四层四翼)的命题指导思想#针对(必备知识%关键能力%学科素养%核心价值)四层考
查内容以及(基础性%综合性%应用性%创新性)四个方面的考查要求#落实立德树人
根本任务#以诊断高三第一阶段复习成效为目的#从而正确引导各校下阶段复习
教学'
二!具体要求
#%本次考试范围与要求*试题分必考内容和选考内容'文科考生必考内容为
!课程标准"的必修内容和选修系列#和系列&内容#理科考生必考内容为!课程标
准"的必修内容和选修系列!和系列&内容'选考内容均为选修系列&的(坐标系
与参数方程)%(不等式选讲)等!个专题'
!%本次试题注重对数学思想方法的考查#注重对数学能力的考查#展现数学的
科学价值和人文价值#考查数学学科素养'同时兼顾试题的基础性%综合性和应用
性#重视试题间的层次性#合理调控综合程度#坚持多角度%多层次的考查'
'%主干知识重点考查'如函数与导数部分*对函数图象%函数性质%函数应用都
有所考查#应用导数解决函数最值问题#函数不等式等均有体现'又如三角函数与
解三角形部分#对三角函数的图象及其性质%诱导公式%三角函数定义等知识有所考
查#对正弦定理与余弦定理#以及利用两个定理解决实际问题均有体现'
&%考查学科素养和实现育人目标*
$#&强调综合能力的考查#重点是思维能力#而突破点是创新潜质#学科素养'
$!&考查能力三原则*考潜能%考思维%考应用'
数学命题报告 第 "!!!! 页!共"页"
$'&尽量体现!"#(版!普通高中课程方案和各学科课程标准"精神#一是全面落
实党的十八大和十九大精神+二是切实加强中华优秀传统文化和革命传统教育+三
是进一步强化了学科的育人功能'
$&&增加数学知识广度'本次试题尽量增加知识广度#拓展数学视野#让考生善
于发现知识联系#进而透析命题意图'
$)&突出试卷设计创新#优化试卷结构%创新设计理念%变换题型和设问方式%适
当改变试题的排列顺序#增强试题新颖性和灵活性#促进考生融会贯通%真懂会用#
引导中学数学全面教学%夯实基础%灵活学习%创新思考'
$*&试题背景新颖#尽量体现了(德%智%体%美%劳)五育并举的育人目标'
三!命题意图
详见参考答案中每小题的命题意图'