数学（文）卷·2018届湖北省部分重点中学上学期高二期末考试（2017-01） 9页

湖北省部分重点中学2016—2017 学年度上学期高二期末考试 数学试题（文科）‎ 命题人:武汉四中 汤闪 审题人:武汉四中 晏海燕 ‎ 一、选择题：本大题共12 小题，每小题5 分，共60 分. 在每小题给出的四个选项中，只有 一项是符合题目要求的.‎ ‎1．若命题“p∧q”为假，且为假，则（ ）.‎ A．“p∨q”为假 B．q为真 C．p为假 D．q为假 ‎2.已知是虚数单位，则复数的虚部是（ ）.‎ A． B． C． D．‎ ‎3.命题：“，”的否定是（　　）.‎ A. ， B. ，‎ C. ， D. ，‎ ‎4．“”是“方程表示椭圆”的( ) .‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不必要也不充分条件 ‎5．用反证法证明命题“设a，b为实数，则方程至少有一个实根”时，要做的假设是 ( ) . ‎ ‎ A．方程没有实根 ‎ ‎ B．方程至多有一个实根 ‎ ‎ C．方程至多有两个实根 ‎ ‎ D．方程恰好有两个实根 ‎6．命题“”为真命题的一个充分不必要条件是( ) .‎ ‎ A． B. C. D.‎ ‎7．下列命题错误的是（ ）.‎ ‎ A.在回归分析模型中,残差平方和越大,说明模型的拟合效果越好;‎ ‎ B.线性相关系数越大，两个变量的线性相关性越强；反之，线性相关性越弱；‎ ‎ C.由变量x和y的数据得到其回归直线方程: ,则一定经过 ‎ D.在回归直线方程中，当解释变量x每增加一个单位时，预报变量 ‎ 增加0.1个单位.‎ ‎8.下列命题错误的是( ). 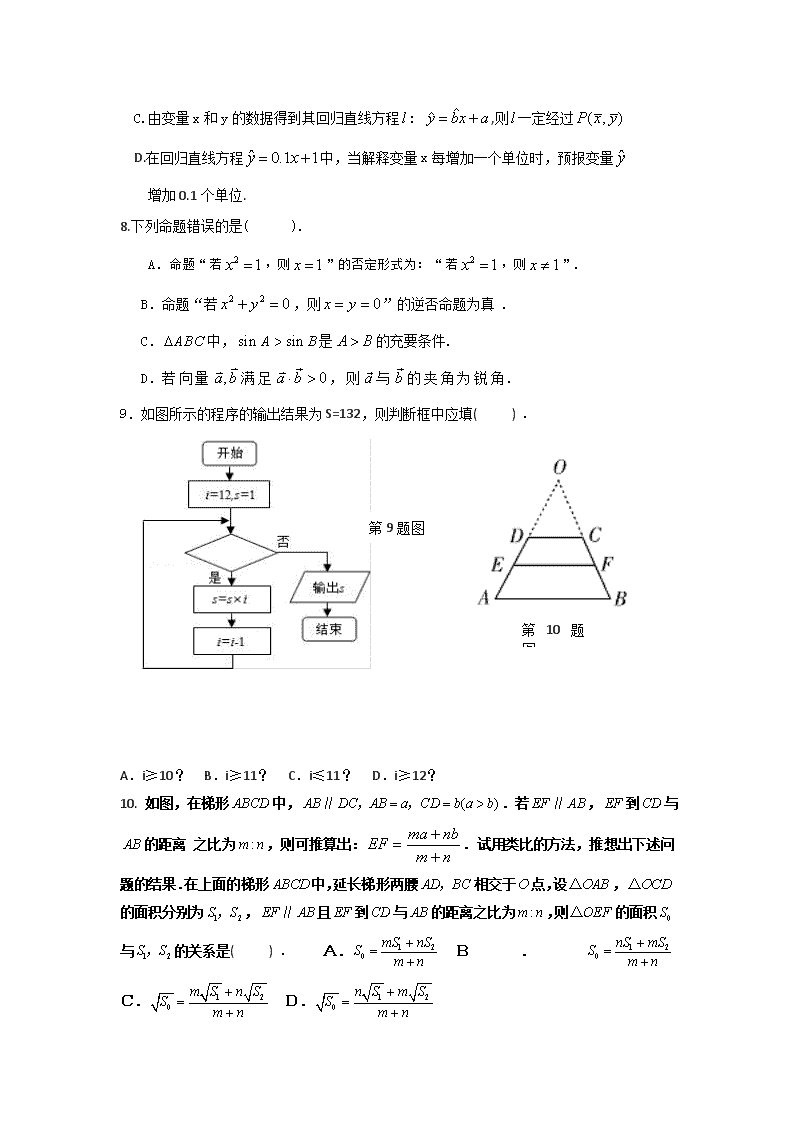‎ ‎ A．命题“若，则”的否定形式为：“若，则”.‎ ‎ B．命题“若，则”的逆否命题为真 .‎ ‎ C．中，是的充要条件.‎ ‎ D．若向量满足，则与的夹角为锐角.‎ ‎9．如图所示的程序的输出结果为S=132，则判断框中应填( ) . ‎ 第9题图 第10题图 ‎ ‎ ‎ ‎ ‎ ‎ A．i≥10？ B．i≥11？ C．i≤11？ D．i≥12？‎ ‎10. 如图，在梯形中，．若，到与的距离 之比为，则可推算出：．试用类比的方法，推想出下述问题的结果．在上面的梯形中，延长梯形两腰相交于点，设，的面积分别为，且到与的距离之比为，则的面积与的关系是( ) . Ａ． Ｂ． Ｃ． Ｄ．‎ ‎11.椭圆中，以点为中点的弦所在直线斜率为( ) .‎ ‎ A. B. C. D. ‎ ‎12. 若A点坐标为（1,1），F1是椭圆的左焦点，点P是该椭圆上的动点，则 ‎ 的最大值为( ) . ‎ ‎ A． B． C． D．‎ 二、填空题：本大题共 4 小题，每小题5 分，共20 分．请将答案填在答题卡对应题号的位，‎ 置上．答错位置，书写不清，模棱两可均不得分．‎ ‎13. 若命题“，使”是假命题，则实数a的取值范围为 ．‎ ‎14．下表是某地银行连续五年的储蓄存款（年底余额），假设储蓄存款关于年份的线性回归方程为 ，则= ．‎ ‎（，其中，）‎ 年份x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款y（千亿元）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ ‎15. 圆锥曲线中不同曲线的性质都是有一定的联系的,比如圆可以看成是特殊的椭圆,所以很多圆的性质结论可以类比到椭圆.例如:如图所示,椭圆C: 可以被认为由圆作纵向压缩变换或由圆作横向拉伸变换得到的.依据上述论述我们可以推出椭圆C的面积公式为 ．‎ ‎16. 已知椭圆E的左、右焦点分别为F1、F2，过F1且斜率为2的直线交椭圆E于P、Q两 点，若△PF1F2为直角三角形，则椭圆E的离心率为________．‎ 三、解答题：本大题共5 小题，共70 分． 解答应写出文字说明、证明过程或演算步骤．‎ ‎17. （本小题满分10分） (1)已知,求;‎ ‎ (2)已知是关于x的一元二次实系数方程的一个根，求实数的值.‎ ‎18. （本小题满分12分）求分别满足下列条件的椭圆C的标准方程.‎ ‎ （1）过点且与椭圆有相同焦点.‎ ‎ ( 2 )中心为原点，焦点在x轴上，离心率为，过的直线交椭圆C于A、B两点，‎ ‎ 且△的周长为16，求椭圆C的标准方程. ‎ ‎19．（本小题满分12分）命题P：函数有意义,‎ 命题q: 实数x满足.‎ ‎ (1)当且为真，求实数x的取值范围；‎ ‎（2）若是的充分不必要条件，求实数的取值范围.‎ ‎20．(本小题满分12 分) 对武汉市工薪阶层关于“楼市限购政策”的态度进行调查，随机抽查了50人，他们月收入（单位：百元）的频数分布及对“楼市限购政策”赞成人数如下表：‎ 月收入(百元)‎ ‎[15,25)‎ ‎[25,35)‎ ‎[35,45)‎ ‎[45,55)‎ ‎[55,65)‎ ‎[65,75)‎ 频数 ‎5‎ ‎10‎ ‎15‎ ‎10‎ ‎5‎ ‎5‎ 赞成人数 ‎3‎ ‎8‎ ‎12‎ ‎4‎ ‎2‎ ‎1‎ ‎(1)从这50人是否赞成“楼市限购政策”采取分层抽样，抽取一个容量为10的样本，问样本中 赞成与不赞成“楼市限购政策”的人数各有多少名？‎ ‎(2)根据以上统计数据填写下面22的列联表，并回答是否有95%的把握认为月收入以55百元为 分界点对“楼市限购政策”的态度有差异？‎ 月收入低于55百元人数 月收入不低于55百元人数 合计 赞成 a=‎ b=‎ 不赞成 c=‎ d=‎ 合计 ‎（参考公式：，其中）‎ P（）‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎21．(本小题满分12分)‎ 已知数列的前项和为，，满足．‎ ‎（Ⅰ）计算，猜想的一个表达式（不需要证明）‎ ‎（Ⅱ）设，数列的前项和为，求证：．‎ ‎22．（本小题满分12 分)‎ 如图，已知椭圆的离心率是，一个顶点是．‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）设，是椭圆上异于点的任意两点，且．试问：直线是否恒过一定点？若是，求出该定点的坐标；若不是，说明理由．‎ 湖北省部分重点中学2016-2017学年度上学期高二期末考试 数学试卷参考答案(文科)‎ 一、 选择题DABB ACAD BCDC ‎ 二、填空题13. 14. 1.2 15. 16. 或 ‎ 三、解答题 ‎17 .（1），‎ 另解，…5分 ‎ （2）代入方程中，得到.‎ ‎ 即且，解得.‎ 另解亦为方程的解，由韦达定理可知 ‎， ，解得. …10分 ‎ 18. 解：（1）在椭圆中.‎ 设椭圆方程为，代入点（3，-2），即，…3分 解得, …6分[]‎ ‎（2）解：设椭圆的标准方程为： ‎ 据题意,，…8分 ‎. …12分 ‎19.(1) 若为真，则p真q真.‎ ‎ 当，命题p为真，则，即，即 .‎ ‎ 命题q为真，则,故为真，x的取值范围是…6分 ‎ （2）是的充分不必要条件，则q是p的充分不必要条件.‎ ‎ 则命题p为真，则，即，命题q为真，.‎ ‎ ,,即的取值范围为.…12分 ‎20.(1)50人中有30人赞成，故抽取10人的样本，其中6人赞成，4人不赞成。…6分 ‎ （2）‎ 月收入低于55百元人数 月收入不低于55百元人数 合计 赞成 a=27‎ b=3‎ ‎30‎ 不赞成 c=13‎ d=7‎ ‎20‎ 合计 ‎40‎ ‎10‎ ‎50‎ ‎=‎ 有95%的把握认为月收入以55百元为分界点对“楼市限购政策”的态度有差异. …12分 ‎21、（1）因为，所以，由此整理得，于是有：，猜想：…6分 ‎（2）由（1），于是：‎ ‎…10分 又因为，所以． …12分 ‎22. （Ⅰ）解：设椭圆的半焦距为．依题意，得 ‎， ， …3分 ‎ 解得 ,所以，椭圆的方程是． …5分 ‎ ‎（Ⅱ）证法一：易知，直线的斜率存在，设其方程为． ‎ 将直线的方程代入，‎ 消去，整理得 ． …7分 ‎ 设 ，，则 ，．…9分 因为 ，且直线的斜率均存在，‎ 所以 ， 整理得 ．（2） ‎ 因为 ，，‎ 所以 ，．（3）‎ 将（3）代入（2），整理得 ‎ ．（4） …10分 ‎ 将（1）代入（4），整理得 ． …12分 ‎ 解得 ，或（舍去）．‎ 所以，直线恒过定点． ‎ 证法二：直线的斜率均存在，设直线的方程为． …6分 将直线的方程代入，消去，得 ． ‎ 解得 ，或． ‎ 设 ，所以，， ‎ 所以 ． ‎ 以替换点坐标中的，可得 ． ‎ 从而，直线的方程是 ． ‎ 依题意，若直线过定点，则定点必定在轴上． ‎ 在上述方程中，令，解得．‎ 所以，直线恒过定点． …12分