- 168.00 KB
- 2023-05-05 发布
第13课时 一次函数
【课前展练】
1. 已知函数:①y=-x,②y= ,③y=3x-1,④y=3x2,⑤y= ,⑥y=7-3x中,正比例函数有 ,一次函数有
2. 若正比例函数(≠)经过点(,),则该正比例函数的解析式为________.
3.如图,一次函数的图象经过A、B两点,
则关于x的不等式的解集是 .
4. 一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的解析式可以是 .(任写出一个符合题意即可)
5.两个一次函数y1=mx+n.y2=nx+n,它们在同一坐标系中的图象可能是图中的( )
6. 生物学研究表明:某种蛇的长度y(㎝)是其尾长x(cm)的一次函数,当蛇的尾长为6cm时,蛇长为45.5㎝;当蛇的尾长为14cm时,蛇长为105.5㎝;当蛇的尾长为10cm时,蛇长为_________㎝;
【要点提示】利用题设中所给条件:两组变量的值;图象上两个点的坐标;直线在坐标轴上的截距;直线与坐标围成图形的面积;两直线的平行关系等求一次函数的解析式;根据一次函数的图象特征、性质不画函数图象确定一次函数图象所经过的象限,增减性以及k,b的取值范围;根据实际问题中的条件写出函数解析式,并能依据实际问题确定自变量的取值范围;运用函数的相关知识优化设计、确定最佳方案
【考点梳理】
1.正比例函数的一般形式是__________.一次函数的一般形式是__________________.
2. 一次函数的图象是经过 和 两点的 .
3. 求一次函数的解析式的方法是 ,其基本步骤是:⑴ ;
⑵ ; ⑶ ;⑷ .
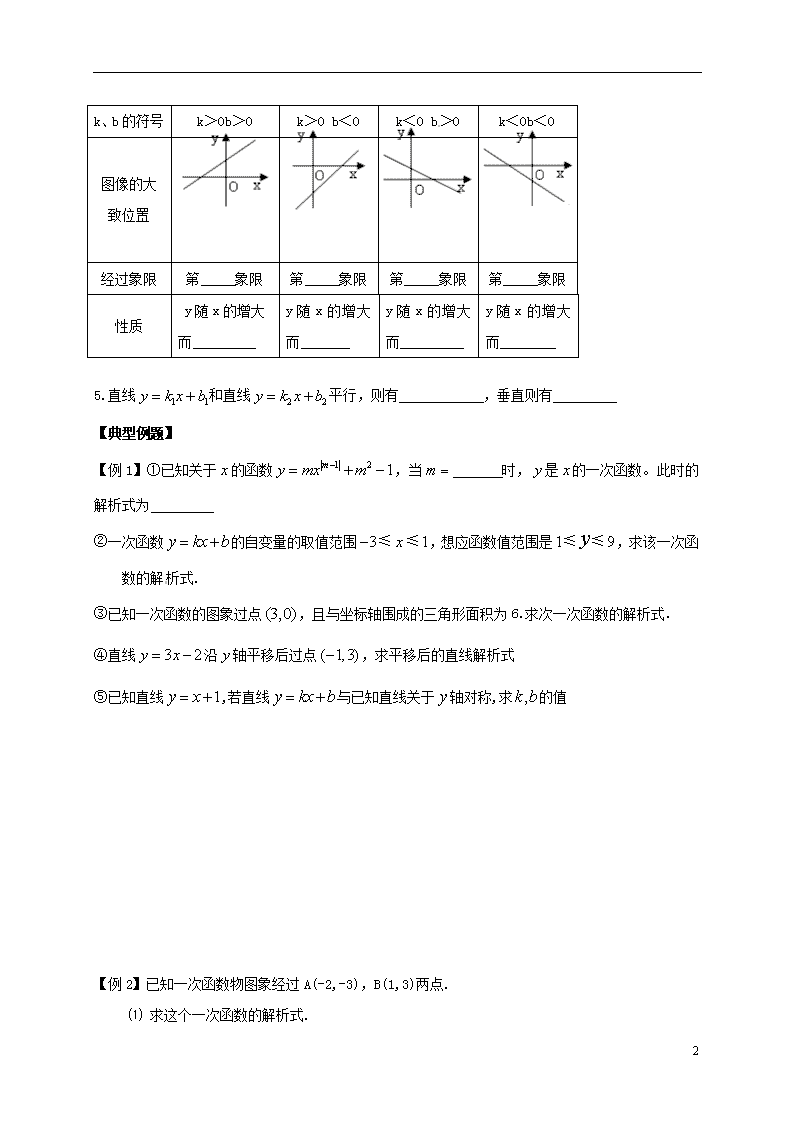
4.一次函数的图象与性质
3
k、b的符号
k>0b>0
k>0 b<0
k<0 b>0
k<0b<0
图像的大致位置
经过象限
第 象限
第 象限
第 象限
第 象限
性质
y随x的增大
而
y随x的增大而
y随x的增大而
y随x的增大而
5.直线和直线平行,则有 ,垂直则有
【典型例题】
【例1】①已知关于的函数,当 时,是的一次函数。此时的解析式为
②一次函数的自变量的取值范围≤≤,想应函数值范围是≤≤,求该一次函数的解析式.
③已知一次函数的图象过点,且与坐标轴围成的三角形面积为6.求次一次函数的解析式.
④直线沿轴平移后过点,求平移后的直线解析式
⑤已知直线,若直线与已知直线关于轴对称,求的值
【例2】已知一次函数物图象经过A(-2,-3),B(1,3)两点.
⑴ 求这个一次函数的解析式.
3
⑵ 试判断点P(-1,1)是否在这个一次函数的图象上.
⑶ 求此函数与x轴、y轴围成的三角形的面积.
【例3】在平面直角坐标系中,有两点,现另取一点,当 时,的值最小.
(孝感2009)
【小结】1.求一次函数的解析式y=kx+b的基本方法是待定系数法,通过题设中的条件转化为①两组变量的值;②两个点的坐标,均可求出一次函数的解析式.
2.利用一次函数的相关知识解决实际问题是中考命题的趋势.而一次函数的定义、性质是解决好实际问题的基础,依据实际问题中的相互关系正确写出函数关系式是解题的关键.
3