- 258.00 KB
- 2021-06-26 发布
黑龙江省大庆实验中学2019-2020学年高二下学期第五次网上检测数学文
1.设i为虚数单位,则复数(1+i)2=( )
A.0
B.2
C.2i
D.2+2i
答案:C
[(1+i)2=1+2i+i2=2i.]
2.复数=( )
A.i
B.1+i
C.-i
D.1-i
答案:A
[法一:===i. 法二:===i.]
3.根据给出的程序框图,计算f(-1)+f(2)=( )
图911
A.0
B.1
C.2
D.4
答案:A
[f(-1)=4×(-1)=-4,f(2)=22=4,∴f(-1)+f(2)=-4+4=0.]
4.已知i为虚数单位,复数z=的虚部为( )
A.-
B.-
C.
D.
答案:D
复数z====+i,则其虚部为,故选D.
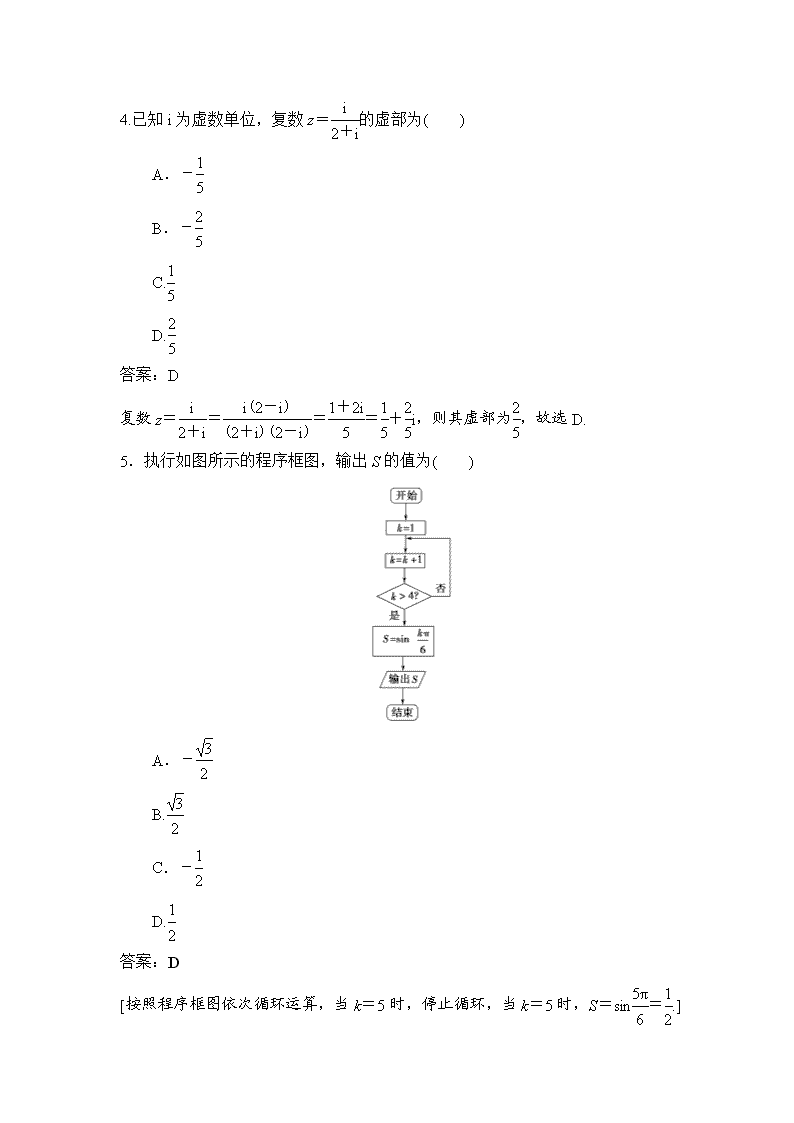
5.执行如图所示的程序框图,输出S的值为( )
A.-
B.
C.-
D.
答案:D
[按照程序框图依次循环运算,当k=5时,停止循环,当k=5时,S=sin=
eq f(1,2).]
6.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
A.7
B.12
C.17
D.34
答案:C
[输入x=2,n=2.第一次,a=2,s=2,k=1,不满足k>n;
第二次,a=2,s=2×2+2=6,k=2,不满足k>n;
第三次,a=5,s=6×2+5=17,k=3,满足k>n,输出s=17.]
7.设z=+i,则|z|=( )
A.
B.
C.
D.2
答案:B
z=+i=+i=+i,|z|==.
8.定义运算=ad-bc,则符合条件=0的复数z对应的点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:A
[由题意得z×1-2(1+i)=0,则z=2+2i在复平面内对应的点为(2,2),位于第一象限,故选A.]
9.执行如图所示的程序框图,输出的s值为( )
图916
A.8
B.9
C.27
D.36
答案:B
k=0,s=0,满足k≤2;s=0,k=1,满足k≤2;s=1,k=2,满足k≤2;
s=1+23=9,k=3,不满足k≤2,输出s=9.
10.我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
A.4
B.5
C.2
D.3
答案:A
该程序框图运行4次,第1次循环,a=1,A=1,S=2,n=1;第2次循环,a=,A=2,S=,n=2;第3次循环,a=,A=4,S=,n=3;第4次循环,a=,A=8,S=,n=4,此时循环结束,则输出的n=4,故选A.
11.执行如图所示的程序框图,若输出k的值为8,则判断框内可填入的条件是( )
图9110
A.s≤?
B.s≤?
C.s≤?
D.s≤?
答案:C [执行第1次循环,则k=2,s=,满足条件.
执行第2次循环,则k=4,s=+=,满足条件.
执行第3次循环,则k=6,s=+=,满足条件.执行第4次循环,k=8,s=+=,不满足条件,输出k=8,因此条件判断框应填s≤?.
12.已知复数z=1+,则1+z+z2+…+z2019=( )
A.1+i
B.1-i
C.i
D.0
答案:D
[z=1+=1+=i,∴1+z+z2+…+z2019====0.]
13.执行下面的程序框图,如果输入的a=4,b=6,那么输出的n=( )
A.3
B.4
C.5
D.6
答案:B
[开始a=4,b=6,n=0,s=0.
第1次循环:a=2,b=4,a=6,s=6,n=1;
第2次循环:a=-2,b=6,a=4,s=10,n=2;
第3次循环:a=2,b=4,a=6,s=16,n=3;
第4次循环:a=-2,b=6,a=4,s=20,n=4.
此时,满足条件s>16,退出循环,输出n=4.故选B.]
14.如图所示的程序框图,如果输入n=3,则输出的S= ( )
A.
B.
C.
D.
答案:B
[第一次循环:S=,i=2;
第二次循环:S=+,i=3;
第三次循环:S=++,i=4,满足循环条件,结束循环.
故输出S=++
==,故选B.]
15.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )
A.0
B.2
C.4
D.14
答案:B
[a=14,b=18.
第一次循环:14≠18且14<18,b=18-14=4;
第二次循环:14≠4且14>4,a=14-4=10;
第三次循环:10≠4且10>4,a=10-4=6;
第四次循环:6≠4且6>4,a=6-4=2;
第五次循环:2≠4且2<4,b=4-2=2;
第六次循环:a=b=2,跳出循环,输出a=2,故选B.]
16.设f(n)=n+n(n∈N*),则集合{f(n)}中元素的个数为( )
A.1
B.2
C.3
D.无数个
答案:C
[f(n)=n+n=in+(-i)n,
f(1)=0,f(2)=-2,f(3)=0,f(4)=2,f(5)=0,…,
∴集合中共有3个元素.]
17.在平面直角坐标系xOy中,曲线C的参数方程为(α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin=.
(1)求C的普通方程和l的倾斜角;
(2)设点P(0,2),l和C交于A,B两点,求|PA|+|PB|.
[解] (1)由消去参数α,得+y2=1,
即C的普通方程为+y2=1.2分
由ρsin=,得ρsin θ-ρcos θ=2,(*)
将代入(*),化简得y=x+2,
所以直线l的倾斜角为.4分
(2)由(1)知,点P(0,2)在直线l上,可设直线l的参数方程为(t为参数),
即(t为参数),
代入+y2=1并化简,得5t2+18t+27=0,
Δ=(18)2-4×5×27=108>0,8分
设A,B两点对应的参数分别为t1,t2,
则t1+t2=-<0,t1t2=>0,所以t1<0,t2<0,
所以|PA|+|PB|=|t1|+|t2|=-(t1+t2)=.10分