- 177.00 KB
- 2021-06-26 发布
24.4.1 解直角三角形
【学习目标】
1.巩固勾股定理,熟悉运用勾股定理。
2.学会运用三角函数解直角三角形。
3.掌握解直角三角形的几种情况。
【学习重难点】
1.使学生养成“先画图,再求解”的习惯。
2.运用三角函数解直角三角形。
【学习过程】
一、课前准备
1.在三角形中共有几个元素?
2.直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
(1)边角之间关系
如果用表示直角三角形的一个锐角,那上述式子就可以写成.
(2) 三边之间关系 (3)锐角之间关系
(勾股定理)
二、学习新知
自主学习:
我们已经掌握了直角三角形边角之间的各种关系,这些都是解决与直角三角形有关的实际问题的有效工具.
例1 如图所示,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处.大树在折断之前高多少?
4
解 利用勾股定理可以求出折断倒下部分的长度为
13+5=18(米).
所以,大树在折断之前高为18米.
在例1中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.像这样,在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
解直角三角形只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角.
实例分析:
例1、如图所示,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处.大树在折断之前高多少?
解:
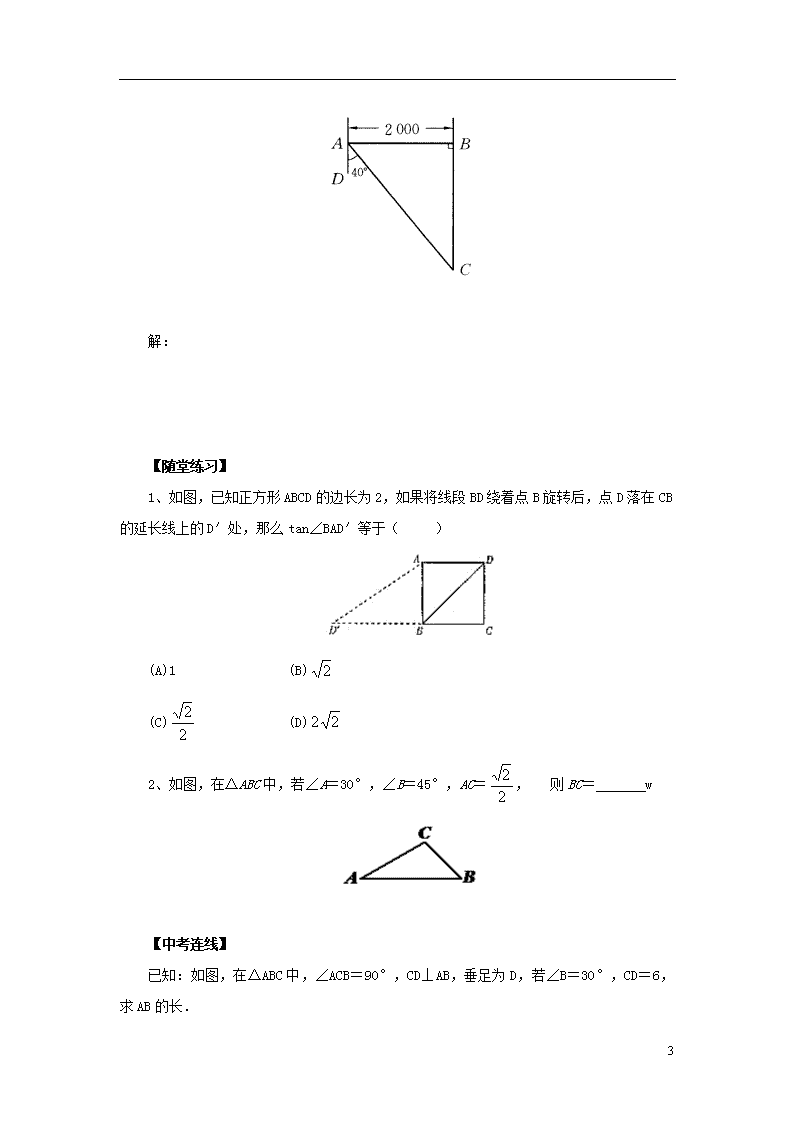
例2、如图,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)
4
解:
【随堂练习】
1、如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′等于( )
(A)1 (B)
(C) (D)
2、如图,在△ABC中,若∠A=30°,∠B=45°,AC=, 则BC= w
【中考连线】
已知:如图,在ΔABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
4
【参考答案】
随堂练习
1、B 2、
中考连线
8
4
相关文档
- 解直角三角形的应用中考练习题2021-06-25 20:57:0817页
- 2020届中考数学全程演练 第二部分 2021-06-23 22:02:356页
- 2020九年级数学下册 第1章 解直角2021-06-23 20:42:095页
- 2020九年级数学上册 第24章 解直角2021-06-23 14:42:266页
- 九年级下册数学教案 1-4 解直角三2021-06-22 02:21:254页
- 中考数学全程复习方略微专题七解直2021-06-21 16:27:1035页
- 2020九年级数学下册 第1章 解直角2021-06-19 18:27:126页
- 2020九年级数学下册 第1章 解直角2021-06-07 20:10:494页
- 九年级下册数学教案28-2-2 第3课时2021-06-04 03:02:324页
- 2019九年级数学上册 第24章 解直角2021-06-04 01:01:242页