- 1.21 MB
- 2021-06-25 发布
南昌三中2016-2017学年度下学期期中考试
高二数学(文)试卷
命题:张金生 审题:徐哓东
一、选择题(本大题共12小 题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项符合题目要求)
1、下列图形中不一定是平面图形的是( )
A,三角形 B.四边相等的四边形 C.梯形 D.平行四边形
2.校教职成员、教师、后勤人员、理科教师、文科教师的结构图正确的是( )
3.已知点M的极坐标为,下列所给出的四个坐标中,也能表示点M的极坐标的是( )
A. B. C. D.
4.和是两个不重合的平面,在下列条件中可判定平面和平行的是( )。
A. 和都垂直于同一平面
B. 内不共线的三点到的距离相等
C. 是平面内的直线且
D. 是两条异面直线且
5.若<<0,则下列结论不正确的是 ( )
A.a2<b2 B.ab<b2 C.+>2 D.|a|-|b|=|a-b|
6.函数在上不单调,则的取值范围是( )
A. B. C. D.
7.方程表示的曲线是( )
A. 双曲线 B.双曲线的上支 C.双曲线的下支 D.圆
8
.对一批产品的长度(单位:毫米)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35)上为三等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )
A.0.09 B.0.20 C.0.25 D.0.45
9.中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器———商鞅铜方升,其三视图如图所示(单位:寸),若取3,其体积为12.6(立方寸),则图中的为( )
A.1.2 B.1.6 C.1.8 D.2.4
10.如右上图,正方体的棱线长为1,线段上有两个动点E,F,且,则下列结论中错误的是( )
A. B.
C.三棱锥的体积为定值 D.异面直线所成的角为定值
11.已知双曲线的焦距为,且双曲线的一条渐近线与直线垂直,则双曲线的方程为( )
A. B. C. D.
12.已知函数()恰有两个极值点,(其中),且,则的取值范围是( )
A. B. C. D.
二.填空题(本大题共5小题,每小题4分,共20分) [来源:学科网ZXXK]
13.已知关于x的不等式|x-1|+|x|≤k无解,求实数k的取值范围_________;
14.动圆M过点F(0,2)且与直线y=-2相切,则圆心M的轨迹方程是 .
15.某商场为了了解某品牌羽绒服的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,数据如下表:
月平均气温x(℃)
17
13
8
2
月销售量y(件)
24
33
40
55
由表中数据算出线性回归方程=bx+a中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月羽绒服的销售量约为________件.
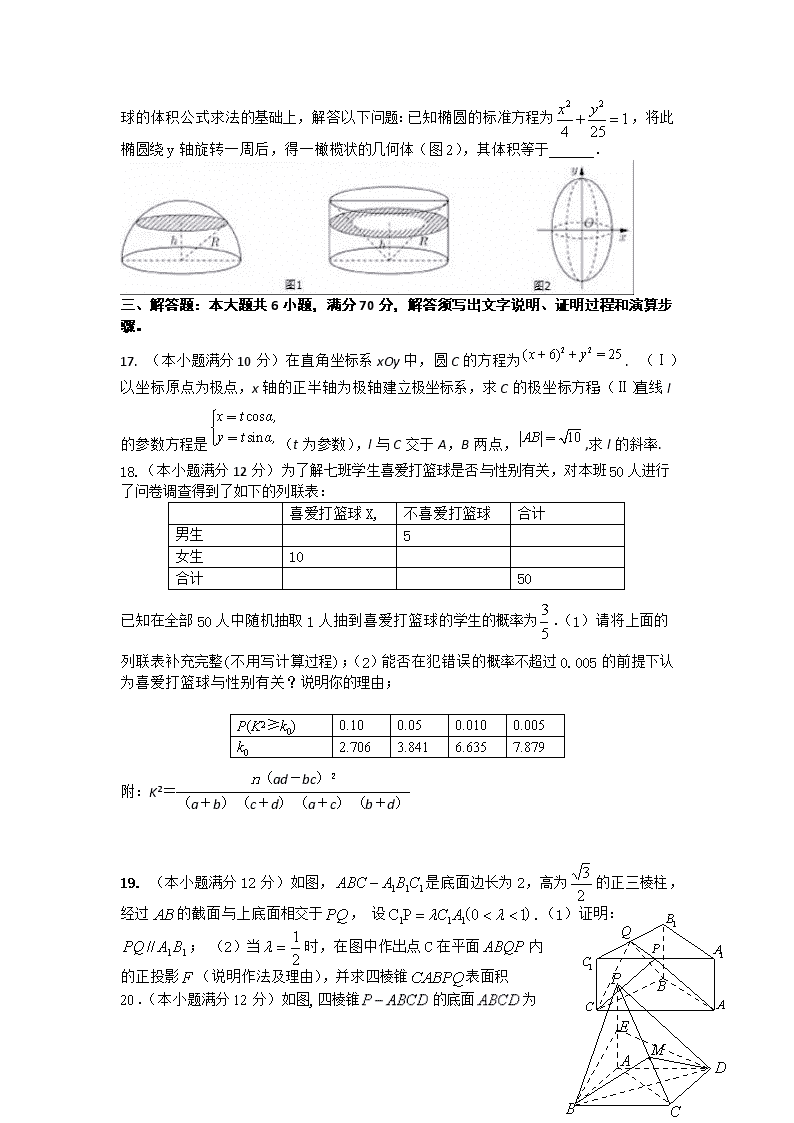
16.现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程和演算步骤。
17. (本小题满分10分)在直角坐标系xOy中,圆C的方程为.(Ⅰ)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求C的极坐标方程;(Ⅱ)直线l的参数方程是(t为参数),l与C交于A,B两点,,求l的斜率.
18.(本小题满分12分)为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球X,
不喜爱打篮球
合计
男生
5
女生
10
合计
50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.(1)请将上面的列联表补充完整(不用写计算过程);(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
P(K2≥k0)
0.10
0.05
0.010
0.005
k0
2.706
3.841
6.635
7.879
附:K2=
19. (本小题满分12分)如图,是底面边长为2,高为的正三棱柱,经过的截面与上底面相交于, 设.(1)证明:; (2)当时,在图中作出点C在平面内的正投影(说明作法及理由),并求四棱锥表面积
20.(本小题满分12分)如图,四棱锥的底面为菱形,,底面,,为的中点.(1)求证:平面;(2) 在侧棱上是否存在一点
,满足平面,若存在,求的长;若不存在,说明理由.(3)求三棱锥的体积;
21.(本小题满分12分)已知函数.(I)当时,求曲线在处的切线方程;(II)若当时,恒成立,求的取值范围.
O
x
y
22.(本小题满分12分)达∙芬奇椭圆仪是一种画椭圆的工具,它是由十字形滑槽和长杆构成,上的栓子可沿滑槽上下往复滑动,栓子可沿滑槽左右往复滑动,处的笔尖随、的滑动画出的图形即为椭圆.已知,,以十字形滑槽的交点为原点,建立平面直角坐标系.(Ⅰ)求椭圆的方程;(Ⅱ)已知过椭圆的右焦点的直线交椭圆于、两点,过原点的直线 交椭圆于、两点,且,试问是否为定值?若是定值,求出此定值;若不是,说明理由.
南昌三中2016-2017学年度下学期期中考试
高二数学(文)答案
一、选择题(本大题共12小 题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项符合题目要求)
1、下列图形中不一定是平面图形的是(B )
A,三角形 B.四边相等的四边形 C.梯形 D.平行四边形
2.校教职成员、教师、后勤人员、理科教师、文科教师的结构图正确的是( A )
3.已知点M的极坐标为,下列所给出的四个坐标中,也能表示点M的极坐标的是( )
A. B. C. D.
【答案】D
4.和是两个不重合的平面,在下列条件中可判定平面和平行的是( D )。
A. 和都垂直于同一平面 B. 内不共线的三点到的距离相等
C. 是平面内的直线且
D. 是两条异面直线且
5.若<<0,则下列结论不正确的是 ( D )
A.a2<b2 B.ab<b2 C.+>2 D.|a|-|b|=|a-b|
6.函数在上不单调,则的取值范围是( D )
A. B. C. D.
7.方程表示的曲线是( )
A. 双曲线 B.双曲线的上支 C.双曲线的下支 D.圆
【答案】B. 【解析】两个等式两边分别平方,再相减,得即有,又,可见与以上参数方程等价的普通方程为.显然它表示焦点在轴上,以原点为中心的双曲线的上支,选B.
8.对一批产品的长度(单位:毫米)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35)上为三等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )
A.0.09 B.0.20 C.0.25 D.0.45
答案 D解析 由图可知抽得一等品的概率为0.3,抽得三等品的概率为0.25,则抽得二等品的概率为1-0.3-0.25=0.45.
9.中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器———商鞅铜方升,其三视图如图所示(单位:寸),若取3,其体积为12.6(立方寸),则图中的为( )
A.1.2 B.1.6 C.1.8 D.2.4
解:B.
10.如右上图,正方体的棱线长为1,线段上有两个动点E,F,且,则下列结论中错误的是( )
A. B.
C.三棱锥的体积为定值 D.异面直线所成的角为定值
11.已知双曲线的焦距为,且双曲线的一条渐近线与直线垂直,则双曲线的方程为( )
A. B. C. D.
【答案】A
12.已知函数()恰有两个极值点,(其中),且,则的取值范围是(C)
A. A. B. C. D.
解:令,则方程有两不等实根,即直线与函数的图像有两个交点,易得其中一个交点为,而,,
当直线与函数的图像相切于点时,,即
故由图像知,的取值范围是,故选C.
二.填空题(本大题共5小题,每小题4分,共20分) [来源:学科网ZXXK]
13.已知关于x的不等式|x-1|+|x|≤k无解,求实数k的取值范围_________;
14.动圆M过点F(0,2)且与直线y=-2相切,则圆心M的轨迹方程是 x2=8y .
15.某商场为了了解某品牌羽绒服的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,数据如下表:
月平均气温x(℃)
17
13
8
2
月销售量y(件)
24
33
40
55
由表中数据算出线性回归方程=bx+a中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月羽绒服的销售量约为________件.46
16.现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
解:椭圆的长半轴为5,短半轴为2,现构造一个底面半径为2,高为5的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,根据祖暅原理得出椭球的体积V=2(V圆柱﹣V圆锥)=2(π×22×5﹣)=.
故答案为:.
三、解答题:本大题共6小题,满分75分,解答须写出文字说明、证明过程和演算步骤。
17. (本小题满分10分)在直角坐标系xOy中,圆C的方程为.(Ⅰ)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求C的极坐标方程;(Ⅱ)直线l的参数方程是(t为参数),l与C交于A,B两点,,求l的斜率.
【答案】(Ⅰ);(Ⅱ).
【解析】(I)由可得的极坐标方程
(II)在(I)中建立的极坐标系中,直线的极坐标方程为
由所对应的极径分别为将的极坐标方程代入的极坐标方程得
于是
由得,所以的斜率为或.
18.(本小题满分12分)为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球X,
不喜爱打篮球
合计
男生
5
女生
10
合计
50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.(1)请将上面的列联表补充完整(不用写计算过程);(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
P(K2≥k0)
0.10
0.05
0.010
0.005
k0
2.706
3.841
6.635
7.879
附:K2=
解:(1)
喜爱打篮球X,
不喜爱打篮球
合计
男生
20
5
25
女生
10
15
25
合计
30
20
50
(5分)
(2) 由列联表得
所以能在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关(12分)
19. (本小题满分12分)如图,是底面边长为2,高为的正三棱柱,经过的截面与上底面相交于, 设.(1)证明:; (2)当时,在图中作出点C在平面内的正投影(说明作法及理由),并求四棱锥表面积
19. 【解析】:(I)∵平面平面,平面平面,平面平面,,,又. (5分)
(Ⅱ)点是中点,理由如下:
当时,分别是的中点,连接和, 因为
是正三棱柱,所以, (6分)
取中点,连接在等腰梯形中,,
连接中,,
平面ABF,即, (9分)
所以点是在平面内的正投影。
(12分)
20.(本小题满分12分)如图,四棱锥的底面为菱形,,底面,,为的中点.(1)求证:平面;(2) 在侧棱上是否存在一点,满足平面,若存在,求的长;若不存在,说明理由.(3)求三棱锥的体积;
(1)证明:设、相交于点,连结, 底面为菱形,为的中点,
又为的中点, 又平面,平面,
平面
(Ⅱ) 解:因为底面,所以, 又底面为菱形,, ,平面,平面,
平面, 在内,易求,,
在平面内,作,垂足为, 设,则有,解得 连结,,,,平面, 平面,平面. 所以满足条件的点存在,此时的长为
(3)因为底面为菱形,,所以是边长为正三角形,
又因为底面,所以为三棱锥的高,
21.(本小题满分12分)已知函数.(I)当时,求曲线
在处的切线方程;(II)若当时,恒成立,求的取值范围.
试题解析:(I)的定义域为.当时,,曲线在处的切线方程为
(II)当时,等价于令,则
,
(i)当,时,,故在上单调递增,因此;
(ii)当时,令得,
由和得,故当时,,在单调递减,因此.综上,的取值范围是
22.(本小题满分12分)达∙芬奇椭圆仪是一种画椭圆的工具,它是由十字形滑槽和长杆构成,上的栓子可沿滑槽上下往复滑动,栓子可沿滑槽左右往复滑动,处的笔尖随、的滑动画出的图形即为椭圆.已知,,以十字形滑槽的交点为原点,建立平面直角坐标系.(Ⅰ)求椭圆的方程;(Ⅱ)已知过椭圆的右焦点的直线交椭圆于、两点,过原点的直线 交椭圆于、两点,且,试问是否为定值?若是定值,求出此定值;若不是,说明理由.
O
x
y
解:(Ⅰ)设,,,则由已知可得:
为的中点,,即……2分
又,,,即椭圆的方程为………5分
(Ⅱ)①当直线的斜率为0时,,,…6分
②当直线的斜率不为0时,设直线的方程为,则直线的方程为,设,,,
联立方程,消去得,则,…8分
联立,消去得,,
由椭圆的对称性可得………10分
综上所述为定值……12分