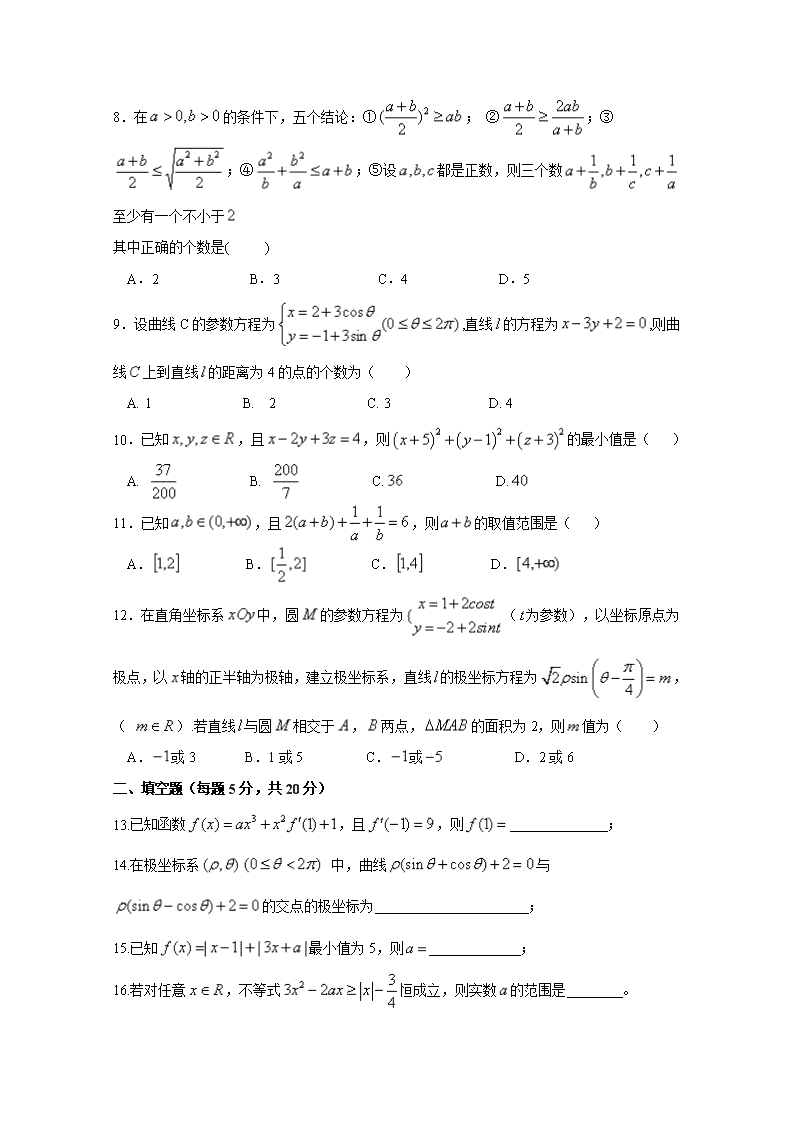- 598.00 KB
- 2021-06-25 发布
哈尔滨市第六中学2020届4月份阶段性测试
高二理科数学试题
一、选择题(每题5分,共60分)
1. 是成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2. 在同一平面直角坐标系中,经过伸缩变换后,曲线变为曲线,则曲线的方程为( )
A. B. C. D.
3. 直线分别与轴,轴交于,两点,点在圆上,则面积的取值范围是
A. B. C. D.
4.设曲线在点处的切线方程为,则( )
A.3 B. C.4 D.
5.已知函数,且,则的值是( )
A. B. C. D.
6.已知直线的参数方程为 ,则直线的倾斜角为( )
A. B. C. D.
7.已知直线:(为参数)和抛物线:,与分别交于点,则点到两点距离之和是( )
A.10 B. C. D.
8.在的条件下,五个结论:①; ②;③;④;⑤设都是正数,则三个数至少有一个不小于
其中正确的个数是( )
A.2 B.3 C.4 D.5
9.设曲线C的参数方程为,直线的方程为,则曲线上到直线的距离为4的点的个数为( )
A. 1 B. 2 C. 3 D. 4
10.已知,且,则的最小值是( )
A. B. C. D.
11.已知,且,则的取值范围是( )
A. B. C. D.
12.在直角坐标系中,圆的参数方程为(为参数),以坐标原点为极点,以轴的正半轴为极轴,建立极坐标系,直线的极坐标方程为,( ).若直线与圆相交于,两点,的面积为2,则值为( )
A.或3 B.1或5 C.或 D.2或6
二、填空题(每题5分,共20分)
13.已知函数,且,则 ;
14.在极坐标系 中,曲线与的交点的极坐标为 ;
15.已知最小值为5,则 ;
16.若对任意,不等式恒成立,则实数的范围是 。
三、解答题(共70分)
17.(共10分)设函数
(1)解不等式
(2)若在上有实数解,求的取值范围.
18.(共12分)平面直角坐标系中,是过定点且倾斜角为的直线,在极坐标系(以坐标原点为极点,以轴非负半轴为极轴,取相同单位长度)中,曲线的极坐标方程为 .
(1)写出直线的参数方程,并将曲线的方程为化直角坐标方程;
(2)若曲线与直线相交于不同的两点,求的取值范围。
19.(共12分)已知函数,且的解集为
(1)求的值;
(2)若均为正数,且,求①的最大值;②的最大值.
20.(共12分)已知椭圆: (为参数),是上的动点,且满足(为坐标原点),以原点为极点,以轴的正半轴为极轴建立极坐标系,点的极坐标为
(1)求线段的中点的轨迹的普通方程;
(2)证明:为定值,并求面积的最大值。
21.(共12分)已知三棱柱中,三个侧面均为矩形,底面为等腰直角三角形, ,点为棱的中点,点在棱上运动.
(I)求证;
(II)当点运动到某一位置时,恰好使二面角的平面角的余弦值为,求点到平面的距离;
(III)在(II)的条件下,试确定线段上是否存在一点,使得平面?若存在,确定其位置;若不存在,说明理由.
22.(共12分)随着快递行业的崛起,中国快递业务量惊人,年中国快递量世界第一,已连续五年突破五百亿件,完全超越美日欧的总和,稳居世界第一名.某快递公司收取费的标准是:不超过的包裹收费元;超过的包裹,在元的基础上,每超过(不足,按计算)需再收元.
该公司将最近承揽(接收并发送)的件包裹的质量及件数统计如下(表):
表:
公司对近天每天承揽包裹的件数(在表中的“件数范围”内取的一个近似数据)、件数范围及天数,列表如下(表):
表:
(1)将频率视为概率,计算该公司未来天内恰有天揽件数在之间的概率;
(2)①根据表中最近件包裹的质量统计,估计该公司对承揽的每件包裹收取快递费的平均值:
②根据以上统计数据,公司将快递费的三分之一作为前台工作人员的工资和公司利润,其余用作其他费用.目前,前台有工作人员人,每人每天揽件数不超过件,日工资元.公司正在考虑是否将前台人员裁减人,试计算裁员前、后公司每天揽件数的数学期望;若你是公司决策者,根据公司每天所获利润的期望值,决定是否裁减前台工作人员人?
高二理科数学答案
1
2
3
4
5
6
7
8
9
10
11
12
A
B
B
C
C
B
D
C
B
B
A
C
13. -1 14. 15. 16.
17,
18(1).,(2)
21. (I)平面, (Ⅱ)(III)存在,为中点.
22.(1) (2) ①12 ②应裁减1人