2017-2018学年河南省南阳一中高二下学期第一次月考数学理试题（解析版） 11页

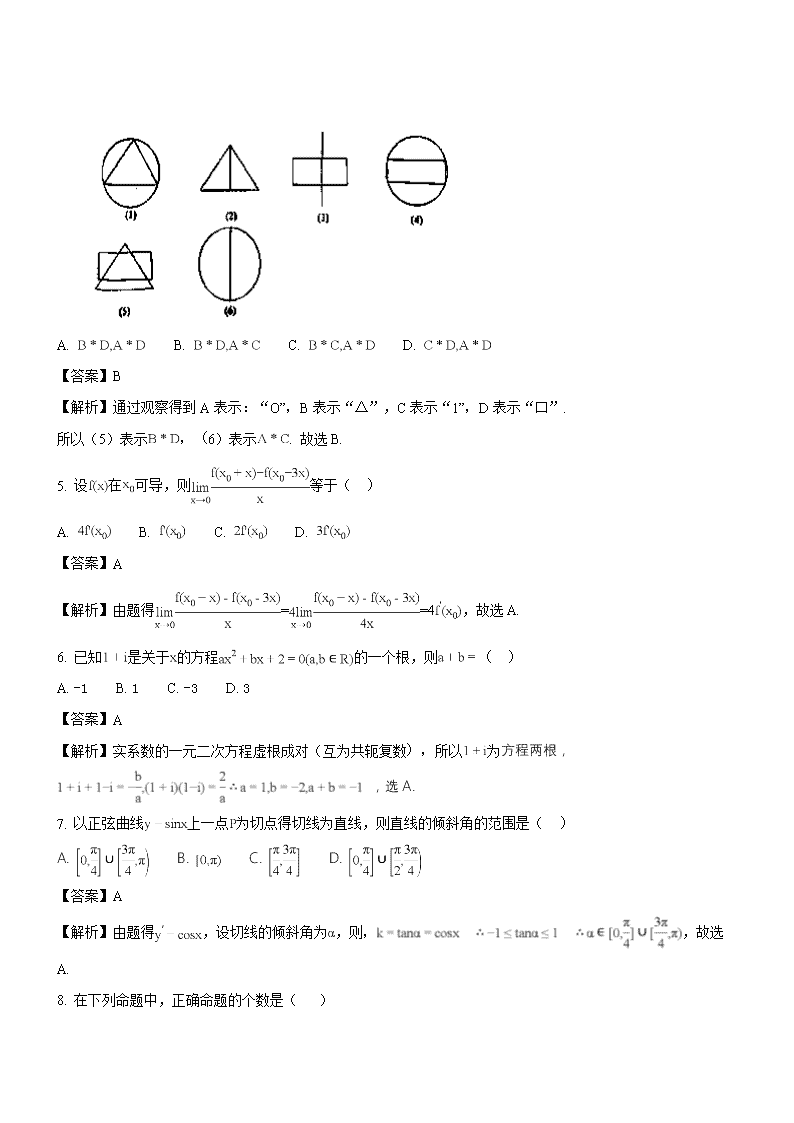
‎2017-2018学年河南省南阳一中高二下学期第一次月考数学理试题（解析版）‎ 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 已知是虚数单位，则复数=（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】因为复数===2+i．‎ 故选C．‎ ‎2. 设，那么等于（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】由题得 ‎,故选A.‎ ‎3. 曲线在点处的切线与坐标轴围成的三角形的面积为（ ）‎ A. 2 B. C. D. 1‎ ‎【答案】D ‎【解析】由题得,所以,‎ 所以切线方程为 当x=0时，y=2;当y=0时，x=1.‎ 所以切线与坐标轴围成的三角形的面积为，故选D.‎ ‎4. 定义的运算分别对应下面图中的（1），（2），（3），（4），则图中（5），（6）对应的运算是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】通过观察得到A表示：“O”，B表示“△”，C表示“1”，D表示“口”.‎ 所以（5）表示，（6）表示. 故选B.‎ ‎5. 设在可导，则等于（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】由题得==4，故选A.‎ ‎6. 已知是关于的方程的一个根，则（ ）‎ A. -1 B. 1 C. -3 D. 3‎ ‎【答案】A ‎【解析】实系数的一元二次方程虚根成对（互为共轭复数），所以为方程两根， ，选A.‎ ‎7. 以正弦曲线上一点为切点得切线为直线，则直线的倾斜角的范围是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】由题得，设切线的倾斜角为，则，，故选A.‎ ‎8. 在下列命题中，正确命题的个数是（ ）‎ ‎①两个复数不能比较大小；‎ ‎②复数对应的点在第四象限；‎ ‎③若是纯虚数，则实数；‎ ‎④若，则.‎ A. 0 B. 1 C. 2 D. 3‎ ‎【答案】A ‎【解析】对于选项①,不能说两个复数不能比较大小，如复数3和4就可比较大小，所以该命题是错误的.对于选项②，复数对应的点在第二象限，所以该命题是错误的.对于选项③，若是纯虚数，则=0且≠0，所以x=1,所以该命题是错误的. 对于选项④，若，可以，‎ 所以该命题是错误的. 故选A.‎ ‎9. 已知函数，则其导函数的图象大致是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】 ‎ ‎∴其导函数 为偶函数，图象关于轴对称，故排除A，B，‎ 当时，故排除D，故选：C．‎ 点睛：本题考查了导数的运算法则和函数图象的识别，属于基础题．‎ ‎10. “一支医疗救援队里的医生和护士，包括我在内，总共是13名.下面讲到的人员情况，无论是否把我计算在内，都不会有任何变化.在这些医务人员中：①护士不少于医生；②男医生多于女护士；③女护士多于男护士；④至少有一位女医生.”由此推测这位说话人的性别和职务是（ ）‎ A. 男护士 B. 女护士 C. 男医生 D. 女医生 ‎【答案】A ‎【解析】由题设可知：若说话人是女护士，则②的说法不正确，即答案B不真；若说话人是男医生，则③的说法不正确，即答案C 错误；若说话人是女医生，则①的说法不真，据此可推测该说话人应是男护士人，应选答案A。‎ 点睛：本题考查的是推理与证明中的推理和论证能力的问题。解答时要综合运用好题设中所提供的有关有效信息，逐一作出真假的判定。推理时有时从正面进行推断，有时也从反面进行推证，即推理的方式有直接证明与间接证明两条途径。‎ ‎11. 给出定义：设是函数的导函数，是函数的导函数，若方程有实数解，则称点为函数的“拐点”.已知函数的拐点是，则点（ ）‎ A. 在直线上 B. 在直线上 C. 在直线上 D. 在直线上 ‎【答案】A ‎【解析】由题得.‎ 所以，所以拐点在直线上.‎ 故选A.‎ ‎12. 若自然数使得作竖式加法均不产生进位现象，则称为“开心数”.例如：32是“开心数”.因32+33+34不产生进位现象；23不是“开心数”，因23+24+25产生进位现象，那么，小于100的“开心数”的个数为（ ）‎ A. 9 B. 10 C. 11 D. 12‎ ‎【答案】D ‎【解析】根据题意个位数需要满足要求：‎ ‎∵n+（n+1）+（n+2）＜10，即n＜2.3，‎ ‎∴个位数可取0，1，2三个数，‎ ‎∵十位数需要满足：3n＜10， ∴n＜3.3，‎ ‎∴十位可以取0，1，2，3四个数，故四个数的“开心数”共有3×4=12个．‎ 故选D．‎ 点睛：本题的关键是解题策略，本题可以列举，但是比较复杂，所以可以通过分析得到个位数和十位数的特征，从而得到开心数的个数，比较简洁.‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13. 复数（是虚数单位），则在复平面内对应的点位于第__________象限．‎ ‎【答案】二 ‎【解析】由题得，所以在复平面内对应的点位于第二象限，故填二.‎ ‎【答案】‎ ‎【解析】由题得.‎ 所以，故填.‎ ‎15. 我们知道，在边长为的正四面体内任一点到其四个面的距离之和为定值__________．‎ ‎【答案】‎ ‎【解析】如图：由棱长为a可以得到BF=a，‎ BO=AO=a，‎ 在直角三角形中，根据勾股定理可以得到BO2=BE2+OE2，‎ 把数据代入得到OE=a，‎ ‎∴棱长为a的三棱锥内任一点到各个面的距离之和4×a=a，‎ 故选A．‎ ‎16. 二维空间中圆的一维测量（周长），二维测量（面积），观察发现；三维空间中球的二维测度（表面积），三维测度（体积），观察发现.已知四维空间中“超球”的三维测度，猜想其四维测度=__________．‎ ‎【答案】‎ ‎【解析】二维空间中的圆的一维测度（周长），二维测度（面积），观察发现，三维空间中球的二维测度（表面积），三位测度（体积），观察发现，所以四维空间中“超球”的三维测度，猜想其四维测度，则，故填．‎ 点睛：本题考查的是不完全归纳法，涉及观察、归纳、猜想，属于难题．首先要学会观察题目给出的几个数据之间的关系，能够发现其关系就是前面的是后面的导数，只要发现并验证这个关系，就可以用其解决后面提出的问题，从而知．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. 求下列函数的导数.‎ ‎（1）； （2）； （3）.‎ ‎【答案】(1)；(2)；(3).‎ ‎【解析】试题分析：（1）第（1）问，直接利用商的导数的求导法则求解. (2)第（2）问直接利用和的导数求导. (3)直接利用复合函数的导数的求导法则解答.‎ 试题解析：‎ ‎（1）.‎ ‎（2）因为，‎ 所以.‎ ‎（3）函数看作和的复合复数，‎ 点睛：求导的关键是首先从总体上把握这个函数的结构，再去求导.如（3），函数就是两个复合函数的差，所以先求两个复合函数的导数，再求它们导数的差.‎ ‎18. 为何实数时，复数满足下列要求：‎ ‎（1）是纯虚数；‎ ‎（2）在复平面内对应的点在第二象限；‎ ‎（3）在复平面内对应的点在直线上.‎ ‎【答案】(1)；(2)；(3).‎ ‎【解析】试题分析：（1）先将复数化为的形式，再根据纯虚数的定义，即可求得实数的值；（2）把复数化为的形式后，再令即可求得实数的取值范围；（3）把复数 化为的形式后，再利用即可求得的值.‎ 试题解析：（1） ‎ ‎，得，即时，是纯虚数．‎ ‎（2）由，得，‎ 即时，在复平面内对应的点在第二象限.‎ ‎（3）由，得，‎ 即时，在复平面内对应的点在直线上.‎ 考点：1、纯虚数；2、复平面.‎ ‎19. 设函数且.‎ ‎（1）试用反证法证明：；‎ ‎（2）证明：.‎ ‎【答案】(1)证明见解析；(2)证明见解析.‎ ‎【解析】（1）首先假设，从而由结合推出矛盾，使问题得证；（2）根据条件判断出，，即可使问题得证．‎ 试题分析：‎ 试题解析：证明：（1）假设，‎ ‎∵，∴，‎ 将上述不等式相加得，‎ ‎∵，∴，‎ 这与矛盾，‎ ‎∴假设不成立，∴．‎ ‎（2）∵，∴，‎ ‎∴，∴．‎ ‎∵，∴．‎ ‎∵，∴．‎ 考点：1、反证法；2、综合法．‎ ‎【方法点睛】用反证法证明命题的一般步骤是第一步：假设命题的结论不成立，即假设结论的反面成立；第二步：从这个假设出发，经过推理论证，得出矛盾；第三步：由矛盾判定假设不正确，从而肯定命题的结论正确.‎ ‎20. 若存在过点的直线与曲线和都相切，求实数的值.‎ ‎【答案】或.‎ ‎【解析】试题分析：本题主要考查利用导数求函数的切线等基础知识，同时也考查学生分析问题解决问题的能力.先设直线与已知函数的切点，利用导数得切线斜率，既得切线方程，把点代入切线方程，可得切点坐标，从而得直线方程，又与相切，可得的值.‎ 试题解析：设过的直线与相切于点，所以切线方程为 即，又在切线上，则或，‎ 当时，由与相切可得，‎ 当时，由与相切可得.‎ 考点：利用导数求函数的切线方程.‎ ‎21. 设函数，曲线在点处的切线方程为.‎ ‎（1）求的解析式；‎ ‎（2）证明：曲线上任一点处的切线与直线和直线所围成的三角形面积为定值，并求此定值.‎ ‎【答案】(1)；(2)证明见解析.‎ ‎【解析】解：(1)方程7x－4y－12＝0可化为y＝x－3，‎ 当x＝2时，y＝．‎ 又f′(x)＝a＋，‎ 于是，解得 故f(x)＝x－．‎ ‎(2)证明：设P(x0，y0)为曲线上任一点，由f′(x)＝1＋知，曲线在点P(x0，y0)处的切线方程为y－y0＝(1＋)·(x－x0)，即y－(x0－)＝(1＋)(x－x0)．‎ 令x＝0得，y＝－，从而得切线与直线x＝0，交点坐标为(0，－)．‎ 令y＝x，得y＝x＝2x0，从而得切线与直线y＝x的交点坐标为(2x0,2x0)．‎ 所以点P(x0，y0)处的切线与直线x＝0，y＝x所围成的三角形面积为|－||2x0|＝6．‎ 曲线y＝f(x)上任一点处的切线与直线x＝0和直线y＝x所围成的三角形面积为定值，此定值为6．‎ 视频 ‎22. 已知数列的前项和（为正整数）.‎ ‎（1）令，求证数列是等差数列，并求数列的通项公式；‎ ‎（2）令，试比较与的大小，并予以证明.‎ ‎【答案】(1)证明见解析；(2)答案见解析.‎ ‎【解析】试题分析：（1）已知，一般利用进行化简条件，当时，，，又数列是首项和公差均为1的等差数列，于是.（2）由（1）得，是等差乘等比型，所以其和求法为“错位相减法”， 即得.数列中比较大小，一般用作差，即,而比较的大小，有两个思路，一是数学归纳法，二是二项展开式定理.‎ 试题解析：（1）在中，令n=1，可得，即1‎ 当时，， 2‎ ‎.‎ 又数列是首项和公差均为1的等差数列 4‎ 于是.6‎ ‎(2)由（1）得，所以 由①-②得 ‎9‎ ‎2‎ 于是确定的大小关系等价于比较的大小 猜想：当证明如下：‎ 证法1：（1）当n=3时，由猜想显然成立．‎ ‎（2）假设时猜想成立．即 则时，‎ 所以当时猜想也成立 综合（1）（2）可知 ，对一切的正整数，都有 证法2：当时 综上所述，当 ，当时14‎ 考点：等差数列定义，错位相减法求和，数学归纳法证明不等式