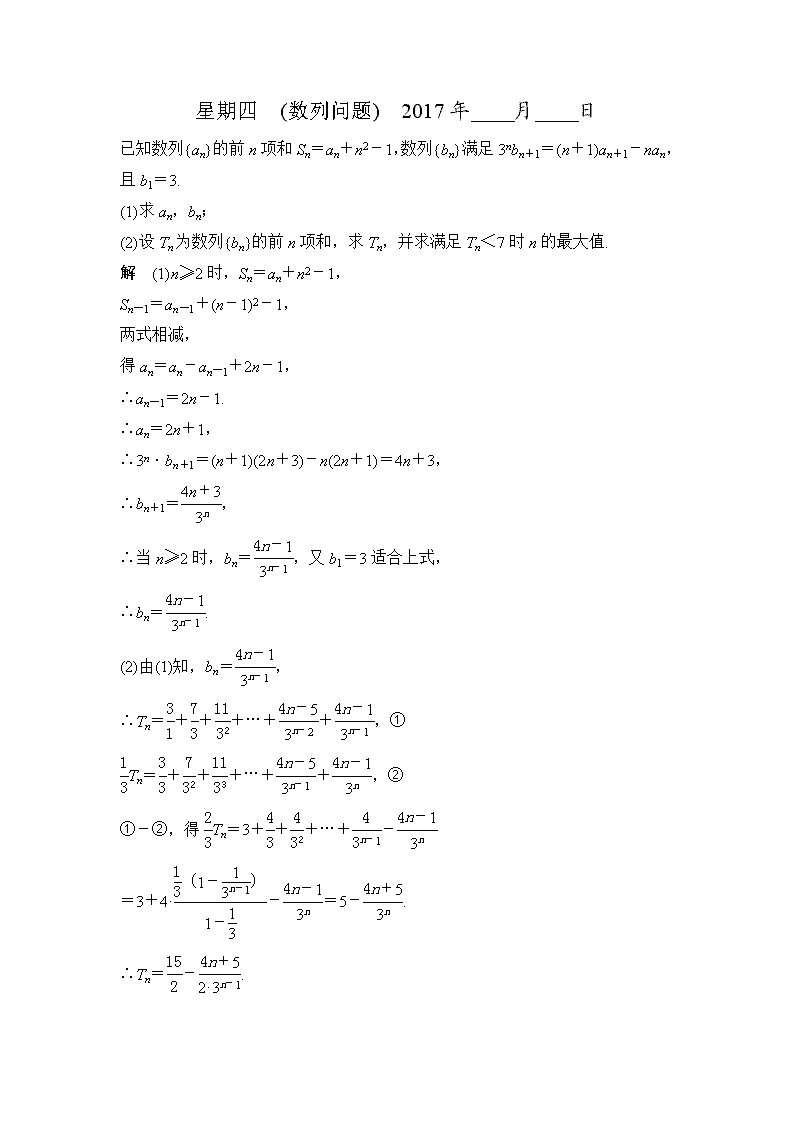2017届高考数学（文）二轮复习（江苏专用）解答题 第一周 星期四 2页

星期四　(数列问题)　2017年____月____日 已知数列{an}的前n项和Sn＝an＋n2－1，数列{bn}满足3nbn＋1＝(n＋1)an＋1－nan，且b1＝3.‎ ‎(1)求an，bn；‎ ‎(2)设Tn为数列{bn}的前n项和，求Tn，并求满足Tn＜7时n的最大值.‎ 解　(1)n≥2时，Sn＝an＋n2－1，‎ Sn－1＝an－1＋(n－1)2－1，‎ 两式相减，‎ 得an＝an－an－1＋2n－1，‎ ‎∴an－1＝2n－1.‎ ‎∴an＝2n＋1，‎ ‎∴3n·bn＋1＝(n＋1)(2n＋3)－n(2n＋1)＝4n＋3，‎ ‎∴bn＋1＝，‎ ‎∴当n≥2时，bn＝，又b1＝3适合上式，‎ ‎∴bn＝.‎ ‎(2)由(1)知，bn＝，‎ ‎∴Tn＝＋＋＋…＋＋，①‎ Tn＝＋＋＋…＋＋，②‎ ‎①－②，得Tn＝3＋＋＋…＋－ ‎＝3＋4·－＝5－.‎ ‎∴Tn＝－.‎ Tn－Tn＋1＝－＝＜0.‎ ‎∴Tn＜Tn＋1，即{Tn}为递增数列.‎ 又T3＝＜7，T4＝＞7，‎ ‎∴Tn＜7时，n的最大值为3.‎