- 605.50 KB
- 2021-06-20 发布
- 1、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 2、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报QQ:3215808601
青浦区2017-2018学年第一学期九年级期终学业质量调研测试
数学试卷 2018.1
(完成时间:100分钟 满分:150分 )
考生注意:
1.本试卷含三个大题,共25题,答题时,考生务必按答题要求在答题纸规定的位置作答,在草稿纸上,本试卷上答题一律无效。
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤。
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】
1. 计算的结果是( )
(A); (B); (C); (D).
2. 如果一次函数的图像经过一、二、三象限,那么、应满足的条件是( )
(A),且; (B),且;
(C),且; (D),且.
3. 下列各式中,的有理化因式是( )
(A); (B); (C); (D).
图1
4.如图1,在中,,是边上的高.如果,,那么
是( )
(A); (B);
(C); (D).
图2
5. 如图2,在中,点在边上,射线、交于点,下列等式成立的是( )
(A); (B);
(C); (D).
6. 在梯形中,,下列条件中,不能判断梯形ABCD是等腰梯形的是( )
(A); (B); (C); (D).
二、填空题:(本大题共12题,每题4分,满分48分)
7.因式分解: .
8. 函数的定义域是 .
9. 如果关于的一元二次方程没有实数根,那么的取值范围是 .
10. 抛物线的对称轴是 .
11. 将抛物线平移,使它的顶点移到点,平移后新抛物线的表达式为 .
12. 如果两个相似三角形周长的比是,那么它们面积的比是 .
13. 如图3,传送带和地面所成斜坡的坡度为,把物体从地面处送到坡顶处时,物体所经过的路程是12米,此时物体离地面的高度是 米.
14. 如图4,在中,点是边的中点.如果,,那么 (结果用含、的式子表示).
15. 已知点、分别在的边、的延长线上,且,如果,,那么= .
16. 在中,,,点为的重心.如果,那么的值是 .
17. 将一个三角形经过放大后得到另一个三角形,如果所得三角形在原三角形的外部,这两个三角形各对应边平行且距离都相等,那么我们把这样的两个三角形叫做“等距三角形”,它们对应边之间的距离叫做“等距”.如果两个等边三角形是“等距三角形”,它们的“等距”是1,那么它们周长的差是 .
图3
图4
图5
18. 如图5,在中,,,,点、分别在边、上,将沿着所在直线翻折,点落在点处,、分别交边于点、,如果,,垂足为点,那么的长是 .
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
计算: .
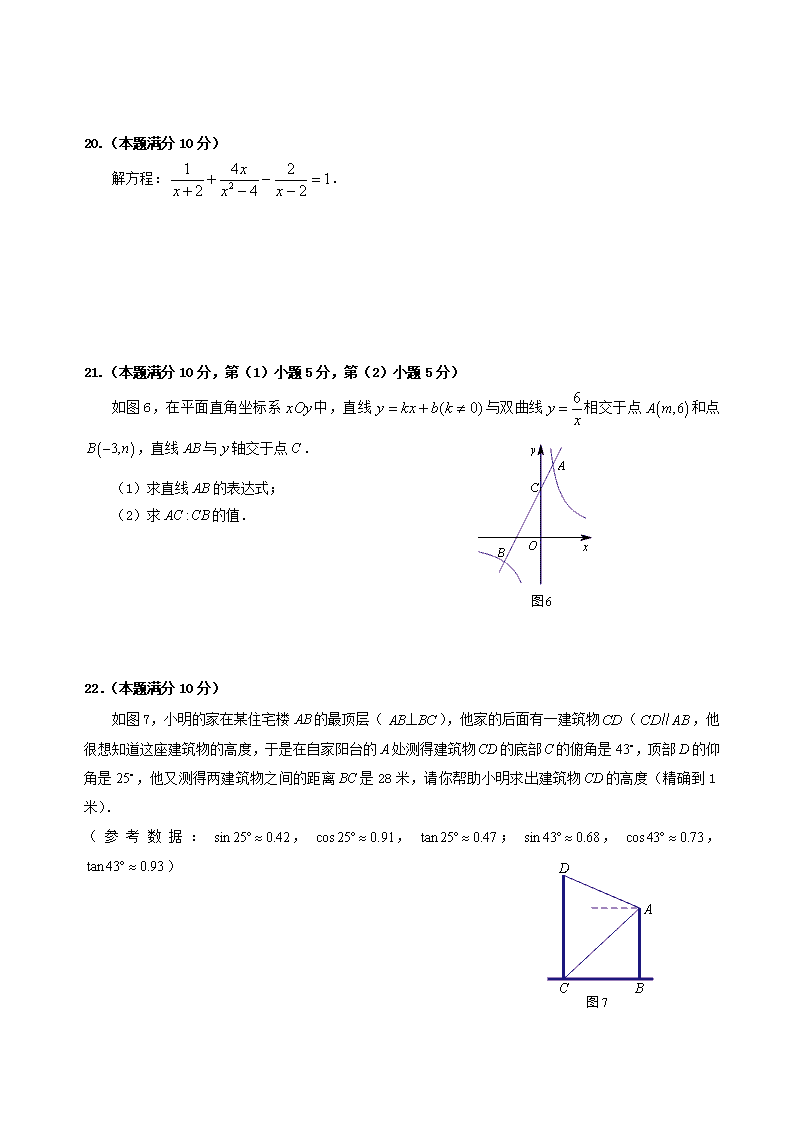
20.(本题满分10分)
解方程:.
21.(本题满分10分,第(1)小题5分,第(2)小题5分)
图6
如图6,在平面直角坐标系中,直线与双曲线相交于点和点,直线与轴交于点.
(1)求直线的表达式;
(2)求的值.
22.(本题满分10分)
如图7,小明的家在某住宅楼的最顶层(),他家的后面有一建筑物(,他很想知道这座建筑物的高度,于是在自家阳台的处测得建筑物的底部的俯角是,顶部的仰角是,他又测得两建筑物之间的距离是28米,请你帮助小明求出建筑物的高度(精确到1米).
图7
(参考数据:,,;,,)
23.(本题满分12分,第(1)小题4分,第(2)小题8分)
图8
如图8,已知点、分别在的边、上,线段与交于点,且.
(1)求证:;
(2)若,求证:.
24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分)
如图9,在平面直角坐标系中,抛物线与轴相交于点和点,与轴交于点,对称轴为直线.
(1)求点的坐标(用含的代数式表示);
(2)联结、,若的面积为6,求此抛物线的表达式;
(3)在第(2)小题的条件下,点为轴正半轴上一点,点与点,点与点关于点成中心对称,当为直角三角形时,求点的坐标.
图9
25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)
如图10,在边长为2的正方形中,点是边上的动点(点不与点、点重合),点是边上一点,联结、,且.
(1)当时,求的正切值;
(2)设,,求关于的函数解析式;
(3)联结,在中是否存在度数不变的角,若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
图10
备用图
您可能关注的文档
相关文档
- 湖北省黄陂六中2018-2019学年高二2021-06-20 03:23:356页
- 2019山东省威海中考数学试卷解析版2021-06-20 03:22:2320页
- 期中考试后的家长会教师发言稿2021-06-20 03:21:185页
- 2018年江苏省泰州市中考物理试题(解2021-06-20 03:21:0822页
- 体育计划总结之初三体育中考教学反2021-06-20 03:20:192页
- 辽宁省沈阳市城郊市重点联合体20202021-06-20 03:20:0618页
- 2018-2019学年江西省铅山县一中高2021-06-20 03:19:195页
- 2018-2019学年山东省济南第一中学2021-06-20 03:19:0711页
- 【生物】江苏省马坝高级中学2019-22021-06-20 03:15:188页
- 内蒙古包钢一中2019-2020学年高二2021-06-20 03:15:068页