北师大版数学九年级 上册 第四章 4 5页

北师大版九年级 上册 第四章 图形的相似 ‎4.6利用相似三角形测高 同步练习 ‎1.相似三角形对应　　　　的比,对应　　　　的比,对应　　　　的比都等于相似比.‎ ‎2.如果两个相似三角形对应高的比为4：5,那么这两个相似三角形的相似比为　　　　,对应中线的比为　　　　　,对应角平分线的比为　　　　.‎ ‎3.已知△ABC∽△DEF,△ABC的周长为4,△DEF的周长为2,则△ABC与△DEF的面积之比为　　　　.‎ ‎4.顺次连接三角形三边的中点,所形成的三角形与原三角形对应高的比是(　　)‎ A.1：4‎ B.1：3‎ C.1：‎ D.1：2‎ ‎5.两个三角形的面积之比为5,周长之比为m,则为(　　)‎ A.1‎ B.‎ C.‎ D.5‎ ‎6.△ABC∽△A1B1C1,AB=4,A1B1=12,则它们对应边上的高的比是　　　　,若BC边上的中线为1.5,则B1C1上的中线A1D1=　　　　.‎ ‎7.两个三角形的相似比为1：3,较大的三角形一角的平分线长12 cm,则较小三角形的对应角的平分线长为　　　　cm.‎ ‎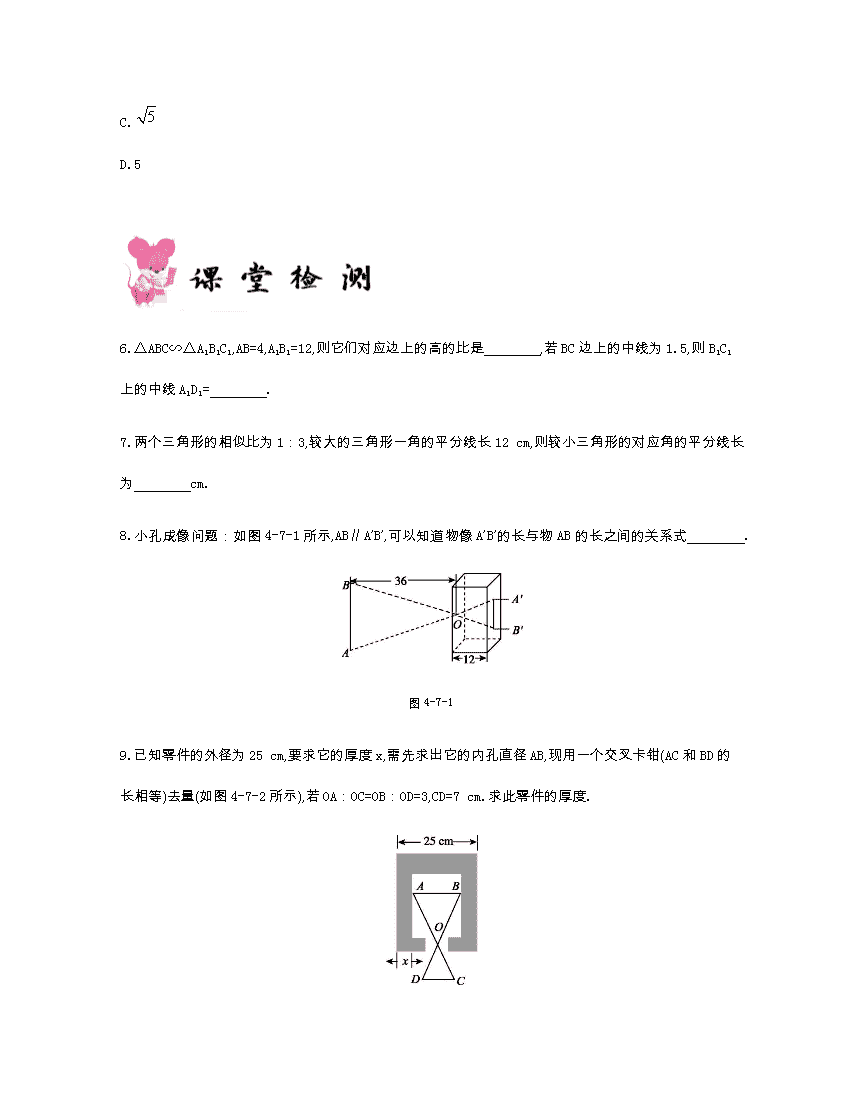8.小孔成像问题：如图4-7-1所示,AB∥A’B’,可以知道物像A’B’的长与物AB的长之间的关系式　　　　.‎ 图4-7-1‎ ‎9.已知零件的外径为25 cm,要求它的厚度x,需先求出它的内孔直径AB,现用一个交叉卡钳(AC和BD的长相等)去量(如图4-7-2所示),若OA：OC=OB：OD=3,CD=7 cm.求此零件的厚度.‎ 图4-7-2‎ ‎10.若两个相似三角形的对应角的角平分线的比为3：5,则它们的相似比为(　　)‎ A.1：3‎ B.3：5‎ C.1：5‎ D.9：25‎ ‎11.把一个三角形改作成和它相似的三角形,如果一条边上的高缩小到原来的,那么各边长都应缩小到原来的　　　　.‎ ‎12.已知△ABC∽△A’B’C’,且BC：B’C’=3：2,△ABC的周长为24,则△A’B’C’的周长为　　　　.‎ ‎13.已知点A,B,C,D的坐标如图4-7-3所示,E是图中两条虚线的交点,若△ABC∽△ADE,则点E的坐标是　　　　.‎ 图4-7-3‎ ‎14.一条河的两岸有一段是平行的,在河的南岸每相距5 m栽一棵树,在河的北岸每相距50 m立一根电线杆.在南岸离开岸边25 m处看北岸,看到北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.‎ 图4-7-4‎ 参考答案 ‎1.高　　　角平分线　　　中线 ‎2.4：5　　　4：5　　　4：5‎ ‎3.4：1‎ ‎4.D ‎5.C ‎6.1：3　　　4.5‎ ‎7.4‎ ‎8.A’B’=AB ‎9.解：∵==3,∠AOB=∠COD,‎ ‎∴△AOB∽△COD,∴==3,‎ ‎∴AB=21 cm,‎ ‎∴2x=25-21,∴x=2 cm.‎ ‎10.B ‎11.‎ ‎12.16‎ ‎13.(4,-3)‎ ‎14.解：设河宽为x m,由相似三角形的性质得 ‎=,‎ 解得x=37.5.‎ 答：河宽为37.5 m. ‎