- 2.65 MB
- 2024-05-06 发布
集宁一中西校区高一年级2019—2020学年
第一学期期末考试 数学文科试题
本试卷满分为150分,考试时间为120分钟。
第I卷(选择题 共60分)
一、 选择题:(本大题共12小题,每小题5分,共60分。)
1.设全集,集合,则 ( )
A. B. C. D.
2.下列函数中,与函数相等的是( )
A. B. C. D.
3.若直线和没有公共点,则与的位置关系是( )
A.相交 B.平行 C.异面 D.平行或异面
4.若函数,则的值为( )
A.0 B.2 C.4 D.6
5.在同一直角坐标系中,函数, (,且)的图象大致为( )
A. B.C.D.
6.已知函数y=f(x)+x是偶函数,且f(2)=1,则f(-2)=( )
A.2 B.3 C.4 D.5
7.已知函数在区间上既没有最大值也没有最小值,则实数的取值范围是( )
A. B. C. D.
8.已知m,n表示两条不同直线,表示平面.下列说法正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
9.若,则的值为 ( )
A.3 B. C.6 D.
10. 函数的零点所在的一个区间是( )
A. B. C. D.
11. 用长为、宽为的矩形做侧面,围成一个高为的圆柱,此圆柱的轴截面面积为( )
A. B. C. D.
12.设奇函数在上为增函数,且,则不等式的解集为( )
A. B.
C. D.
第Ⅱ卷(非选择题 共90分)
二、 填空题:(本大题共4个小题,每小题5分,共20分。)
13.已知幂函数的图像过点,则 ;
14.已知长方体的长、宽、高分别为,则该长方体的外接球的表面积为__________;
15.函数在区间上的值域为 ;
16.函数有两个零点,则的取值范围 。
三、解答题(本大题共6小题,17题10分,18---22每题12分,共70分)
17.已知集合,.
(1)求
(2)求.
18.计算下列各式的值.
(1)
(2)
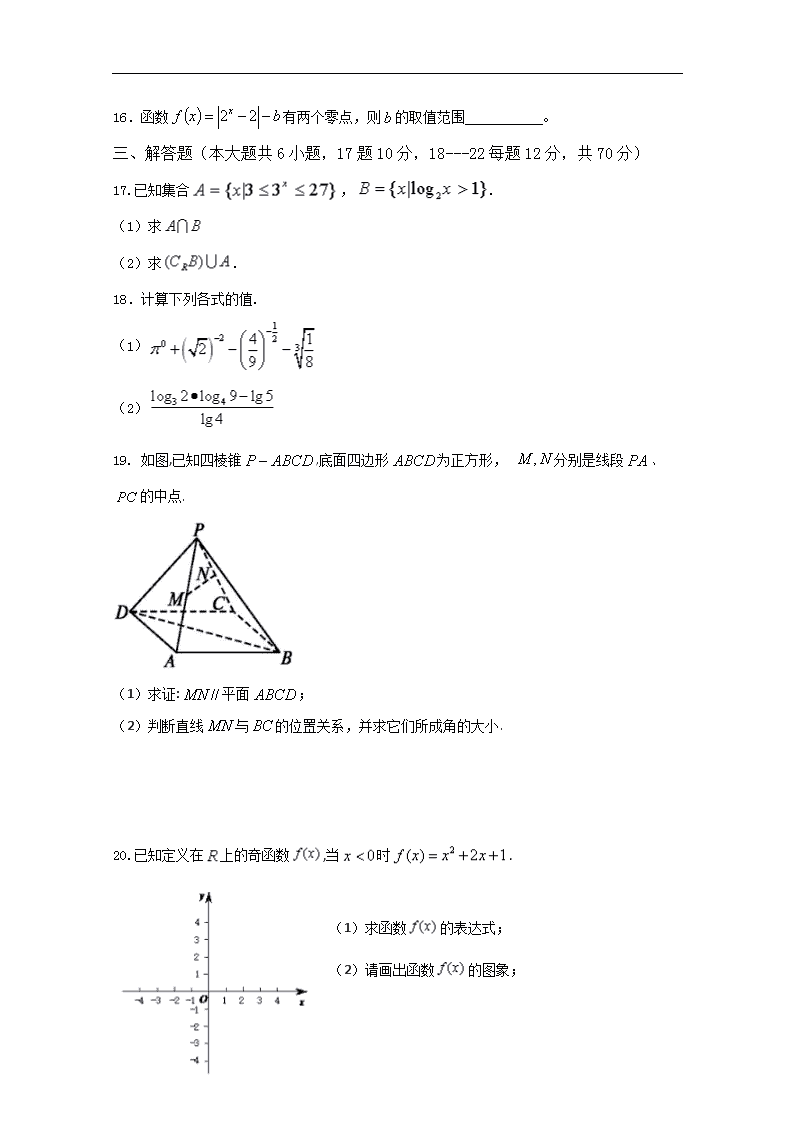
19. 如图,已知四棱锥,底面四边形为正方形, 分别是线段、的中点.
(1)求证:平面;
(2)判断直线与的位置关系,并求它们所成角的大小.
20.已知定义在上的奇函数,当时.
(1)求函数的表达式;
(2)请画出函数的图象;
(3)写出函数的单调区间.
21.如图,四棱锥中,平面,底面是正方形,且,为中点.
(1)求证:平面;
(2)求点到平面的距离.
22. 已知函数,其中且.
(1)求函数的定义域;
(2)判断的奇偶性并予以证明;
(3)若,求的取值范围.
2019-2020高一期末考试文科数学答
1-12 CADDAD CBCBBD
13. 14. 15. 16.
17. (1)<;(2)
【详解】
(1)由得,故;
由>得>,故>
∴<
(2)由>得
∴
【点睛】
本题考查指数不等式、对数不等式以及集合交并补运算,考查基本求解能力,属基础题.
18. (1);(2).
【解析】(1)
(2)
19.(1)见解析;(2)
【详解】(1)连接,在三角形中,分别是的中点,所以是三角形的中位线,所以,由于平面,平面,所以平面.
(2)由于,与相交,所以与为异面直线,且是异面直线与所成角,由于四边形是正方形,所以.
20. (1);(2)见解析;(3)递增区间是;递减区间是
【解析】(1)设
又是定义在上的奇函数,
所以
当时,
所以
(2)图象:
(3)递增区间是;递减区间是
【点睛】本题考查函数的图象以及函数的单调性的判断,函数的解析式的求法,考查计算能力.
21.(1)证明:平面,
又正方形中,
平面·
又平面,,
,是的中点,
∴,
平面·
(2)过点作于点,由(1)知平面平面,
又平面平面,平面,
线段的长度就是点到平面的距离·
,
,
·
∴点到平面的距离为.
【点睛】本题主要考查线面垂直的判定和性质,考查点到平面的距离,属于基础题.
22.【详解】
(1)根据题意,,
所以 ,解得:
故函数的定义域为:
(2)函数为奇函数。
证明:由(1)知的定义域为,关于原点对称,
又,故函数为奇函数。
(3)根据题意,
当 , 可得,
则,解得:
当, 可得,
则,解得
综上可得,当0<a<1时,﹣1<x<0;当a>1时,0<x<1.
【点睛】
本题主要考查函数的奇偶性以及对数函数的相关知识,掌握对数函数真数大于零以及对数函数的单调性,学会解不等式组。