- 760.00 KB
- 2024-04-11 发布
合肥九中2018 - 2019学年第一学期高二第一次月考
数学试卷
(考试时间120分钟 满分150分)
第Ⅰ卷(选择题)
一.选择题:(共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项.)
1.将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括( )
A.一个圆台、两个圆锥 B.两个圆台、一个圆柱
C.两个圆台、一个圆锥 D.一个圆柱、两个圆锥
2.圆锥的高扩大到原来的4倍,底面半径缩短到原来的,则圆锥的体积( )
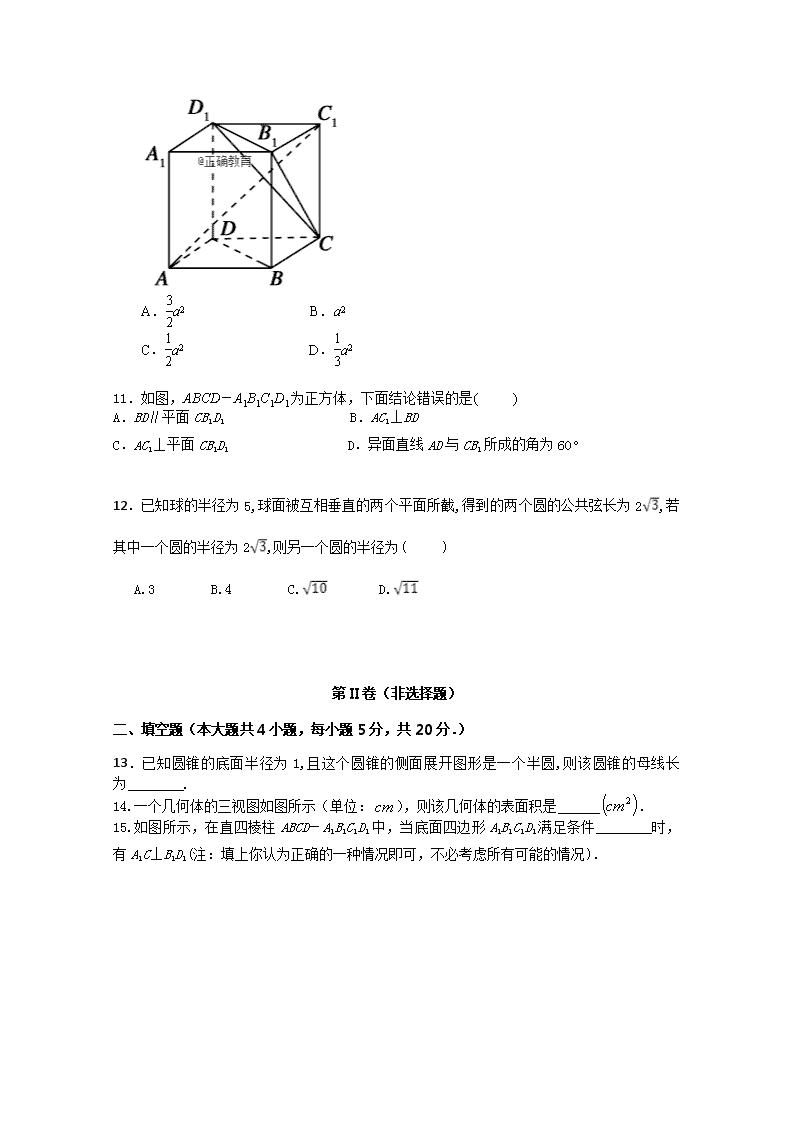
A.缩小到原来的一半 B.扩大到原来的2倍
C.不变 D.缩小到原来的
3. 下列命题正确的有( )
①若△ABC在平面α外,它的三条边所在直线分别交α于P,Q,R,则P,Q,R三点共线;②若三条平行线a,b,c都与直线l相交,则这四条直线共面;③三条直线两两相交,则这三条直线共面.
A.0个 B.1个
C.2个 D.3个
4.一个水平放置的平面图形的斜二测直观图是一个底角为,腰和上底均为1的等腰梯形,则这个平面图形的面积为( )
A. B. C. D.
5. 如图所示,在正方体ABCD—A1B1C1D1中,M、N分别是BB1、BC的中点.则图中阴影部分在平面ADD1A1上的正投影为( )
6.设是两条不同的直线,是三个不同的平面,给出下列四个命题:①若,则;②若,则;③若,则;④若,则.
其中正确命题的序号是: ( )
A、①② B、②③ C、③④ D、①④
7. 长方体的三个相邻面的面积分别为2,3,6,这个长方体的顶点都在同一个球面上,则这个球面的表面积为( )
A. B.56π C.14π D.64π
8.一正方体表面沿着几条棱裁开放平得到如图所示的展开图,则在原正方体中( )
A.AB∥CD B.AB∥平面CD
C.CD∥GH D.AB∥GH
9、圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )
A.7 B.6 C.5 D.3
10.如图所示,正四棱锥S—ABCD的所有棱长都等于a,过不相邻的两条棱SA,SC作截面SAC,则截面的面积为( )
A.a2 B.a2
C.a2 D.a2
11.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
A.BD∥平面CB1D1 B.AC1⊥BD
C.AC1⊥平面CB1D1 D.异面直线AD与CB1所成的角为60°
12.已知球的半径为5,球面被互相垂直的两个平面所截,得到的两个圆的公共弦长为2,若其中一个圆的半径为2,则另一个圆的半径为( )
A.3 B.4 C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,每小题5分,共20分.)
13.已知圆锥的底面半径为1,且这个圆锥的侧面展开图形是一个半圆,则该圆锥的母线长为 .
14.一个几何体的三视图如图所示(单位:),则该几何体的表面积是 .
15.如图所示,在直四棱柱ABCD-A1B1C1D1中,当底面四边形A1B1C1D1满足条件________时,有A1C⊥B1D1(注:填上你认为正确的一种情况即可,不必考虑所有可能的情况).
16.如图,正方体的棱长为1,P为BC的中点,Q为线段上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列结论正确的是________(写出所有正确结论的编号).
①当时,S为四边形
②当时,S为等腰梯形
③当时,S与的交点R满足
④当时,S为六边形
⑤当时,S的面积为
三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)如图,已知点E,F,G,H分别为正方体ABCD-A1B1C1D1的棱AB,BC,CC1,C1D1的中点,求证:EF,HG,DC三线共点.
18.(本题满分12分)已知正方体,是底对角线的交点.求证:
(1);(2).
19.(本题满分12分)如图,在四棱锥中,
底面
是的中点.
证明(1);(2)证明面平面;
20.(本题满分12分)已知正方体ABCD—A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=a,如图.
(1)求证:MN∥面BB1C1C;
(2)求MN的长.
21.(本题满分12分)如图1,在边长为1的等边三角形中,分别是上的点,,是的中点,与交于点,沿折起,得到如图2所示的三棱锥,其中.
(1)求证:;
(2)若为上的中点,为中点,求异面直线与所成角的余弦值
22. (本题满分12分)如图,四棱锥中,底面是以为中心的菱形,,,,为上一点,且.
(1)证明:;
(2)若,求四棱锥的体积.
合肥九中2018 - 2019学年第一学期高二第一次月考
数学试卷
(考试时间120分钟 满分150分) 命题人:周福远
第Ⅰ卷(选择题)
一.选择题:(共12小题,每小题5分,共60分。在每个小题给出的四个选项中,只有一项是符合题目要求的一项.)
1.将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括( D )
A.一个圆台、两个圆锥 B.两个圆台、一个圆柱
C.两个圆台、一个圆锥 D.一个圆柱、两个圆锥
2. 圆锥的高扩大到原来的4倍,底面半径缩短到原来的,则圆锥的体积( C )
A.缩小到原来的一半 B.扩大到原来的2倍
C.不变 D.缩小到原来的
3. 下列命题正确的有( C )
①若△ABC在平面α外,它的三条边所在直线分别交α于P,Q,R,则P,Q,R三点共线;②若三条平行线a,b,c都与直线l相交,则这四条直线共面;③三条直线两两相交,则这三条直线共面.
A.0个 B.1个
C.2个 D.3个
4.一个水平放置的平面图形的斜二测直观图是一个底角为,腰和上底均为1的等腰梯形,则这个平面图形的面积为(D )
A. B. C. D.
5. 如图所示,在正方体ABCD—A1B1C1D1中,M、N分别是BB1、BC的中点.则图中阴影部分在平面ADD1A1上的正投影为( A )
6.设是两条不同的直线,是三个不同的平面,给出下列四个命题:①若,则;②若,则;③若,则;④若,则.
其中正确命题的序号是: ( A )
A、①② B、②③ C、③④ D、①④
7. 长方体的三个相邻面的面积分别为2,3,6,这个长方体的顶点都在同一个球面上,则这个球面的表面积为( C )
A. B.56π C.14π D.64π
8.一正方体表面沿着几条棱裁开放平得到如图所示的展开图,则在原正方体中( C )
A.AB∥CD B.AB∥平面CD
C.CD∥GH D.AB∥GH
9、圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为(A )
A.7 B.6 C.5 D.3
10.如图所示,正四棱锥S—ABCD的所有棱长都等于a,过不相邻的两条棱SA,SC作截面SAC,则截面的面积为( C )
A.a2 B.a2
11.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( D )
A.BD∥平面CB1D1
B.AC1⊥BD
C.AC1⊥平面CB1D1
D.异面直线AD与CB1所成的角为60°
12.已知球的半径为5,球面被互相垂直的两个平面所截,得到的两个圆的公共弦长为2,若其中一个圆的半径为2,则另一个圆的半径为( B )
(A)3 (B)4 (C) (D)
解析:
如图设两圆的圆心分别为O1、O2,球心为O,公共弦为AB,其中点为E,
则OO1EO2为矩形,
AE=AB=,O1A=2,
所以O1E==3,
所以AO2==4,选B.
第II卷(非选择题)
二、填空题(本大题共4小题,每小题5分,共20分.)
13.已知圆锥的底面半径为1,且这个圆锥的侧面展开图形是一个半圆,则该圆锥的母线长为 .
解析:设母线长为x,根据题意得2πx÷2=2π×1,
解得x=2.
答案:2
14、一个几何体的三视图如图所示(单位:),则该几何体的表面积是 .
15.
如图所示,在直四棱柱ABCD-A1B1C1D1中,当底面四边形A1B1C1D1满足条件________时,有A1C⊥B1D1(注:填上你认为正确的一种情况即可,不必考虑所有可能的情况).
解析:由直四棱柱可知CC1⊥平面A1B1C1D1,所以CC1⊥B1D1,要使得B1D1⊥A1C,只要B1D1⊥平面A1CC1,所以只要B1D1⊥A1C1.此题还可以填写四边形A1B1C1D1是菱形、正方形等条件.
答案:B1D1⊥A1C1
16.如图,正方体的棱长为1,P为BC的中点,Q为线段上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是___①②③⑤______(写出所有正确命题的编号)。
①当时,S为四边形
②当时,S为等腰梯形
③当时,S与的交点R满足
④当时,S为六边形
⑤当时,S的面积为
三、解答题(本大题共6个大题,17-18每题10分,19-22每题12分,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)如图,已知点E,F,G,H分别为正方体ABCD-A1B1C1D1的棱AB,BC,CC1,C1D1的中点,求证:EF,HG,DC三线共点.
证明 ∵点E,F,G,H分别为所在棱的中点,连接BC1,GF,如图.
∴GF是△BCC1的中位线,∴GF∥BC1.
∵BE∥C1H,且BE=C1H,
∴四边形EBC1H是平行四边形.
∴EH∥BC1,∴GF∥EH.
∴E,F,G,H四点共面.
∵GF≠EH,故EF与HG必相交.
设EF∩HG=I.
∵I∈GH,GH⊂平面CC1D1D,
∴I∈平面CC1D1D.
同理可证I∈平面ABCD.
∴点I在交线DC上.即EF,HG,DC三线共点.
18、已知正方体ABCD﹣A1B1C1D1,O是底ABCD对角线的交点.求证:
(1)C1O∥面AB1D1;
(2)面OC1D∥面AB1D1.
解:(1)由题意:几何体ABCD﹣A1B1C1D1是正方体,O是底ABCD对角线的交点,
∴B1D1∥BD,
连接A1C1交于O1,连接AO1,
C1O1
∴C1O1AO是平行四边形.
∴AO1∥C1O.
∵AO1⊂面AB1D1;
∴C1O∥面AB1D1;
得证.
(2).∵B1D1∥BD,即OD∥B1D1,
OD⊂面OC1D,
∴OD∥面AB1D1.
由(1)可得C1O∥面AB1D1;
OD∩C1O=O,
所以:面OC1D∥面AB1D1.
19.(本题满分12分)如图,在四棱锥中,
底面
是的中点.
证明;(2)证明面平面;
解析:(1)证明:∵PA⊥底面ABCD,CD平面ABCD
∴PA⊥CD又AC⊥CD,ACPA=A
∴CD⊥平面PAC,又AE平面PAC
∴CD⊥AE
(2)证明:∵PA⊥底面ABCD,AB平面ABCD
∴PA⊥AB又AD⊥AB,ADPA=A
∴AB⊥平面PAD,又PD平面PAD
∴AB⊥PD由PA=AB=BC,∠ABC=60o则△ABC是正三角形
∴AC=AB∴PA=AC
∵E是PC中点∴AE⊥PC由(1)知AE⊥CD,又CDPC=C
∴AE⊥平面PCD∴AE⊥PD又AB⊥PD,ABAE=A
∴PD⊥平面ABE
从而面平面
20. (本题满分12分)已知正方体ABCD—A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=a,如图.
(1)求证:MN∥面BB1C1C;
(2)求MN的长.
解 (1)证明:作NP⊥AB于P,连接MP.NP∥BC,
∴==,
∴MP∥AA1∥BB1,
∴面MPN∥面BB1C1C.
MN⊂面MPN,
∴MN∥面BB1C1C.
(2)===,NP=a,
同理MP=a.
又MP∥BB1,
∴MP⊥面ABCD,MP⊥PN.
在Rt△MPN中MN==a.
21、如图1,在边长为1的等边三角形中,分别是,上的点,,是的中点,与交于点,沿折起,得到如图2所示的三棱锥,其中.
(1)求证:平面平面
(2)若为,上的中点,为中点,求异面直线与所成角的余弦值
证明:(1)如题图1,在等边三角形中,,
如题图2,平面,
平面 ··········2分
同理可证平面
,
平面平面
平面 ·········4分
(2)连
是的中位线
异面直线与所成角即为·····6分
,
又· ······8
22、如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=,M为BC上一点,且BM=.
(1)证明:BC⊥平面POM;
(2)若MP⊥AP,求四棱锥PABMO的体积.
解:(1)证明:如图,因四边形ABCD为菱形,O为菱形中心,连接OB,AM,则AO⊥OB.因∠BAD=,
故OB=AB·sin∠OAB=2sin=1,
又因BM=,且∠OBM=,在△OBM中,
OM2=OB2+BM2-2OB·BM·cos∠OBM
=12+2-2×1××cos=.
所以OB2=OM2+BM2,故OM⊥BM.
又PO⊥底面ABCD,所以PO⊥BC.从而BC与平面POM内两条相交直线OM,OP都垂直,
所以BC⊥平面POM.
(2)由(1)可得,OA=AB·cos∠OAB=2×cos=.
设PO=a,由PO⊥底面ABCD知,△POA为直角三角形,故PA2=PO2+OA2=a2+3.
由△POM也是直角三角形,故PM2=PO2+OM2=a2+.
在△ABM中,
AM2=AB2+BM2-2AB·BM·cos∠ABM=
22+2-2×2××cos=.
由已知MP⊥AP,故△APM为直角三角形,则
PA2+PM2=AM 2,即a2+3+a2+=,得a=,a=-(舍去),即PO=.
此时S四边形ABMO=S△AOB+S△OMB=·AO·OB+·BM·OM=××1+××=.
所以四棱锥P-ABMO的体积
VP-ABMO=·S四边形ABMO·PO=××=.