四川省成都外国语学校2019届高三开学考试数学（理）试卷 9页

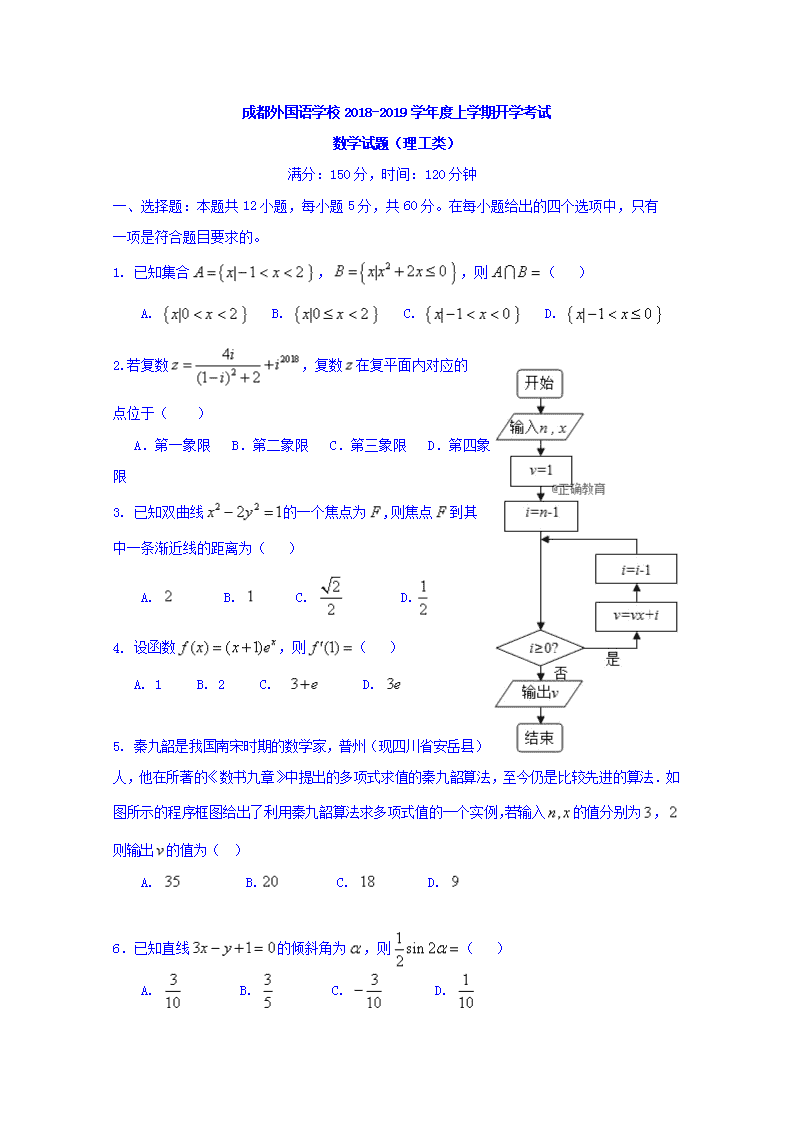
成都外国语学校 2018-2019 学年度上学期开学考试 数学试题（理工类） 满分：150 分，时间：120 分钟 一、选择题：本题共 12 小题，每小题 5 分，共 60 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。 1. 已知集合 ， ，则 （ ） A. B. C. D. 2.若复数 ，复数 在复平面内对应的 点位于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象 限 3. 已知双曲线 的一个焦点为 ,则焦点 到其 中一条渐近线的距离为（ ） A. B. C. D. 4. 设函数 ，则 （ ） A. 1 B. 2 C. D. 5. 秦九韶是我国南宋时期的数学家，普州（现四川省安岳县） 人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如 图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例，若输入 的值分别为 ， 则输出 的值为（ ） A. B. C. D. 6．已知直线 的倾斜角为 ，则 （ ） A. B. C. D. { }| 1 2 A x x= − < < { }2| 2 0 B x x x= + ≤ A B = { }|0 2 x x< < { }|0 2 x x≤ < { }| 1 0 x x− < < { }| 1 0 x x− < ≤ 2018 2 4 (1 ) 2 iz ii = +− + z 2 22 1x y− = F F 2 1 2 2 1 2 ( ) ( 1) xf x x e= + (1)f ′ = 3 e+ 3e xn, 3 2 v 35 20 18 9 3 1 0x y− + = α 1 sin 22 α = 3 10 3 5 3 10 − 1 10 7. 已知二项式 的展开式中 的系数为 ，则 的值为（ ） A． B． C. D． 8．设 ， ， ，则（ ） A. B. C. D. 9. 定 义 域 为 的 奇 函 数 的 图 像 关 于 直 线 对 称 ， 且 ， 则 （ ） A. 2018 B. 2020 C. 4034 D. 2 10.已知三棱锥 四个顶点均在半径为 的球面上，且 ，若 该三棱锥体积的最大值为 1，则这个球的表面积为（ ） A. B. C. D. 11.已知椭圆 的左、右焦点分別为 ，过 的直线与椭圆交于 两点，若 是以 为直角项点的等腰直角三角形，则椭圆的离心率为（ ） A． B． C. D． 12. 已知函数 ，若函数 与 有相同的值域，则 的取值范围是（ ） A． B． C． D． 二、填空题：本题共 4 小题，每小题 5 分，共 20 分。 13.计算 ___________. 91( )2x ax + 3x 21 2 − ( )1 e ax dxx +∫ 2 1 2 e + 2 3 2 e − 2 3 2 e + 2 5 2 e − 5sin π=a 3log 2 =b 3 2 4 1     =c bca << cab << bac << abc << R ( )y f x= 2x = (2) 2018f = (2018) (2016)f f+ = ABCD − R 22 === ACBCAB ， 81 500π π4 9 25π 9 100π 2 2 2 2 1( 0)x y a ba b + = > > 1 2,F F 2F ,A B 1F AB∆ A 2 2 2 3− 5 2− 6 3− ( ) ln 2f x x x x a= − + ( )y f x= ( ( ))y f f x= a 1( ,1]2 ( ,1]−∞ 3[1, )2 [1, )+∞ 2 3 2 3 1(log 9) (log 2) ( )8 ⋅ ⋅ = 14. 已知 满足 ，则 的最大值为__________． 15. 当函数 ， 取得最小值时， ________. 16.已知平面向量 满足 ，且 与 的夹角为 150°，则 的取值 范围是____________ . 三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17—21 题为必考题， 每个试题考生都必须作答。第 22、 23 题为选考题，考生根据要求作 答。 （一）必做题：共 60 分。 17. 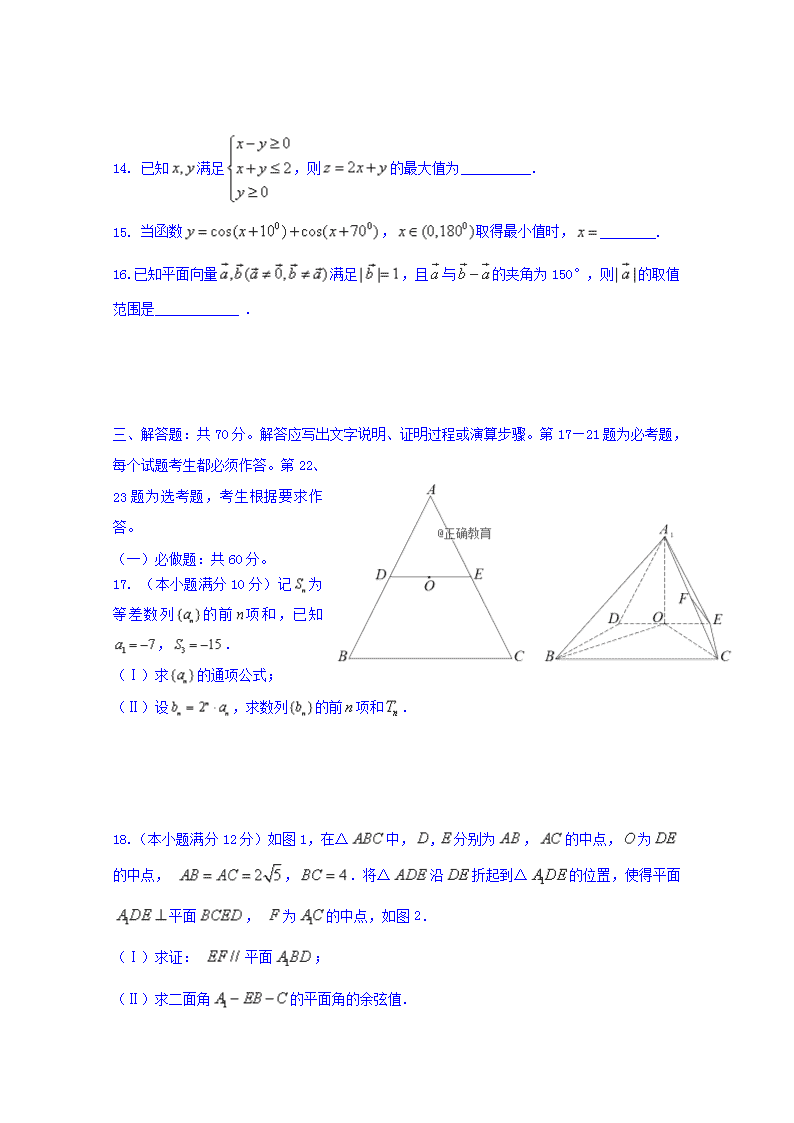（本小题满分 10 分）记 为 等差数列 的前 项和，已知 ， ． （Ⅰ）求 的通项公式； （Ⅱ）设 ，求数列 的前 项和 ． 18.（本小题满分 12 分）如图 1，在△ 中， , 分别为 ， 的中点， 为 的中点， ， ．将△ 沿 折起到△ 的位置，使得平面 平面 ， 为 的中点，如图 2． （Ⅰ）求证： 平面 ； （Ⅱ）求二面角 的平面角的余弦值. ,x y    ≥ ≤+ ≥− 0 2 0 y yx yx yxz += 2 0 0cos( 10 ) cos( 70 )y x x= + + + 0(0,180 )x∈ x = , ( 0, )a b a b a≠ ≠    | | 1b = a b a−  | |a nS { }na n 1 7a = − 3 15S = − { }na 2n n nb a= ⋅ { }nb n nT ABC D E AB AC O DE 2 5AB AC= = 4BC = ADE DE 1A DE 1A DE ⊥ BCED F 1AC //EF 1A BD 1A EB C− − 图 1 图 2 19. （本小题满分 12 分）生蚝即牡蛎 是所有食物中含锌最丰富的，在亚热带、热带 沿海都适宜生蚝的养殖，我国分布很广，北起鸭绿江，南至海南岛，沿海皆可产生蚝，生蚝 乃软体有壳，衣服寄生的动物，咸淡水交界所产尤为肥美，因此生蚝称为了一年四季不可或 缺的一类美食，某饭店从某水产养殖厂购进一批生蚝，并随机抽取了 40 只统计质量，得到结 果如下表所示： （Ⅰ）若购进这批生蚝 ，且同一组数据用该组区间的中点值代表，试估计这批生蚝的 数量（所得结果保留整数）； （Ⅱ）以频率估计概率，若在本次购买的生蚝中随机挑选 4 个，记质量在 间的生蚝的 个数为 ，求 的分布列及数学期望. 20.（本小题满分 12 分）已知抛物线 的焦点为 ， 为抛物线 上异于 原点的任意一点，过点 的直线 交抛物线 于另一点 ，交 轴的正半轴于点 ，且有 .当点 的横坐标为 3 时， 为正三角形. （Ⅰ）求抛物线 的方程； （Ⅱ）若直线 ，且 和抛物线 有且只有一个公共点 ，试问直线 （ 为抛物线 上异于原点的任意一点）是否过定点，若过定点，求出定点坐标；若不过定点，请说明理由. 21. （本小题满分 12 分）设函数 ( )oyster 500kg [5,25) X X 2: 2 ( 0)C y px p= > F A C A l C B x D | | | |FA FD= A ADF∆ C 1 //l l 1l C E AE A C 2( ) (1 ) ( 1)xh x x e a x= − − + （Ⅰ）若函数 在点 处的切线方程为 ，求实数 与 的值； （Ⅱ）若函数 有两个零点 ，求实数 的取值范围，并证明： . （二）选做题：共 10 分。请考生在第 22、23 题中任选一题作答，如果多做，则按所做的第 一题计分。 22.（本小题满分 10 分）[选修 4—4：坐标系与参数方程] 在直角坐标系中，已知曲线 的参数方程为 为参数 以原点为极点 x 轴正 半轴为极轴建立极坐标系，直线 的极坐标方程为： ，直线 的极坐标方程为 ． （Ⅰ）写出曲线 的极坐标方程，并指出它是何种曲线； （Ⅱ）设 与曲线 交于 两点， 与曲线 交于 两点，求四边形 面积的取 值范围． 23．（本题满分 10 分）选修 4—5：不等式选讲 设函数 ． （Ⅰ）当 时，求不等式 的解集； （Ⅱ）若 对 恒成立，求 的取值范围。 ( )h x (0, (0))h 2y kx= + k a ( )h x 1 2,x x a 1 2 0x x+ < M 1 2cos 1 2sin x y β β = +  = + β( ), 1l θ α= 2l = + 2 πθ α M 1l M ,A C 2l M ,B D ABCD ( ) | 1| | | ( )f x x x a a= − + − ∈R 4a = ( ) 5f x ≥ ( ) 4f x ≥ x∈R a 数学试题（理工类） 参考答案 一、 选择题： 1～5, DBCDC 6～10, ABCAD 11～12,DA 二、 填空题： 13, 1 14， 4 15， 16， 三、 解答题: 17、解析（1） ；（2）错位相减法， 18.解：（Ⅰ）取线段 的中点 ，连接 ， ． 因为在△ 中， ， 分别为 ， 的中点，所以 ， ． 因为 ， 分别为 ， 的中点，所以 ， ， 所以 ， ，所以 四边形 为平行四边形，所以 ． 因为 平面 ， 平面 ，所以 平面 ．……… 6 分 （Ⅱ）分别以 为 轴建立空间直角坐标系，则面 的法向量 , , , ,则 ,设面 的法向量 ，则 ，解得 ，所以， ，所以 所以二面角 的平面角的余弦值 .………… 12 分 19.解：（1）由表中的数据可以估算妹纸生蚝的质量为 ， 0140 (0,2] 2 9na n= − 1(2 11) 2 22n nT n += − ⋅ + 1A B H HD HF ABC D E AB AC //DE BC 1 2DE BC= H F 1A B 1AC //HF BC 1 2HF BC= //HF DE HF DE= DEFH //EF HD EF ⊄ 1A BD HD ⊂ 1A BD //EF 1A BD 1, ,OB OC OA , ,x y z BEC 1 1 (0,0,2)n OA= =  1 (0,0,2)A = (2 2,0,0)B (0,1,0)E 1 (2 2,0,2)A B = 1 (0,1, 2)A E = − 1A BE 2 ( , , )n x y z= 2 2 2 0 2 0 x z y z  − = − = 2 2 2 1 x y z  =  =  =  2 2( ,2,1)2n = 1 2 1 2 2 22cos 11| || | 112 2 n n n n θ ⋅= = = ×     1A EB C− − 22 11 − 1 (6 10 10 20 12 30 8 40 4 50) 28.540 g× + × + × + × + × = 所以购进 ，生蚝的数列均为 （只）； （2）由表中数据知，任意挑选一只，质量在 间的概率为 ， 的可能取值为 ，则 , , 所以 的分布列为 所以 20.解：（1）由题意知 ，设 ，则 的中点为 ， 因为 ，由抛物线的定义知： ，解得 或 （舍去）， 由 ，解得 ，所以抛物线 的方程为 . （2）由（1）知 ，设 ， ，因为 ，则 ，由 得 ，故 ， 故直线 的斜率为 ，因为直线 和直线 平行， 故可设直线 的方程为 ， 代入抛物线方程得 ， 由题意知 ，得 . 设 ，则 ， ， 当 时， ， 可得直线 的方程为 ， 500kg 500000 28.5 17554÷ ≈ [5,25) 2 5P = X 0,1,2,3,4 4 1 1 3 4 3 81 2 3 216( 0) ( ) , ( 1) ( ) ( )5 625 5 5 625P X P X C= = = = = = 2 2 2 3 3 1 4 4 4 2 3 216 2 3 96 2 16( 2) ( ) ( ) , ( 3) ( ) ( ) , ( 4) ( )5 5 625 5 5 625 5 625P X C P X C P X= = = = = = = = = X ( ) 216 96 16 83 3 4625 625 625 5E X = × + × + × = ( ,0)2 pF ( ,0)( 0)D t t > FD 2( ,0)4 p t+ | | | |FA FD= 3 | |2 2 p pt+ = − 3t p= + 3t = − 2 34 p t+ = 2p = C 2 4y x= (1,0)F 0 0 0( , )( 0)A x y x > ( ,0)( 0)D DD x x > | | | |FA FD= 0| 1| 1Dx x− = + 0Dx > 0 2Dx x= + 0( 2,0)D x + AB 0 2AB yk = − 1l AB 1l 0 2 yy x b= − + 2 0 0 8 8 0by yy y + − = 2 0 0 64 32 0b y y ∆ = + = 0 2b y = − ( , )E EE x y 0 4 Ey y = − 2 0 4 Ex y = 2 0 4y ≠ 0 0 2 0 0 4 4 E AE E y y yk x x y −= =− − AE 0 0 02 0 4 ( )4 yy y x xy − = −− 由 ，整理可得 ， 所以直线 恒过点 ， 当 时，直线 的方程为 ，过点 ， 所以直线 恒过定点 . 21.解：（1）因为 ，所以 又因为 ，所以 ，即 ……3 分 （2）因为 ，所以 ，令 ， 则 ， 令 ，解得 ，令 ，解得 ， 则函数 在 上单调递增，在 上单调递 减，所以 ， 又当 时， ，当 时， ， 画出函数 的图象，要使函数 的图象与 有两个不同的交点，则 ，即 实数的取值范围为 .……8 分 由上知， ，不妨设 ，则 ， 要证 ，只需证 ，因为 ，且函数 在 上单调递 减，所以只需证 ，由 ，所以只需 ， 即证 ，即证 对 恒成立， 令 ，则 因为 ，所以 ，所以 恒成立， 2 0 04y x= 0 2 0 4 ( 1)4 yy xy = −− AE (1,0)F 2 0 4y = AE 1x = (1,0)F AE (1,0)F ( ) 2xh x xe ax′ = − − (0) 0k h′= = (0) 1h a= − 1 2a− = 1a = − 2(1 ) xx e ax a− − = 2 (1 ) 1 xx ea x −= + ( ) 2 (1 ) 1 xx ef x x −= + ( ) 2 2 2 2 2 2 ( 2 3) [( 1) 2] ( 1) ( 1) x xx x x x xf x e ex x − − + − +′ = =+ + ( ) 0f x′ > 0x < ( ) 0f x′ < 0x > ( )f x ( ,0)−∞ (0, )+∞ ( ) ( )max 0 1f x f= = 1x < ( ) 0f x > 1x > ( ) 0f x < ( )f x ( )f x y a= 0 1a< < (0,1) 1 2x x≠ 1 2x x< 1 2( ,0), (0, )x x∈ −∞ ∈ +∞ 1 2 0x x+ < 2 1x x< − 2 1 (0, )x x− ∈ +∞ ( )f x (0, )+∞ ( ) ( )2 1f x f x> − ( ) ( )2 1f x f x= ( ) ( )1 1f x f x> − 1 11 1 2 2 1 1 1 1 1 1 x xx xe ex x −− +>+ + (1 ) (1 ) 0x xx e x e−− − + > ( ,0)x∈ −∞ ( ) (1 ) (1 ) , ( ,0)x xg x x e x e x−= − − + ∈ −∞ ( ) ( )xg x x e e−′ = − ( ,0)x∈ −∞ 0xe e− − > ( ) 0g x′ < 则函数 在 的单调递减，所以 ， 综上所述 .……12 分 22.解：（Ⅰ）由 （ 为参数）消去参数 得： ， 将曲线 的方程化成极坐标方程得： ， ∴曲线 是以 为圆心 为半径的圆． ……………… 5 分 （Ⅱ）设 ，由 与圆 M 联立方程可得 ， ∵O，A，C 三点共线，则 ①， ∴用 代替 可得 , ． ……………… 10 分 23．（1） 等价于 或 或 ， 解得 或 。 故不等式 的解集为 。 （2）因为： ， 所以： 。 由题意得： ， 解得 或 。 ( )g x ( ,0)x∈ −∞ ( ) ( )0 0g x g> = 1 2 0x x+ < 1 2cos 1 2sin x y β β = +  = + β β 2 2( 1) ( 1) 4x y− + − = M 2 -2 (sin cos ) 2 0ρ ρ θ θ+ − = M )1,1( ,2 1 2| | ,| |OA OCρ ρ= = 1l 2 2 (sin cos ) 2 0ρ ρ α α− + − = 1 2 1 2+ =2(sin cos ) = 2ρ ρ α α ρ ρ∴ + ⋅ −， 2 1 2 1 2 1 2| | | | ( ) 4 12 4sin 2AC ρ ρ ρ ρ ρ ρ α= − = + − ⋅ = + + 2 πα α | | 12 4sin 2BD α= − 2 1 2 1 1, = |AC||BD|= (144 16sin 2 )2 2ABCDl l S α⊥ ∴ ⋅ − 四边形 2sin 2 [0,1] [4 2,6]ABCDSα ∈ ∴ ∈ 四边形 | 1| | 4 | 5x x− + − ≥ 1 2 5 5 x x < − + ≥ 1 4 3 5 x≤ ≤  ≥ 4 2 5 5 x x >  − ≥ 0x ≤ 5x ≥ ( ) 5f x ≥ { | 0 5}x x x≤ ≥或 ( ) | 1| | | | ( 1) ( ) | 1|f x x x a x x a a= − + − ≥ − − − = − min( ) | 1|f x a= − | 1| 4a − ≥ 3a ≤ − 5a ≥