- 446.17 KB
- 2024-03-10 发布
2018年高考数学讲练测【新课标版理】【练】选修4-4 坐标系和参数方程
第01节 坐标系
A基础巩固训练
1. 在极坐标系中,若点,则的面积为 ( )
A. B. C. D.
【答案】C
【解析】的面积为 ,选C.
2. 【2018北京西城高三上期中】极坐标方程和参数方程(为参数)所表示的图形分别是( ).
A. 直线、直线 B. 圆、圆 C. 直线、圆 D. 圆、直线
【答案】D
3. 若以直角坐标系的原点为极点,轴的非负半轴为极轴建立极坐标系,则线段的极坐标为( )
A. B. C. D.
【答案】A
4.【2018湖北华师一附中调研】圆锥曲线的准线方程是 ( )
A. B. C. D.
【答案】D
【解析】将化成,即,即该圆锥曲线的直角坐标方程为,其准线方程为,即;故选D.
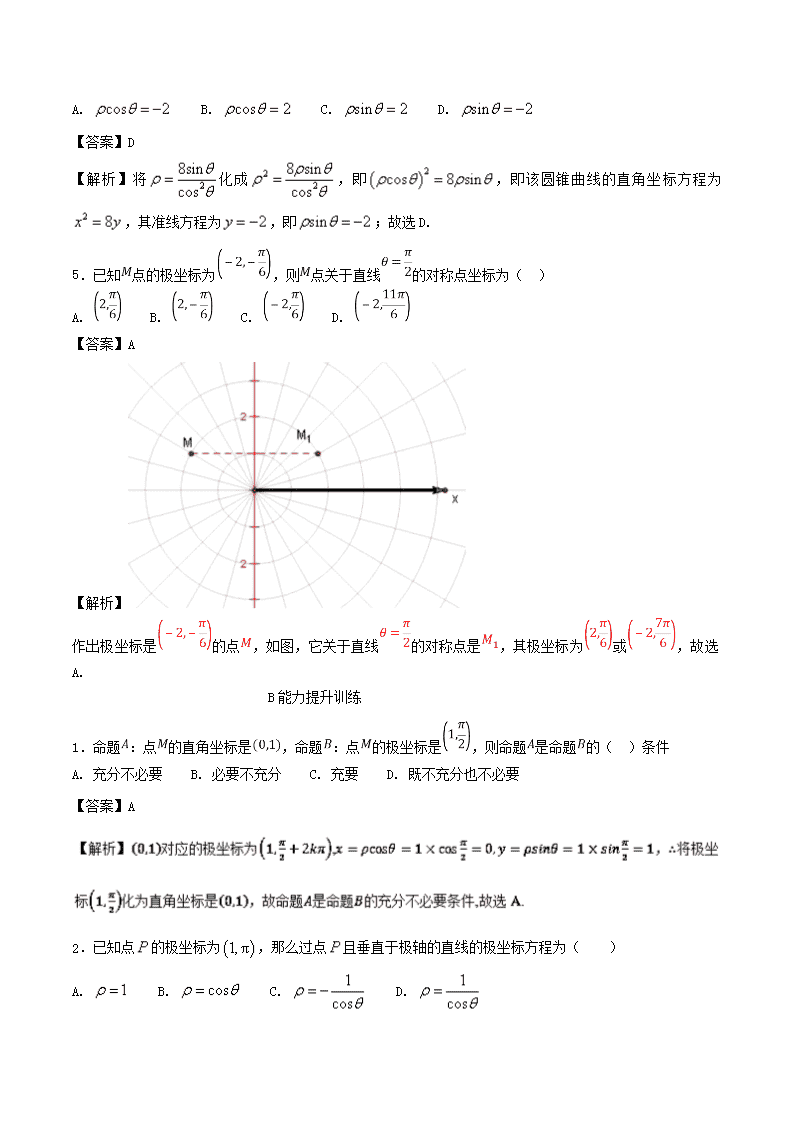
5.已知点的极坐标为,则点关于直线的对称点坐标为( )
A. B. C. D.
【答案】A
【解析】
作出极坐标是的点,如图,它关于直线的对称点是,其极坐标为或,故选A.
B能力提升训练
1.命题:点的直角坐标是,命题:点的极坐标是,则命题是命题的( )条件
A. 充分不必要 B. 必要不充分 C. 充要 D. 既不充分也不必要
【答案】A
2.已知点的极坐标为,那么过点且垂直于极轴的直线的极坐标方程为( )
A. B. C. D.
【答案】C
【解析】由极坐标,设直线上任取一点,由图形可知 ,选C.
3.极坐标方程 r=cos表示的曲线是( ).
A. 圆 B. 椭圆 C. 抛物线 D. 双曲线
【答案】A
【解析】因为,所以方程 r=cos ,即,故该方程表示圆心为,半径是的圆,应选答案A。
4.在极坐标系中,设圆与直线交于两点,则以线段为直径的圆的极坐标方程为( )
A. B.
C. D.
【答案】A
【解析】试题分析:以极点为坐标原点,极轴为轴的正半轴,建立直角坐标系,则由题意,得圆的直角坐标方程,直线的直角坐标方程.由,解得或
5.在极坐标系中,曲线与直线交点的极坐标为_______________
【答案】
C 思维拓展训练
1.【2018云南昆明一中模拟】极坐标系中, 为极点,半径为2的圆的圆心坐标为.
(1)求圆的极坐标方程;
(2)设直角坐标系的原点与极点重合, 轴非负关轴与极轴重合,直线的参数方程为(为参数),由直线上的点向圆引切线,求切线长的最小值.
【解析】(Ⅰ)设是圆上任意一点,
如图,连接,并延长与圆交于点,
当点异于, 时,连接、,
直角△中, ,
即,
当点与, 重合时,也满足上式,所求圆的极坐标方程为.
(Ⅱ)直线的普通方程为,圆心到直线的距离为,
,所以直线与圆相离,
故切线长的最小值为.
2.【2018四川绵阳市模拟】在直角坐标系中,曲线的参数方程是(
为参数),以坐标原点为极点,轴正半轴为极轴,建立极坐标系.
(1)求曲线的极坐标方程;
(2)设,,若与曲线分别交于异于原点的两点,求的面积.
3.在直角坐标系中,圆的参数方程为(参数),以为极点, 轴的非负半轴为极轴建立极坐标系,直线的极坐标方程为.
(1)求的极坐标方程;
(2)射线与圆的交点为,与直线的交点为,求的范围.
【解析】(1)圆的普通方程是,又,
所以圆的极坐标方程是.
(2)设,则有 ,
设,且直线的方程是,则有
所以
因为,所以.
4.【2018甘肃张掖市模拟】在直角坐标系中,已知圆: (为参数),点在直线: 上,以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系.
(1)求圆和直线的极坐标方程;
(2)射线交圆于,点在射线上,且满足,求点轨迹的极坐标方程.
【解析】
(1)圆的极坐标方程,直线的极坐标方程=.
(2)设的极坐标分别为,因为
又因为,即
,
.
5.【2018湖南师大附中模拟】已知在平面直角坐标系中, 为坐标原点,曲线: (为参数),在以平面直角坐标系的原点为极点, 轴的正半轴为极轴,取相同单位长度的极坐标系,直线: .
(Ⅰ)求曲线的普通方程和直线的直角坐标方程;
(Ⅱ)曲线上恰好存在三个不同的点到直线的距离相等,分别求出这三个点的极坐标.
(Ⅱ)∵圆的圆心半径为2,圆心到直线的距离为1,
∴这三个点在平行直线与上,如图:直线与与的距离为1.
: , : .
可得
两个交点;
解得,
这三个点的极坐标分别为: 、.