高考理科数学专题复习练习2.5对数与对数函数 3页

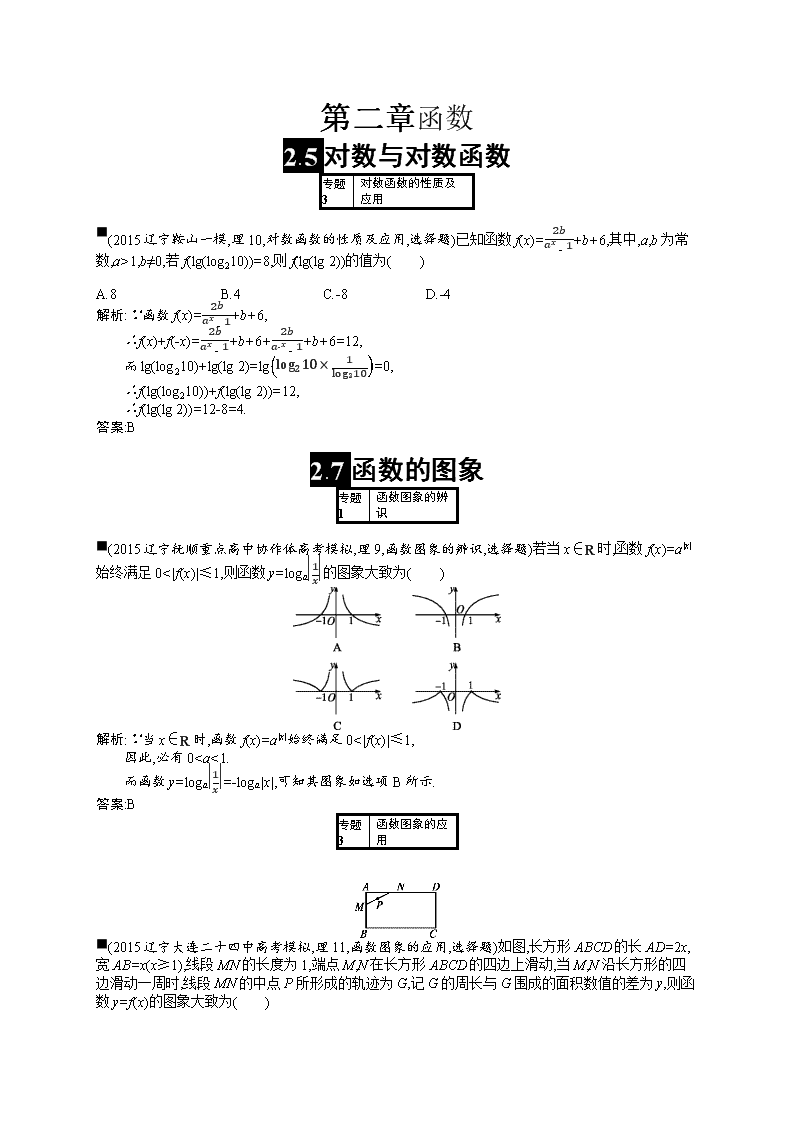
第二章函数 ‎2.5对数与对数函数 专题3‎ 对数函数的性质及应用 ‎■(2015辽宁鞍山一模,理10,对数函数的性质及应用,选择题)已知函数f(x)=‎2bax‎-1‎+b+6,其中,a,b为常数,a>1,b≠0,若f(lg(log210))=8,则f(lg(lg 2))的值为(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A.8 B.4 C.-8 D.-4‎ 解析:∵函数f(x)=‎2bax‎-1‎+b+6,‎ ‎∴f(x)+f(-x)=‎2bax‎-1‎+b+6+‎2ba‎-x‎-1‎+b+6=12,‎ 而lg(log210)+lg(lg 2)=lglog‎2‎10×‎‎1‎log‎2‎10‎=0,‎ ‎∴f(lg(log210))+f(lg(lg 2))=12,‎ ‎∴f(lg(lg 2))=12-8=4.‎ 答案:B ‎2.7函数的图象 专题1‎ 函数图象的辨识 ‎■(2015辽宁抚顺重点高中协作体高考模拟,理9,函数图象的辨识,选择题)若当x∈R时,函数f(x)=a|x|始终满足0<|f(x)|≤1,则函数y=loga‎1‎x的图象大致为(　　)‎ 解析:∵当x∈R时,函数f(x)=a|x|始终满足0<|f(x)|≤1,‎ 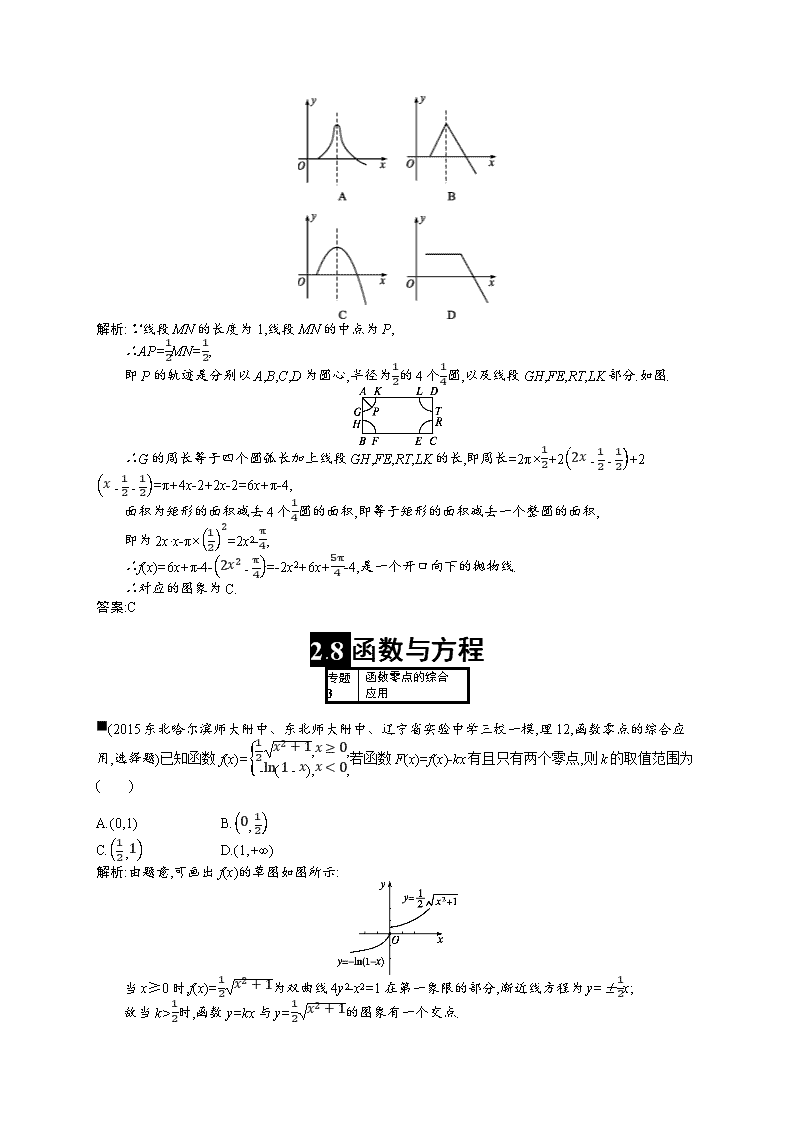因此,必有0‎1‎‎2‎时,函数y=kx与y=‎1‎‎2‎x‎2‎‎+1‎的图象有一个交点.‎ 当k=1时,由y=-ln(1-x),可得y'=‎1‎‎1-x=1可得x=0,即y=-ln(1-x)在x=0处的切线方程为y=x,‎ 故当k<1时,y=kx与y=-ln(1-x)的图象有一个交点.‎ 故当k∈‎1‎‎2‎‎,1‎时,函数F(x)=f(x)-kx有且只有两个零点.‎ 答案:C